(a) Derive the experience for the forest acting between two long parallel current carrying conductors. Hence , defined 1 A current .
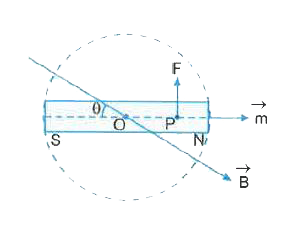
(b) A bar magnet of dipole moment 3 A m2 . rests with its centre on a frictionless pivot. A force F is applied at right angles to the axis of the magnet , 10 cm from the pivot . It is observed that an external magnetic field of 0.25 T is required to hold the magnet in equilibrium at an angle of 30∘ with the field.
Calculate the value of F.
How will the equilibrium be effected if F is withdrawn?
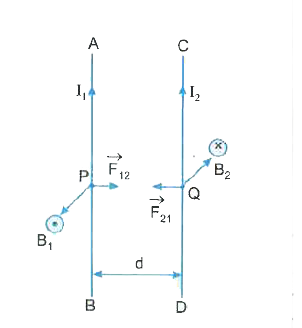
(a) Consider two straight , parallel , long current carrying conductors AB and CD carrying currents I1andI2. respectively in same direction and let these be separated by a distance d . Now magnetic field B1 developed at a point Q on 2nd conductor due to current I1 flowing in Ist conductor is
B1=μ0I12πd
As per right hand rule B1 is acting to the plane of the paper pointing inward . Thus, conductor CD carrying I2 is magnetic field which is perpendicular to its length . Therefore , force experienced by 2nd conductor CD due to B1
F21=B1I2l
Where l = length of the 2nd conductor and force per unit length
or F21=u0I12πdI2l=μ0I1I2l2πd
and force per unit length
F21l=μ0I1I22πd=μ04π.2I1I2d
The force F21 in accordance with Fleming.s left hand rules is directed towards the conductor AB. In the same way, it is found that force experienced per unit length of wire AB is
F12l=μ04π.2I1I2d
and is directed towards CD.
If I1=I2A and d = 1, then F12ρ=μ04π×2×1×11=μ02π=2×10−7Nm−1.
Hence, SI base unit of current i.e. , ampere is defined as the value of that steady current which when maintained in each of the two very long straight , parallel conductors of negligible cross-section and placed 1 m apart in vacuum would produce one each of these conductors a force equal to 2×10−7Nm−1 .
(b) Here dipole moment of bar magnet m = 3 A m2 , external magnetic field B = 0.25 T , θ=30∘ . Let a force F be applied on the magnet at a point P situated at a distance d = 10 cm (or 0.1m) from the centre ( pivot point) O at right angles to the axis of magnet as shown.
Since magnet is in equilibrium , net torque acting on the magnet must be zero . Hence
mBsinθ=F×d
⇒F=mBsinθd=3×0.25×sin30∘0.1=3.75N
the force F is withdrawn then under the influence of torque τ=mBsinθ will oscillate to and from about the its equilibrium position along the magnetic field.
Topper's Solved these Questions
- CBSE EXAMINATION PAPER 2020 (SOLVED) BOOK - U-LIKE SERIESCHAPTER - CBSE EXAMINATION PAPER 2020 (SOLVED) EXERCISE - SECTION - C
7 Videos
- CBSE EXAMINATION PAPER 2020 (SOLVED)BOOK - U-LIKE SERIESCHAPTER - CBSE EXAMINATION PAPER 2020 (SOLVED)EXERCISE - SECTION D
11 Videos
- CBSE SAMPLE QUESTION PAPER 2019-20 (SOLVED)BOOK - U-LIKE SERIESCHAPTER - CBSE SAMPLE QUESTION PAPER 2019-20 (SOLVED)EXERCISE - SECTION D
6 Videos
Similar Questions
An infinitely thin straight wire has uniform linear charge density λ . Obtain the expression. For the electric field (E) at a point lying at a distance x from the wire, using Gauss' law.
(b) Show graphically the variation of this electric field E as a function of distance x from the wire .
View SolutionDefine the term 'focal length ofa mirror. With the help of a ray diagram, obtain the relation between its focal length and radius of curvature.
View Solution(a) Using Gauss's law, derive expression for intensity of electric field at any point near the infinitely long straight uniformly charged wire.
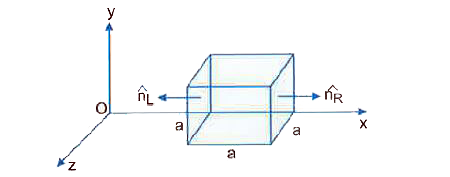
(b) The electric field components in the following figure are Ex=αx,Ey=0,Ez=0, in which α=400N/Cm. Calculate (i) the electric flux through the cube, and (ii) the charge within the cube assume that a=0.1m.
View SolutionA bar magnet with poles 25cm apart and of strength 14.4amp−m rests with centre on a frictionless pivot. It is held in equilibrium aat an angle of 60∘ with respect to a uniform magnetic field of induction 0.25Wb/m2,byapply∈gaforceFatright∠s→itsaξsatap∮12 cmomπvot.Calca––teF.WˆwillhappeniftheforceF is removed?
View SolutionDerive an expression for the force between two long parallel current carrying conductors. Use this expression to define SI unit of current.
View SolutionA bar magnetic with poles 25cm apart and pole strength 14*4A.m rests with its centre on a frictionless pivot. It is held in equilibrium at 60^@ to a uniform magnetic field of induction 0*25T by applying a force F at right angles to its axis, 10cm from the pivot. Calculate the value of F. What will happen if the force is removed?
View SolutionA bar magnet with poles 25.0 cm apart and of pole strength 14.4 Am rests with its centre on a friction less point. It is held in equilibrium at 60^(@) to a uniform magnetic field of induction 0.25 T by applying a formce F at right angle to the axis, 12 cm from its pivot. The magnitude of the force is
View SolutionA bar magnet with its poles 25 cm apart and of pole strength 24.0 A-m rests with its centre on a frictionless pivot. A force F is applied on the magnet at a distance of 12 cm from the pivot, so that it is held in equilibrium at an angle of 30^(@) with respect to a magnetic field of induction 0.25 T. The value of force F is
View SolutionA pivoted small magnetic needle of moment m is placed at a distance r along the axis of a short bar magnet of moment M. Find the force on the pivot of the needle.
View SolutionDerive an expression for the force acting between two very long parallel current-carrying conductors and hence define the Ampere.
View SolutionNo force acts on a current carrying conductor in a magnetic field when angle between current and magnetic field is
View SolutionA current carrying conductor placed in a magnetic field experiences maximum force when angle between current and magnetic field is :
View SolutionA bar magnet with poles 25.0 cm apart and of pole strength 14.4 Am rests with its centre on a frictionless point. It is held in equilibrium at 60∘ to a uniform magnetic field of induction 0.25T by applying a force F at right angle to the axes, 12 cm from its pivot. The magnitude of the force is :
View SolutionDerive an expression for the force between two long parallel current carrying conductors. Use this expression to define SI unit of current.
View SolutionMagnetic Force on a Current carrying conductor#!#Magnetic Dipole Moment
View Solution
