A force 2¯i+¯j−¯k Newton acts on a body which is initially at rest . At the end of 20 seconds the velocity of the body is 4¯i+2¯j−2¯k m/s . What is the mass of the body ?
To find the mass of the body given the force acting on it, we can use Newton's second law of motion, which states that the force acting on an object is equal to the mass of the object multiplied by its acceleration (F = m * a).
1. Identify the Given Values:
- Force →F=2^i+^j−^k Newton
- Initial velocity →u=0 (body is initially at rest)
- Final velocity →v=4^i+2^j−2^k m/s
- Time t=20 seconds
2. Calculate the Acceleration:
- We can use the kinematic equation:
→v=→u+→at
- Since →u=0, the equation simplifies to:
→v=→at
- Rearranging gives:
→a=→vt
- Substituting the values:
→a=4^i+2^j−2^k20
- This simplifies to:
→a=15^i+110^j−110^k(m/s2)
3. Calculate the Magnitude of the Acceleration:
- The magnitude of →a is given by:
|→a|=√(15)2+(110)2+(−110)2
- Calculating:
|→a|=√125+1100+1100=√4100=210=15(m/s2)
4. Calculate the Magnitude of the Force:
- The magnitude of the force →F is:
|→F|=√(2)2+(1)2+(−1)2=√4+1+1=√6(N)
5. Apply Newton's Second Law:
- According to Newton's second law:
|→F|=m⋅|→a|
- Substituting the magnitudes:
√6=m⋅15
- Rearranging gives:
m=5√6(kg)
6. Final Calculation:
- To find the numerical value of the mass:
m=10(kg)
Conclusion:
The mass of the body is 10 kg.
- Force →F=2^i+^j−^k Newton
- Initial velocity →u=0 (body is initially at rest)
- Final velocity →v=4^i+2^j−2^k m/s
- Time t=20 seconds
- We can use the kinematic equation:
→v=→u+→at
- Since →u=0, the equation simplifies to:
→v=→at
- Rearranging gives:
→a=→vt
- Substituting the values:
→a=4^i+2^j−2^k20
- This simplifies to:
→a=15^i+110^j−110^k(m/s2)
- The magnitude of →a is given by:
|→a|=√(15)2+(110)2+(−110)2
- Calculating:
|→a|=√125+1100+1100=√4100=210=15(m/s2)
- The magnitude of the force →F is:
|→F|=√(2)2+(1)2+(−1)2=√4+1+1=√6(N)
- According to Newton's second law:
|→F|=m⋅|→a|
- Substituting the magnitudes:
√6=m⋅15
- Rearranging gives:
m=5√6(kg)
- To find the numerical value of the mass:
m=10(kg)
The mass of the body is 10 kg.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - NUMERICAL EXXERCISE (LEVEL -1)13videos
ELEMENTS OF VECTORS
- BOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - NUMERICAL EXXERCISE (LEVEL -2)21videos
ELEMENTS OF VECTORS
- BOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - SHORT ANSWER TYPE QUESTIONS10videos
ELEMENTS OF VECTORS
- BOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)5videos
ELECTROSTATICS
- BOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)10videos
GEOMETRICAL OPTICS
Similar Questions
Knowledge Check
- Question 1 - Select One
A force vector applied on a mass is represented as F=6i−8j+10k and acceleration with 1 m/s2. What will be the mass of the body ?
A10√2 kgB2√10 kgC10 kgD20 kg
At 0∘C the density of a gaseous oxide at 2 bar is same as that of nitrogen at 5 bar What is the molecular mass of the oxide ? .
View SolutionIdentify the locus of z if ¯z=¯a+r2z−a.
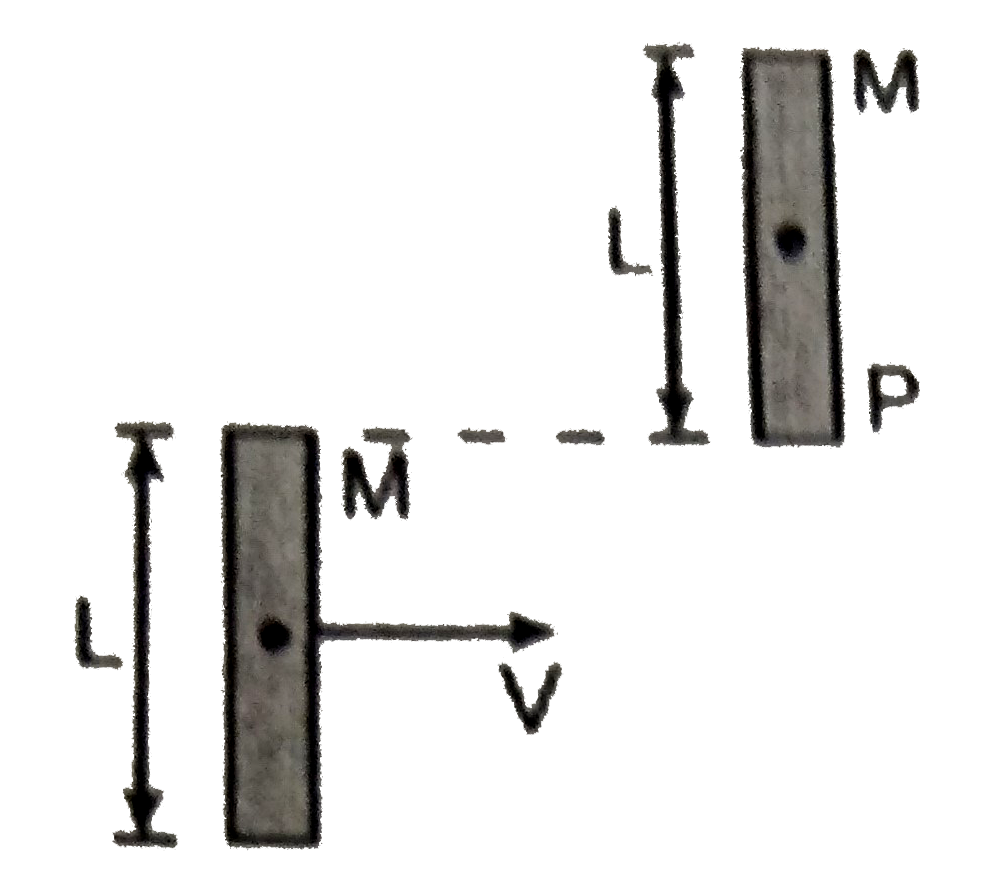
View SolutionA bar of mass M and length L is in pure traslatory motion with its of mass velocity V . It collides with and sticks to a second identical bar which is initially at rest . ( Assume that it bocomes one composite bar of length 2L). The angular velocity of the composite bar will be
 View Solution
View SolutionEvaluate :
2.¯5−0.¯¯¯¯35View SolutionEvaluate 3.¯2−0.¯¯¯¯16
View SolutionIf ¯¯¯X1and¯¯¯X2 are the means of two series such that ¯¯¯X1<¯¯¯X2and¯¯¯X is the mean of the combined series, then
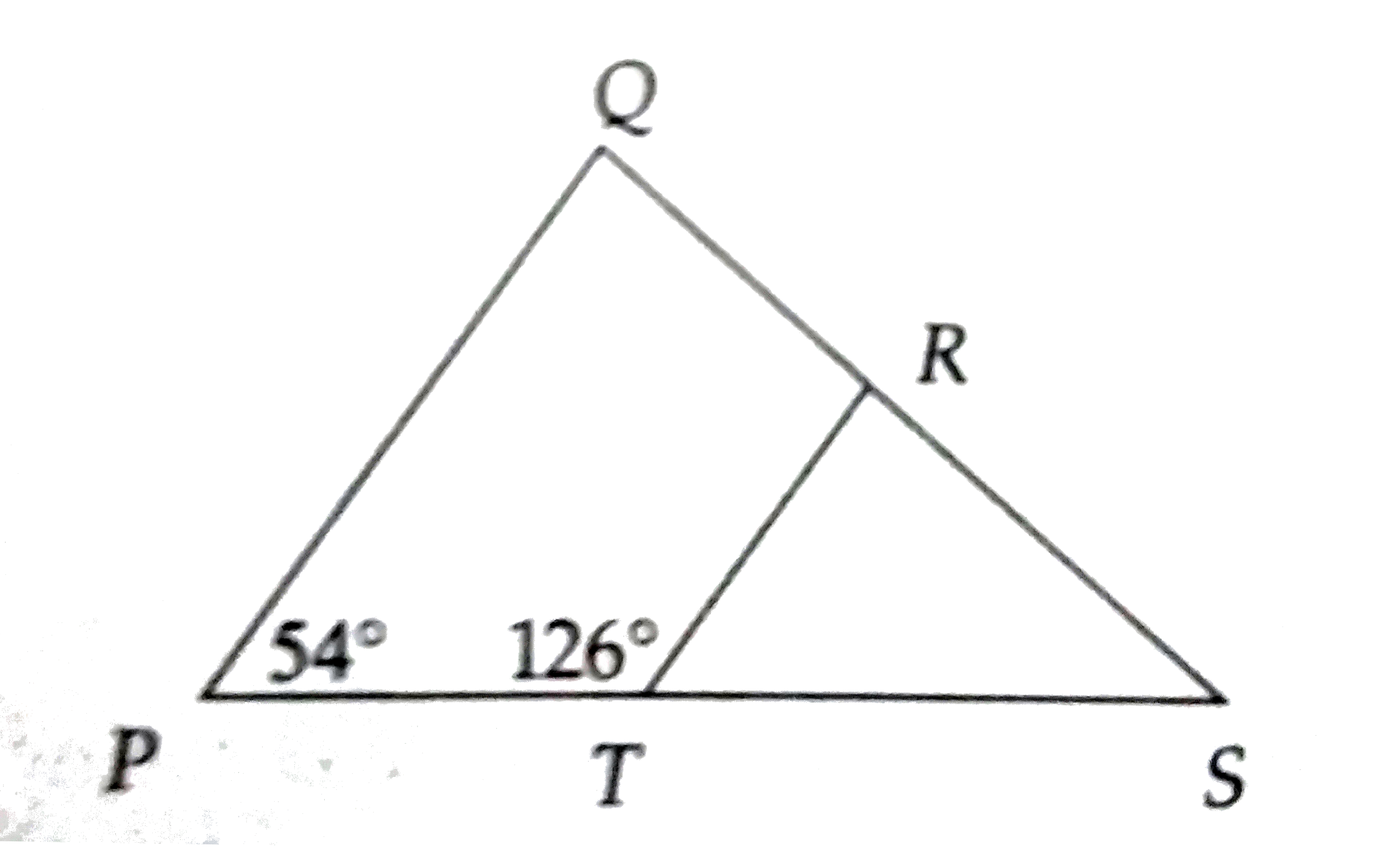
View Solution¯¯¯¯¯¯QR=¯¯¯¯¯RS. If the area of ΔRST is c2, what is the area of ΔQSP ?
 View Solution
View Solution