A force F is related to the position of a particle by the relation F=(10x2)N . Find the work done by the force when the particle moves from x=2m→x=4m.
563 J
560 J
5603 J
3560 J
The correct Answer is:C
To find the work done by the force when the particle moves from x=2m to x=4m, we can follow these steps:
Step 1: Understand the relationship between force and position
The force F is given by the relation:
F=10x2N
where x is the position in meters.
Step 2: Set up the work done integral
The work done W by a variable force is calculated using the integral:
W=∫x2x1Fdx
In this case, x1=2m and x2=4m. Thus, we can write:
W=∫4210x2dx
Step 3: Calculate the integral
Now, we need to evaluate the integral:
W=10∫42x2dx
To solve this integral, we use the power rule for integration:
∫xndx=xn+1n+1+C
For n=2:
∫x2dx=x33
Now substituting this back into our work equation:
W=10(x33)42
Step 4: Evaluate the definite integral
Now we evaluate the definite integral from 2 to 4:
W=10(433−233)
Calculating 43 and 23:
43=64and23=8
Substituting these values:
W=10(643−83)=10(64−83)=10(563)
Step 5: Final calculation
Now multiply:
W=5603J
Conclusion
Thus, the work done by the force when the particle moves from x=2m to x=4m is:
W=5603J
The force F is given by the relation:
F=10x2N
where x is the position in meters.
The work done W by a variable force is calculated using the integral:
W=∫x2x1Fdx
In this case, x1=2m and x2=4m. Thus, we can write:
W=∫4210x2dx
Now, we need to evaluate the integral:
W=10∫42x2dx
To solve this integral, we use the power rule for integration:
∫xndx=xn+1n+1+C
For n=2:
∫x2dx=x33
Now substituting this back into our work equation:
W=10(x33)42
Now we evaluate the definite integral from 2 to 4:
W=10(433−233)
Calculating 43 and 23:
43=64and23=8
Substituting these values:
W=10(643−83)=10(64−83)=10(563)
Now multiply:
W=5603J
Thus, the work done by the force when the particle moves from x=2m to x=4m is:
W=5603J
Topper's Solved these Questions
Similar Questions
Force acting on a particle varies with displacement as shown is Fig. Find the work done by this force on the particle from x=−4m to x = + 4m.
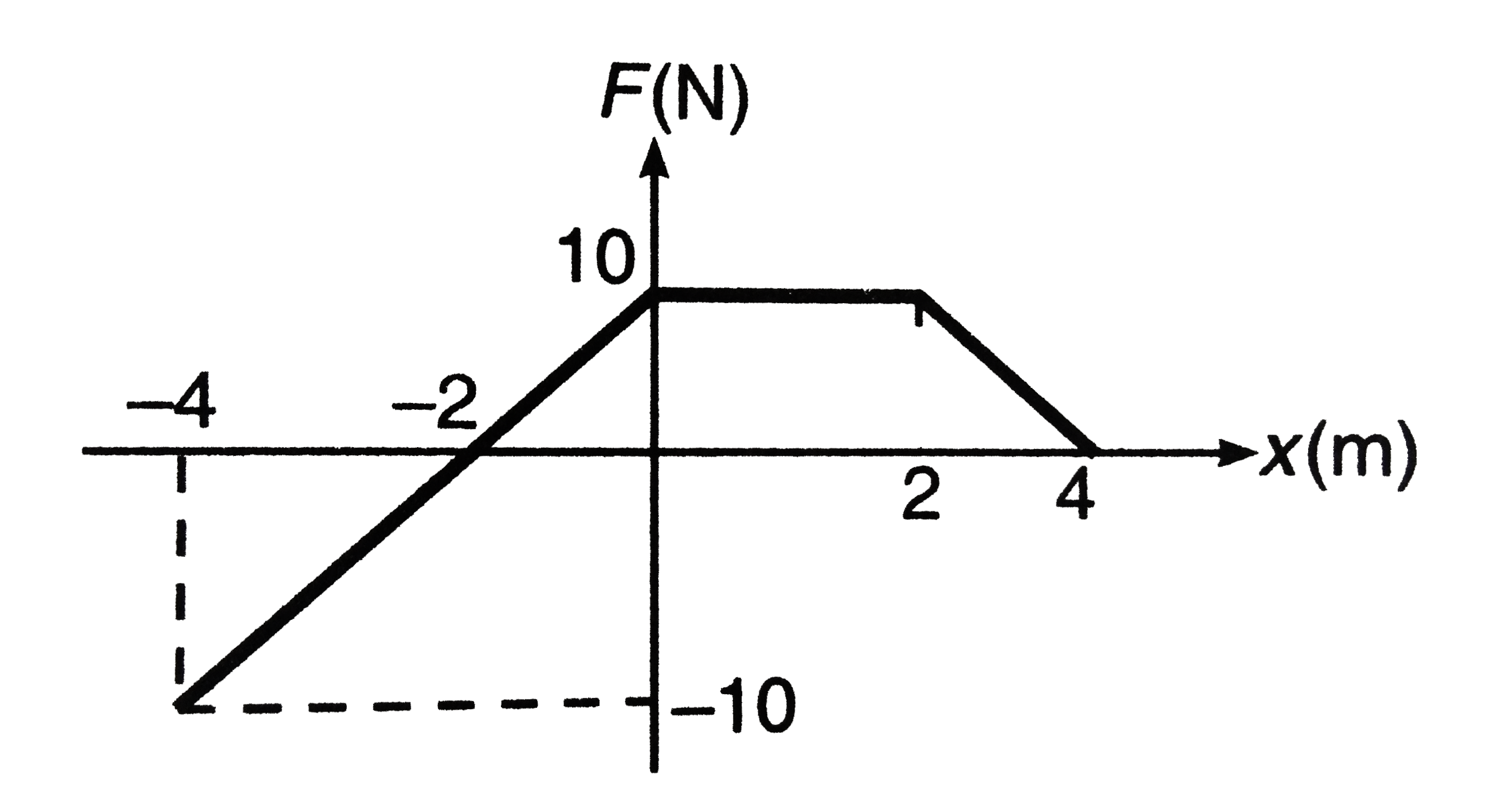 . View Solution
. View SolutionA variable force F acts along the x - axis given by F=(3x2)−2x+1N. The work done by the force when a particle of mass 100 g moves from x = 50 cm to x = 100 cm is
View SolutionA force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from
 View Solution
View SolutionA particle moves along x - axis under the action of a position dependent force F=(5x2−2x)N. Work done by force on the particle when it moves from origin to x = 3 m is
View SolutionA force (F) acting on a particle varies work done by a particle varies with the with the position x as shown in figure
 .
.
Find the work done by by force in displacing the particle from .
(a) x=−2m to x=0
(b) x=0 to x=2m..View SolutionA particle is subjected to a force Fx that varies withes position as shown in figure. Find the work done by the force on the body as it moves
(a) from x=10.0m to x=5.0m,
(b) from x=5.0m to x=10.0m,
(c ) from x=10.0m to x=15.0m,
(d) what is the total work done by the force over the distance x=0 to x=15.0?
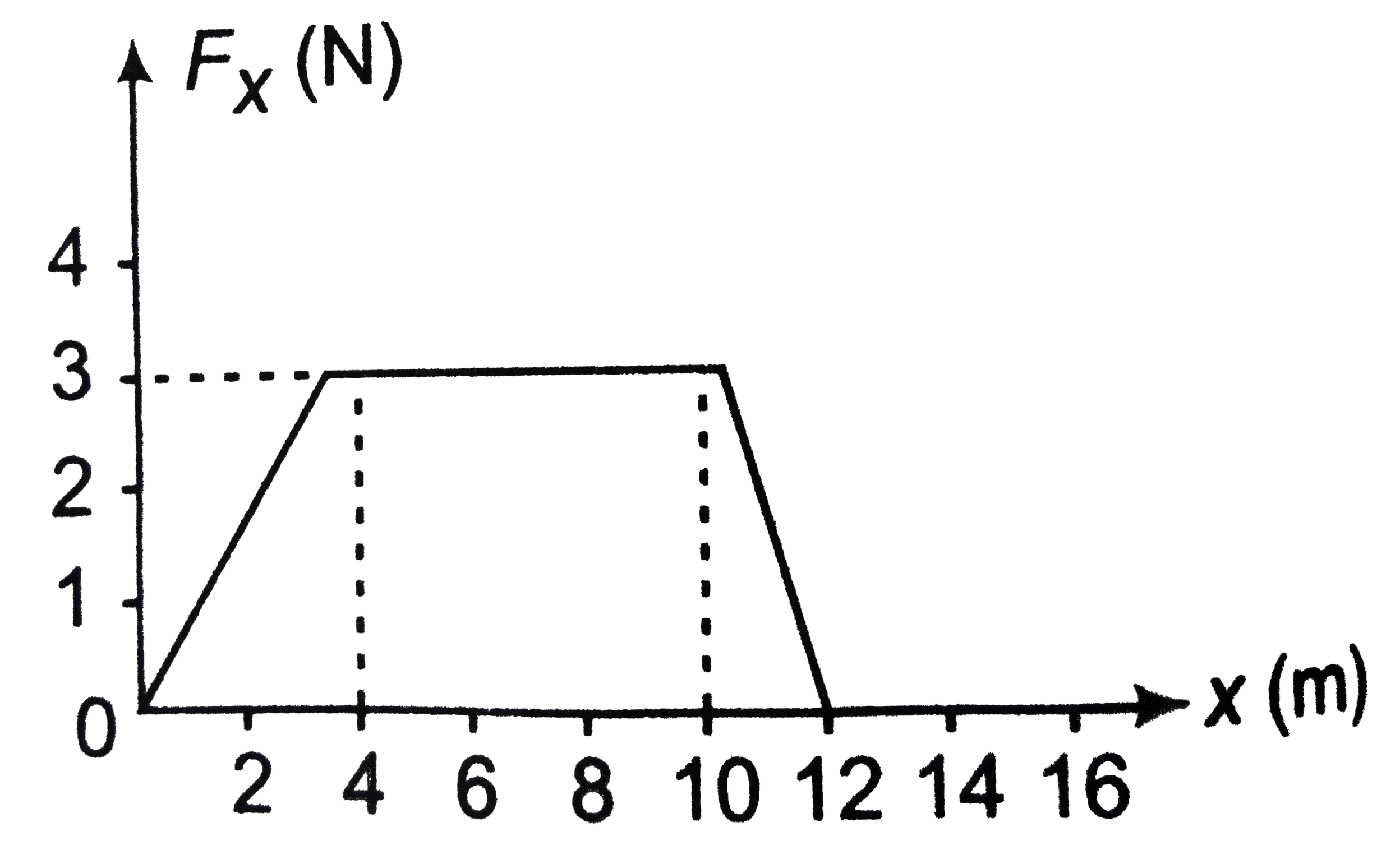 .View Solution
.View SolutionA force F=a+bx acts on a particle in the x-directioin, where a and b are constants. Find the work done by this force during a displacement form x=0→x=d.
View SolutionA force F=−kx2(x≠0) acts on a particle in x-direction. Find the work done by this force in displacing the particle from. x=+a to x=+2a. Where, k is a positive constant.
View SolutionA force F=−kx2(x≠0) acts on a particle in x-direction. Find the work done by this force in displacing the particle from. x=+a to x=2a. Here, k is a positive constant.
View SolutionA force F=(5+2x) acts on a particle in x direction where F is in newtown and x is meter. Find the work done by this force during displacement from x=0 to x=1m.
View Solution

