A frustum has been mounted with its axis vertical. It has a height h and radii of its upper and lower cross sections are R and r respectively. A particle is projected with horizontal velocity v0 along its upper brim. The particle spirals down the inner surface and leaves the lower face at point B. The inner wall of the frustum is smooth.
(a) Find the vertical component of velocity of the particle as it leaves the frustum at B.
(b) Find minimum value of h for which the particle will never come out of the frustum.
Take r=R2 for solving this part of the problem.
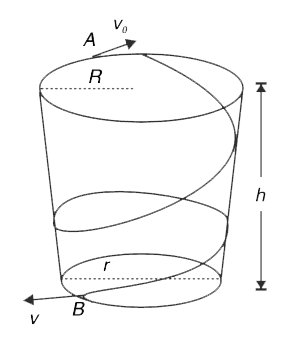
The correct Answer is:(a) √2gh−v20(R2r2−1)
(b) hmin=√32gv0
Topper's Solved these Questions
Similar Questions
Knowledge Check
A frustum of a cone has height 8 cm and radii of upper and lower circular surfaces are 22 cm and 16 cm respecticely. Its slant height is
A10 cmB8√5 cmC4√6 cmD6√3 cmA particle is projected horizontally with velocityV0=√2ga along the smooth inside surface of a fixed hollow hemisphere of inner radius 'a' at the level of the centre 'O'. The subsequent motion of the particle is confined between the horizontal planes one through the centre and the other at a depth h. Find the value of h:
A√32aB√3−13aC√5−12aD√52aThe curved surface area of a frustum of a cone is 21πcm2 . If the radii of its upper and lower circular surfaces are 5 cm and 7 cm respectively, then its total surface area is
A33πcm2B53πcm2C95πcm2D165πcm2
A solid frustum is of height 8 cm. If the radii of its lower and upper ends are 3 cm and 9 cm respectively, then its slant height is (a) 15 cm (b) 12 cm (c) 10 cm (d) 17 cm
View SolutionA solid frustum is of height 8 cm. If the radii of its lower and upper ends are 3 cm and 9 cm respectively, then its slant height is
(a) 15 cm
(b) 12 cm
(c) 10 cm
(d) 17 cm
View SolutionInner and outer radii of a spool are r and R respectively. A thread is wound over its inner surface and placed over a rough horizontal surface. Then:
 .
.
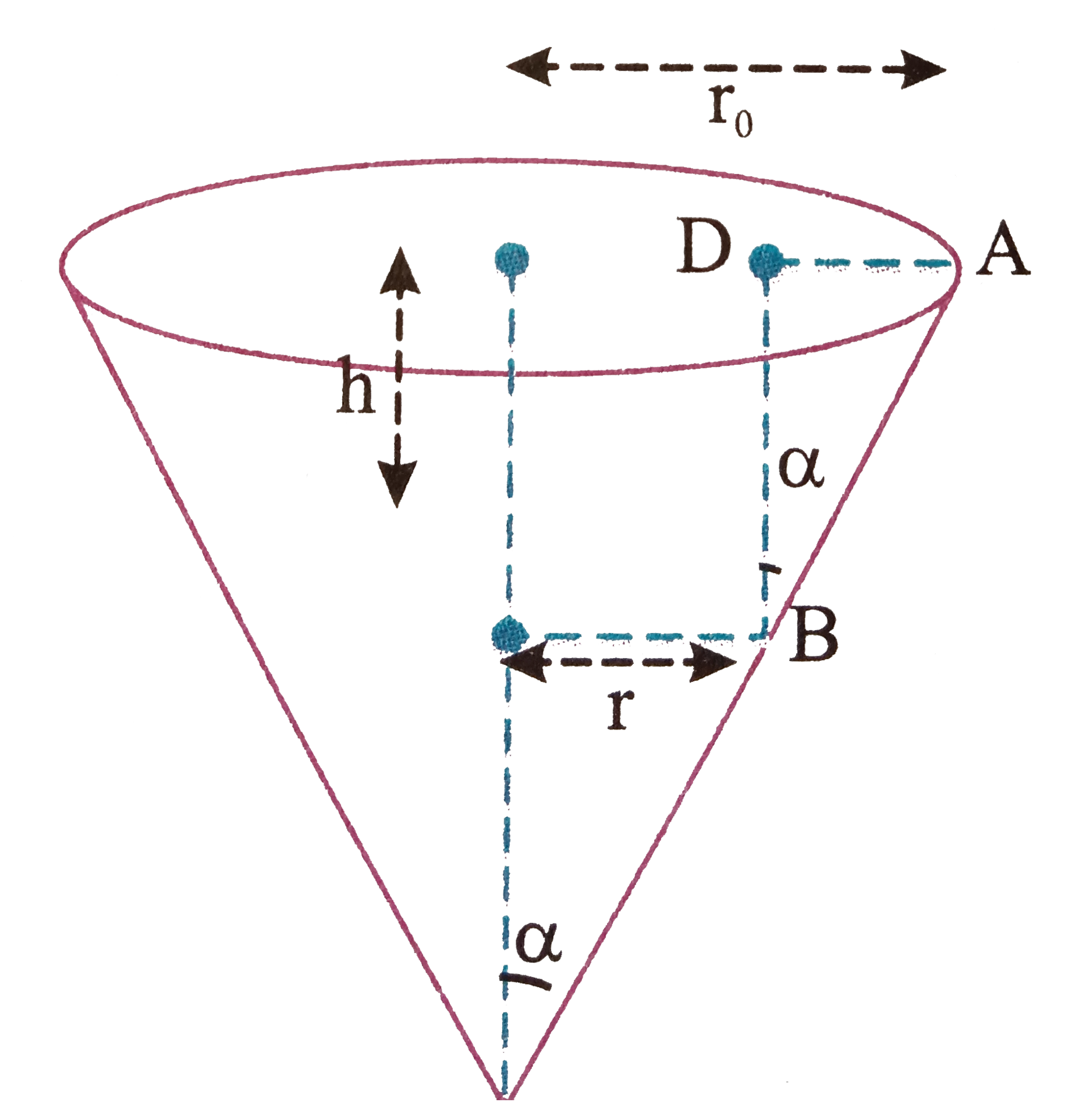
View SolutionA small particle of mass m is given an initial velocity v0 tangent to the horizontal rim of a smooth cone at a radius r0 from the vertical slides to point B, a vertical distance h below A and a distance r from the vertical centreline, its velocity v makes an angle θ with the horizontal tangent to the cone through B.
The minimum value of v0 for which particle will be moving in a horizontal circle of radius r0.
View Solution
A hollow vertical cylinder of radius r and height h has a smooth internal surface. A small particle is placed in contact with the inner side of the upper rim, at point A, and given a horizontal speed u, tangentical t the rim. it leaves the lower rim at point B, vertically below A. If n is an integer then
View Solution
