A glass rod having square cross-section is bent into the shape as shown in the figure. The radius of the inner semi-circle is R and width of the rod is d. Find the minimum value of d/R so that the light that enters at A will emerge at B. Refractive index of glass is μ=1.5

Minimum possible angle for internal reflection will be available for the ray coming along the inner edge as shown in figure.
For total internal reflection to take place at the point of incidence we can write the following condition :
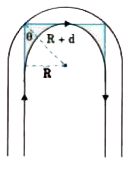
sinθ≥sinθC
⇒ sinθ≥11.5
⇒ RR+d≥11.5
⇒ 1.5R≥R+d
⇒ dR≤0.5
Hence maximum possible value for d/R is 0.5.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Revision Exercises (Very Short Answer Questions)
82 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Revision Exercises (Additional Questions)
22 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - NCERT (Exemplar Problems Subjective Questions) (Very Short Answer Type Questions)
11 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
12 Videos
Similar Questions
A rod made of glass (μ=1.5) and of square cross-section is equal is bent into the shape shown in figure. A parallel beam of light falls perpendicurly on the plane flat surface . A . Referring to the diagram, d is the width of a side & R is radius of inner semicircle. find the maximum value of ratio dR so that all light entering the glass through surface A emerge from the glass through surface B.
_E01_133_Q01.png)
View SolutionThe Figure shows the equatorial circle of a glass sphere of radius R having centre at C. The eye of an observer is located in the plane of the circle at a distance R from the surface. A small insect is crawling along the equatorial circle.
(a) Calculate the length (L) of the are on the circle where the insect lies where its image is visible to the observer.
(b) Calculate the value of L when the eye is brought very close to the sphere. Refractive index of the glass is μ=1√2
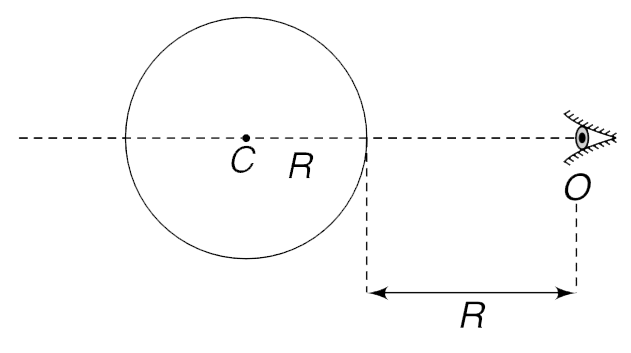
View Solution
Knowledge Check
A rod of glass (μ=1.5) and of square cross section is bent into the shape shown in the figure. A parallel beam of light falls on the plane flat surface A as shown in the figure. If d is the width of a side and R is the radius of circular arc then for what maximum value of dR light entering the glass slab through surface A emerges from the glass through B
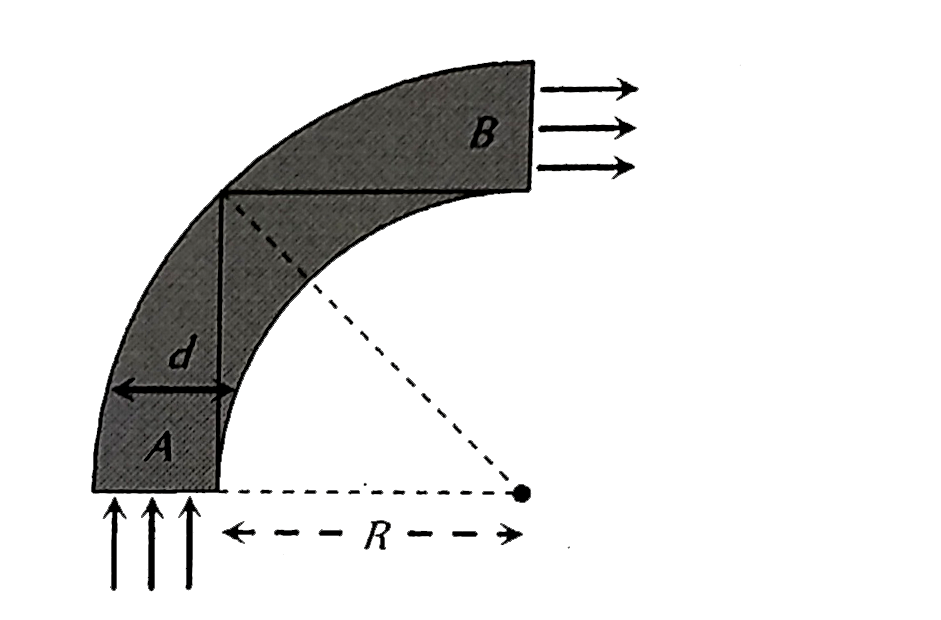 A1.5B0.5C1.3DNone of these
A1.5B0.5C1.3DNone of theseA sound wave of wavelength 32 cm enters the tube at S as shown in the figure. Then the smallest radius r so that a minimum of sound is heard at detector D is
 A7cmB14cmC21cmD28cm
A7cmB14cmC21cmD28cmA glass prism of refractive index 1.5 is placed in water of refractive index 1.33. The minimum value of the angle of the prism so that it will not be possible to have any emergent ray is
A150∘B125∘C165∘D180∘
A glass sphere of refractive index 1.5 forms the real image of object O at point I as shown in the figure when kept in air of refractive index 1. If the value of x is kR. Find k

View SolutionAn object is at a distance of d=2.5cm from the surface of a glass sphere with a radius R=10cm. Find the position of the final image produced by the sphere. The refractive index of glass is μ1.5.
View SolutionA glass prism in the shape of a quarter cylinder lies on a horizontal table. A uniform horizontal light beam falls on its vertical plane surface as shown in the figure. If the radius of the cylinder is R = 5cm and the refractive index of the glass is n = 1.5 where on the table beyond the cylinder will a path of light be found? (in cm) Light R
View SolutionLight is incident at an angle i on one planer end of a transparent cylinderical rod of refractive index μ. Find the least value of μ so that the light entering the rod does not emerge from the curved surface of the rod irrespective of the value of i.

View Solution(a) Draw the ray diagram showing refraction of ray of light through a glass prism. Derive the expression for the refractive index n of the material of prism in terms of the angle A ray angle of minimum deviation δm
(b) A ray of light PQ enters an isosceles right angles prism ABC of refractive index 1.5 as shown in figure .
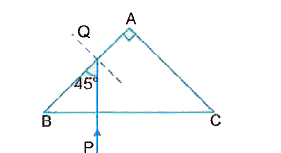
(i) Trace the path of the ray through the prism .
(ii) What will be the effect on the path of the ray if refractive index of the prism is 1.4 ?
View Solution