A heavy ball moving with speed v collides with a tiny ball. The collision is elastic, then immediately after the impact, the second ball will move with a speed approximately equal to
(a) v
(b) 2v
(c) v2
(d) v3
The correct Answer is:B
To solve the problem of a heavy ball colliding elastically with a tiny ball, we can use the principles of conservation of momentum and conservation of kinetic energy. Here's a step-by-step solution:
Step 1: Define the masses and initial velocities
Let:
- Mass of the heavy ball = M
- Mass of the tiny ball = m
- Initial velocity of the heavy ball = v
- Initial velocity of the tiny ball = 0 (since it is at rest)
Step 2: Apply conservation of momentum
The total momentum before the collision must equal the total momentum after the collision. Therefore, we can write:
M⋅v+m⋅0=M⋅v′+m⋅u
where v′ is the final velocity of the heavy ball and u is the final velocity of the tiny ball.
Step 3: Apply conservation of kinetic energy
Since the collision is elastic, the total kinetic energy before the collision must equal the total kinetic energy after the collision:
12Mv2+12m⋅02=12M(v′)2+12mu2
This simplifies to:
12Mv2=12M(v′)2+12mu2
Step 4: Solve the equations
From the momentum equation:
Mv=Mv′+mu(1)
From the kinetic energy equation:
Mv2=M(v′)2+mu2(2)
Step 5: Analyze the scenario
Given that the mass of the heavy ball M is much larger than the mass of the tiny ball m, we can make an approximation. After the collision, the heavy ball will continue moving with a velocity close to its initial velocity v, and the tiny ball will gain a significant amount of speed.
Step 6: Approximate the final speed of the tiny ball
In a perfectly elastic collision where one object is much heavier, the tiny ball will move away with a speed approximately equal to twice the speed of the heavy ball before the collision:
u≈2v
Conclusion
Thus, the speed of the tiny ball immediately after the impact will be approximately equal to 2v.
Final Answer
The second ball will move with a speed approximately equal to 2v.
---
Let:
- Mass of the heavy ball = M
- Mass of the tiny ball = m
- Initial velocity of the heavy ball = v
- Initial velocity of the tiny ball = 0 (since it is at rest)
The total momentum before the collision must equal the total momentum after the collision. Therefore, we can write:
M⋅v+m⋅0=M⋅v′+m⋅u
where v′ is the final velocity of the heavy ball and u is the final velocity of the tiny ball.
Since the collision is elastic, the total kinetic energy before the collision must equal the total kinetic energy after the collision:
12Mv2+12m⋅02=12M(v′)2+12mu2
This simplifies to:
12Mv2=12M(v′)2+12mu2
From the momentum equation:
Mv=Mv′+mu(1)
From the kinetic energy equation:
Mv2=M(v′)2+mu2(2)
Given that the mass of the heavy ball M is much larger than the mass of the tiny ball m, we can make an approximation. After the collision, the heavy ball will continue moving with a velocity close to its initial velocity v, and the tiny ball will gain a significant amount of speed.
In a perfectly elastic collision where one object is much heavier, the tiny ball will move away with a speed approximately equal to twice the speed of the heavy ball before the collision:
u≈2v
Thus, the speed of the tiny ball immediately after the impact will be approximately equal to 2v.
The second ball will move with a speed approximately equal to 2v.
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Subjective
32 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Subjective Questions
1 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Assertion And Reason
15 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
A massive ball moving with speed v collieds with a tiny ball which is intially at rest having a mass very much smaller than the mass of the first ball. The collision is elastic, then immediately after the impact, the second ball will move with a speed approximately equal to :-
View SolutionA ball is moving with speed 20ms−2 collides with a smooth surface as shown in figure. The magnitude of change in velocity of the ball will be

View Solution
Knowledge Check
A ball of mass m moving with a speed 2v0 collides head-on with an identical ball at rest. If e is the coefficient of restitution, then what will be the ratio of velocity of two balls after collision?
A1−e1+eBe−1e+1C1+e1−eDe+1e−1
A ball is moving with speed 20ms−2 collides with a smooth surface as shown in figure. The magnitude of change in velocity of the ball will be

View SolutionTwo billiard balls undergo a head-on collision. Ball 1 is twice as heavy as ball 2. Initially, ball 1 moves with a speed v towards ball 2 which is at rest. Immediately after the collision, ball 1 travels at a speed of v/3 in the same direction. What type of collision has occured?
View SolutionSTATEMENT - 1 : Two identical balls B and C lie on a horizontal smooth straight groove so that they are touching. A third identical ball A moves at a speed v along the groove. And collides with B as shown in figure. If the collisions are perfectly elastic, then after the collision, balls A and B will come to rest and ball C moves with velocity v to the right.
because

STATEMENT - 2 : In an elastic collision, linear momentum and kinetic energy are both conserved.
View SolutionA ball of mass m moving with velocity v, collide with the wall elastically as shown in the figure. After impact the change in angular momentum about P is :
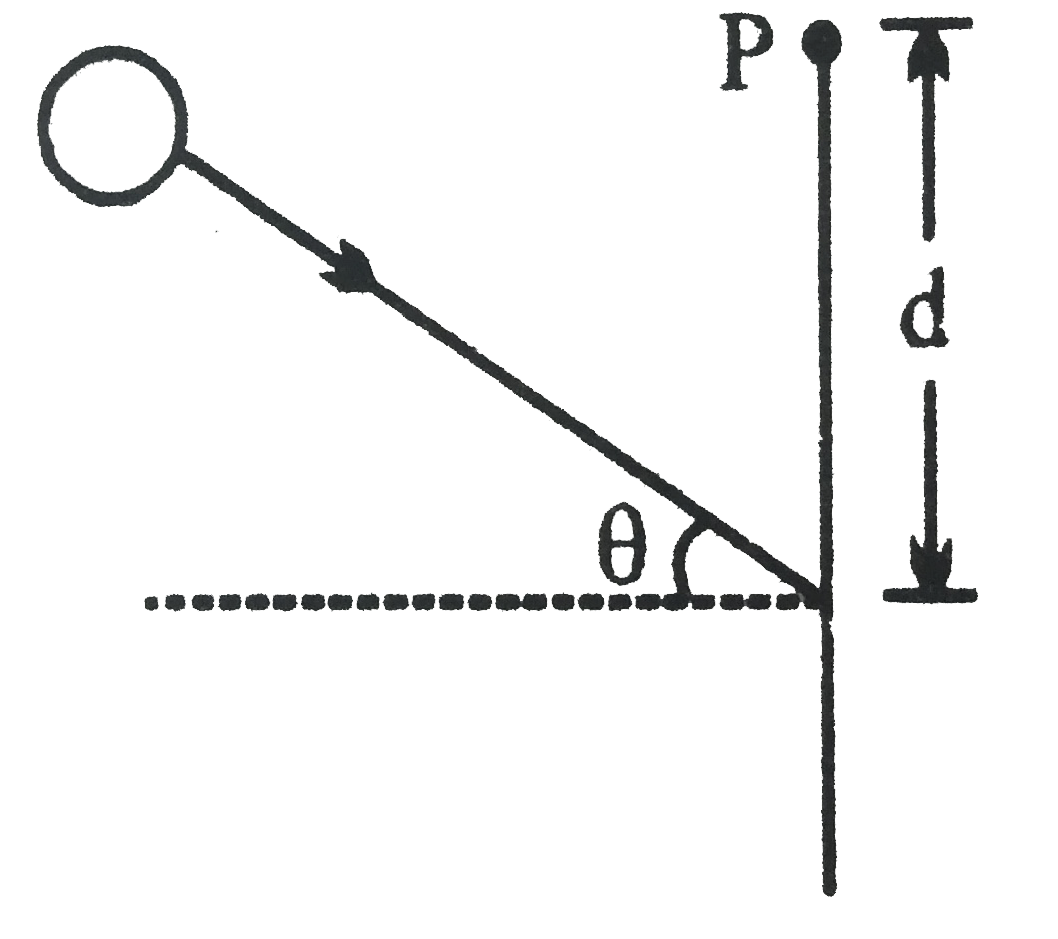 .
.
View SolutionA ball of mass 5 kg moving with speed 8 m/s collides head on with another stationary ball of mass 15 kg. If collision is perfectly inelastic, then loss in kinetic energ is
View SolutionA smooth ball 'A' moving with velocity 'V' collides with another smooth identical ball at rest. After collision both the balls move with same speed with angle between their velocities 60∘. No external force acts on the system of balls.

The speed of each ball after the collision is
View SolutionA ball moving on a horizontal frictionless plane hits an identical ball at rest with a velocity of 0.5m/s. If the collision is elastic, calculate the speed imparted to the target ball, if the speed of projectile after the collision is 30cm/s.
View Solution
