A heavy particle of mass m is in motion on a smooth surface of hemisphere of radius R and there is no friction. At the initial instant the particle is at the topmost point A and has an initial velocity v0 At what point will the particle leave the surface of the hemisphere ? Also determine the value of v0 for which the particle will leave the sphere at the initial instant.
The correct Answer is:A, B, C
Step by step video, text & image solution for A heavy particle of mass m is in motion on a smooth surface of hemisphere of radius R and there is no friction. At the initial instant the particle is at the topmost point A and has an initial velocity v_(0) At what point will the particle leave the surface of the hemisphere ? Also determine the value of v_(0) for which the particle will leave the sphere at the initial instant. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - unsolved
1 Videos
- WORK, ENERGY AND POWERBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - MCQ
158 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Unsolved Numerical
63 Videos
Similar Questions
A particle of mass m slides down from the vertex of semi- hemisphere, without any initial velocity. At what height from horizontal will the particle leave the sphere-
View SolutionA particle of mass m is released from the top of a smooth hemisphere of radius R with the horizontal speed μ. Calculate the angle with verticle where it loses contact with the hemisphere.
View Solution
Knowledge Check
A particle of mass m is going along surface of smooth hemisphere of radius R in verticle plane. At the moment shown its speed is v. Choose correct option(s).
 Amg−Ncosθ=m(gsin2θ−v2Rcosθ)BN−mgcosθ=mv2RCmg−Nsinθ=mv2RDNsinθ=m(gsinθcosθ−v2Rsinθ)
Amg−Ncosθ=m(gsin2θ−v2Rcosθ)BN−mgcosθ=mv2RCmg−Nsinθ=mv2RDNsinθ=m(gsinθcosθ−v2Rsinθ)A particle of mass m is being circulated on a vertical circle of radius r. If the speed of particle at the highest point be v, then
Amg=mv2rBmg>mv2rCmg≤mv2rDmg≥mv2rA particle is released from the top of the smooth hemisphere R as shown.
the normal contact between the particle and the hemisphere in position θ is
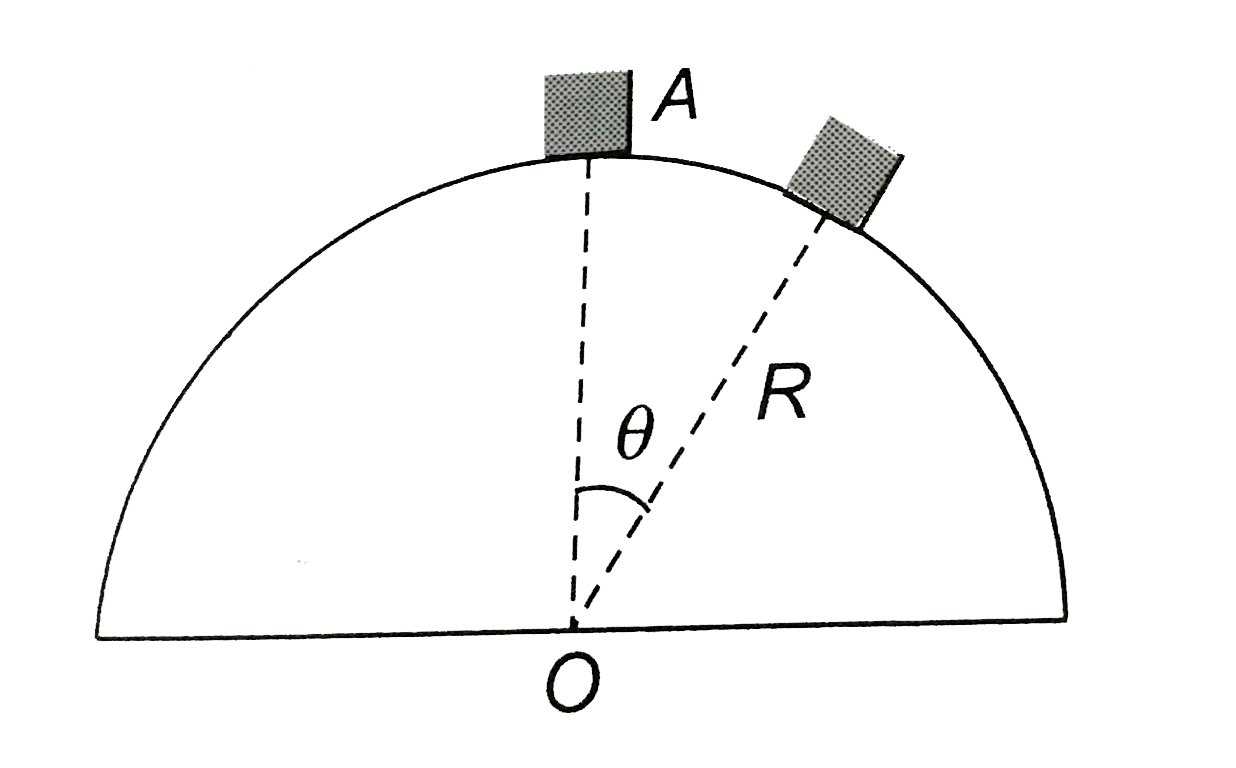 Amg(3−2cosθ)Bmg(3cosθ−2)Cmg(4cosθ−3)Dmg(4−3cosθ)
Amg(3−2cosθ)Bmg(3cosθ−2)Cmg(4cosθ−3)Dmg(4−3cosθ)
A particle slides down from the top outside smooth surface of a fixed sphere of radius a=10m . The initial horizontal velocity to be imparted to the particle at the top is 5Km/s ,if it leaves the surface at a point whose vertical height above the centre of sphere is 3a/4. Find the value of K
View SolutionA particle of mass m moves along the internal smooth surface of a vertical cylinder of radius R. Find the force with which the particle acts on the cylinder wall if at the initial moment of time its velocity equals v0 and forms an angle α with the horizontal.
View SolutionA particle of mass m oscillates inside the smooth surface a fixed pipe of radius R. The axis of the pipe is horizontal and the particle moves from B to A and back. At an instant the kinetic energy of the particle is K (say at position of the particle shown in figure ). Then choose the correct value of force applied by particle on the pipe at this instant.
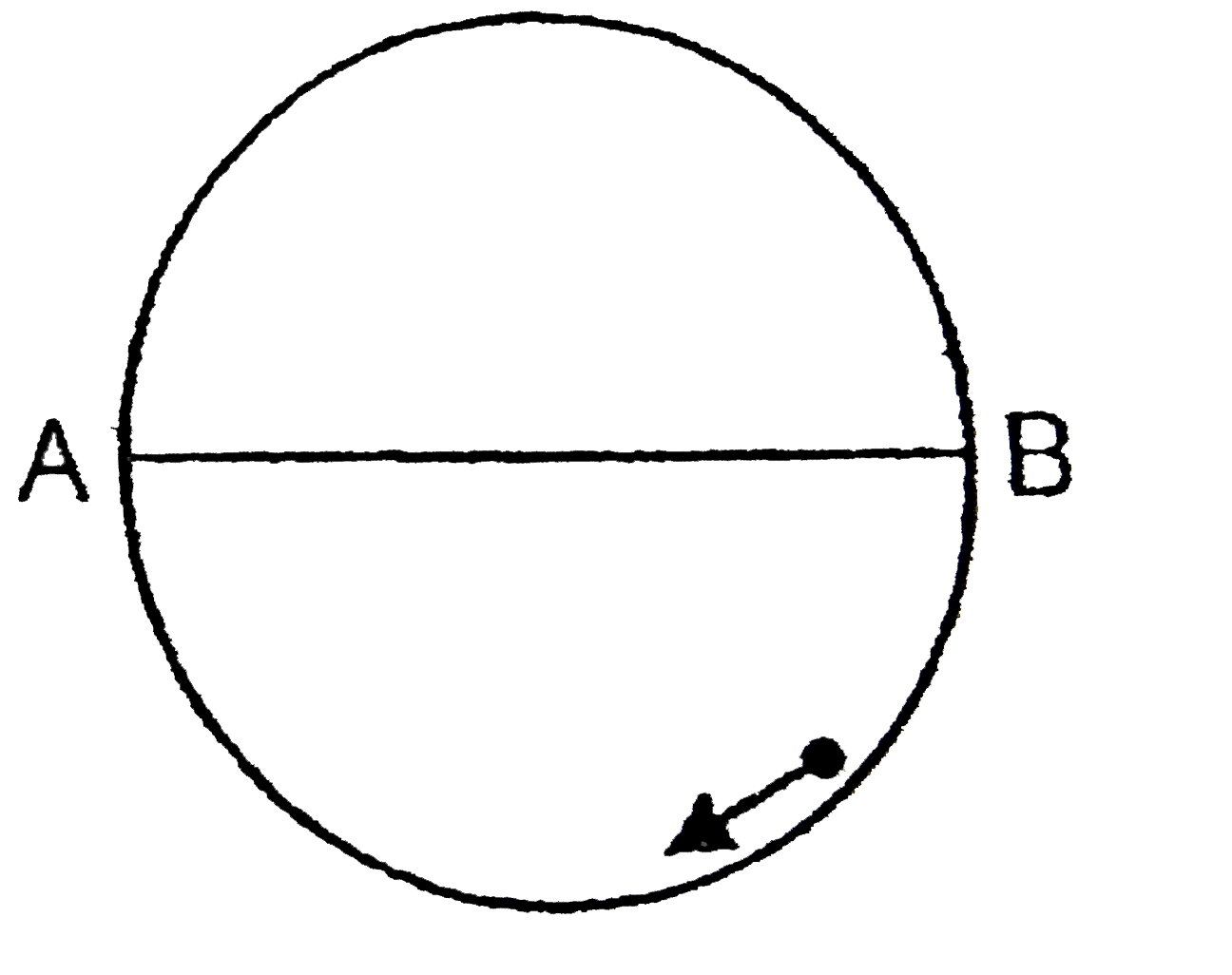
View SolutionA particle of mass m moves along the internal smooth surface of a vertical cylinder of the radius R. Find the force with which the particle acts on the cylinder wall if at the initial moment of time its velocity equals v0. And forms an angle α with the horizontal.
View SolutionA particle of mass m oscillates inside a smooth spherical shell of radius R and starts its motion from point B. At given instant the kinetic energy of the particle is K. Then the force applied by particle on the shell at this instant is :−
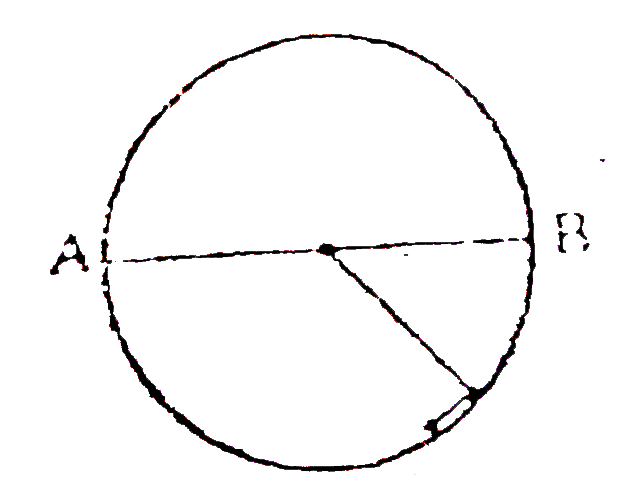
View Solution
