A hemisphere of mass 3m and radius R is free to slide with its base on a smooth horizontal table. A particle of mass m is placed on the top of the hemisphere. If particle is displaced with a negligible velocity, then find the anuglar velocity of the particle relative to the centre of the hemisphere at an angular displacement θ, when velocity of hemisphere is υ.
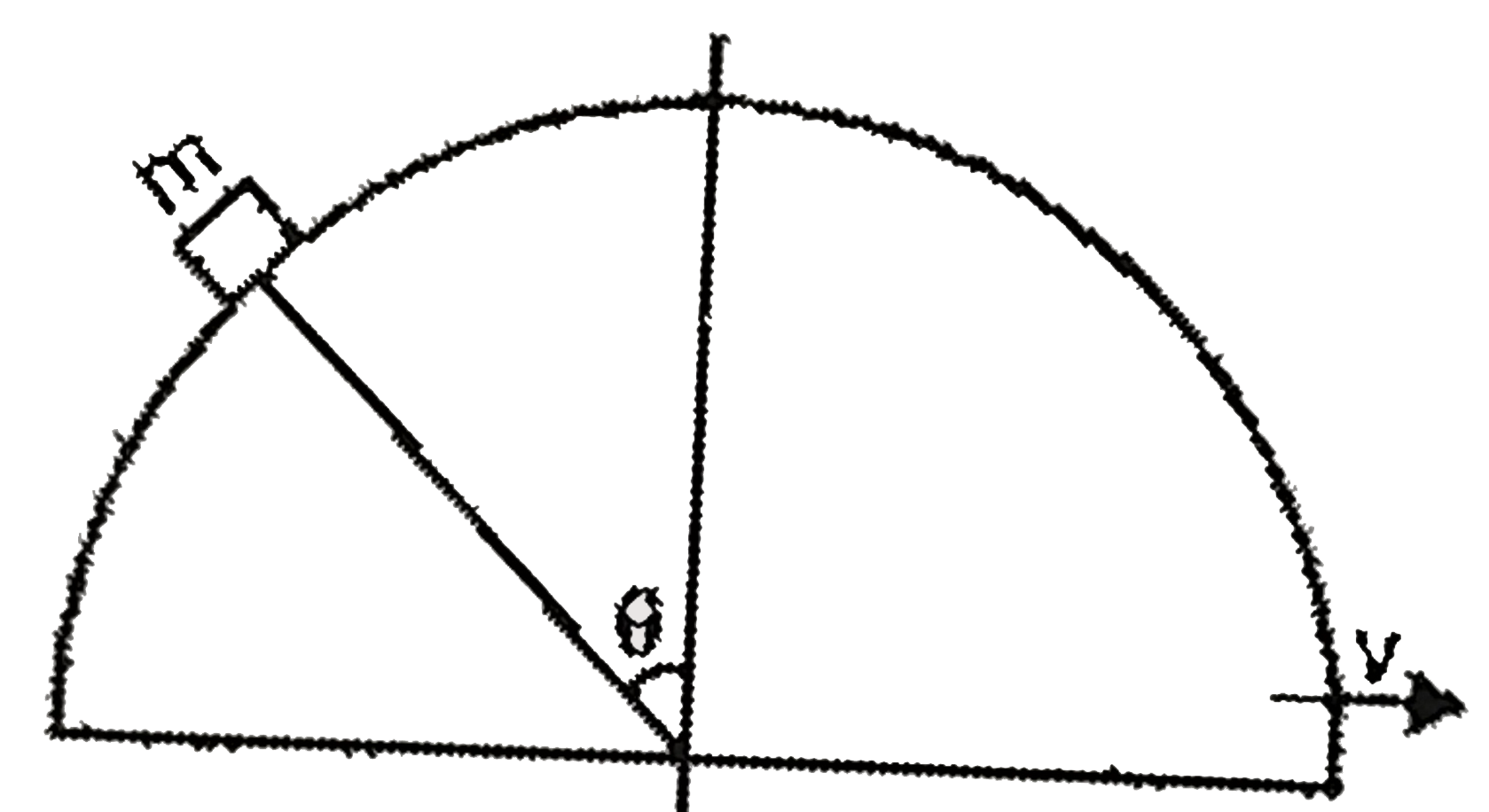
4υRcosθ
3υRcosθ
5υRcosθ
2υRcosθ
The correct Answer is:A
Topper's Solved these Questions
- BOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - L-221videos
IMPULSE AND MOMENTUM
- BOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - L-3,(P-1)5videos
IMPULSE AND MOMENTUM
- BOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - Example50videos
IMPULSE AND MOMENTUM
- BOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Matching type13videos
FORCE ANALYSIS
- BOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - MATCH THE COLUMN12videos
RIGID BODY MOTION
Similar Questions
A hemisphere of radius R and mass 4 m is free to slide with its base on a smooth horizontal table . A particle of mass m is placed on the top of the hemisphere . The angular velocity of the particle relative to centre of hemisphere at an angular displacement θ when velocity of hemisphere has become v is
View SolutionA hemisphere of radius R and mass 4 m is free to slide with its base on a smooth horizontal table . A particle of mass m is placed on the top of the hemisphere . The angular velocity of the particle relative to centre of hemisphere at an angular displacement θ when velocity of hemisphere has become v is
View Solution
Knowledge Check
- Question 1 - Select One
A small ball is placed at the top of a smooth hemispherical wedge of radius R. If the wedge is accelerated with an acceleration a, find the velocity of the ball relative to wedge as a function of θ.
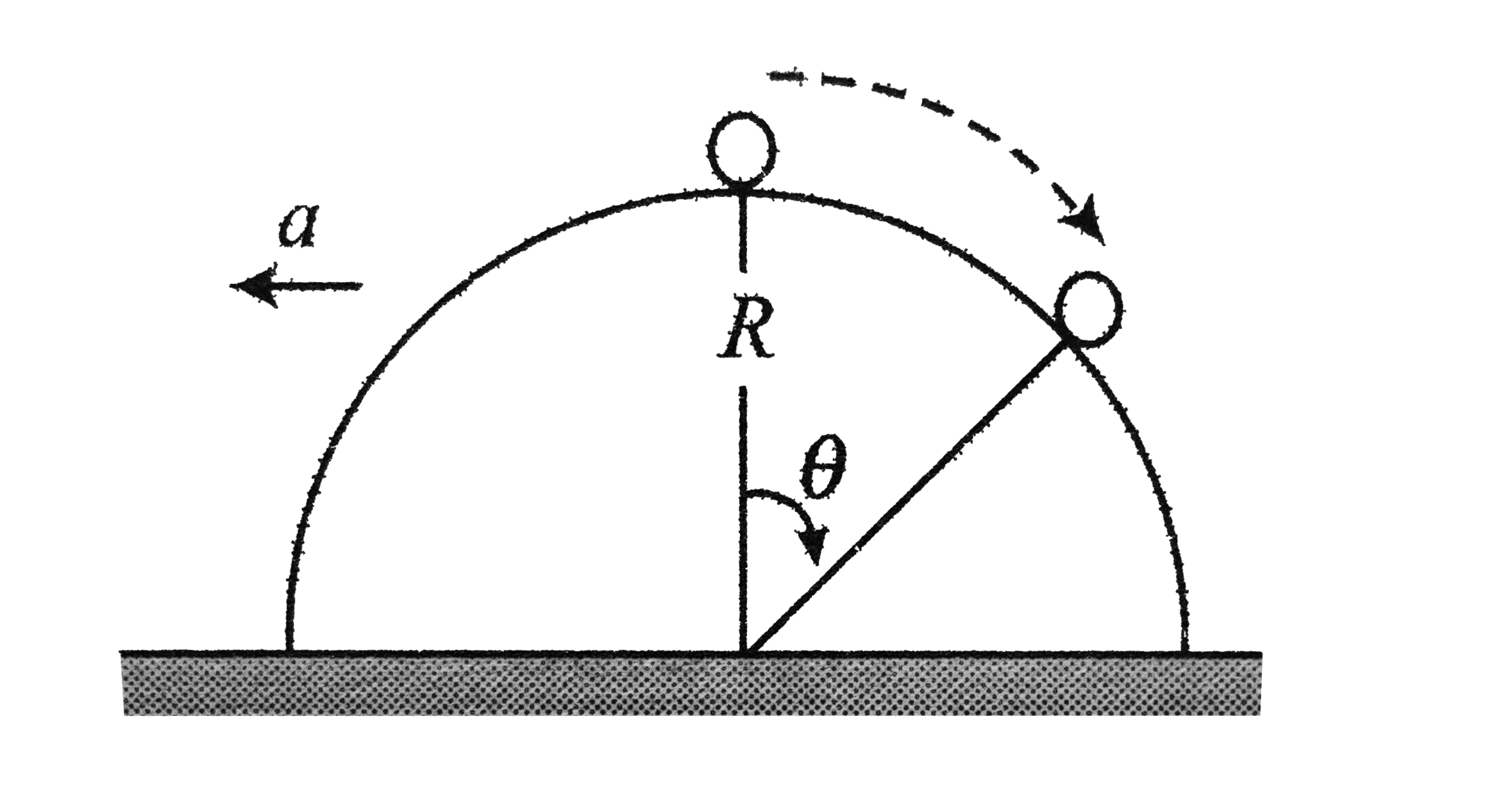 A√2R[g(1−sinθ)+aRcosθ]B√2R[g(1+cosθ)−aRsinθ]C√2R[g(1−cosθ)+aRsinθ]D√2R[g(1+sinθ)−aRcosθ]
A√2R[g(1−sinθ)+aRcosθ]B√2R[g(1+cosθ)−aRsinθ]C√2R[g(1−cosθ)+aRsinθ]D√2R[g(1+sinθ)−aRcosθ] - Question 2 - Select One
A partcle rests on the top of a hemisphere of radiu R. Find the smallest horizontal velocity that must be imparted to the particle if it is to leave the hemisphere without sliding down it-
A√gRB√2gRC√3gRD√5gR - Question 3 - Select One
A partcle rests on the top of a hemisphere of radius R. Find the smallest horizontal velocity that must be imparted to the particle if it is to leave the hemisphere without sliding down :
A√gRB√2gRC√3gRD√5gR
A hemisphere of radius R and of mass 4m is free to Slide with its base on a smooth horizontal table. A particle mass m is placed on the top of the hemisphere. Find the angular velocity of the particle relative to hemisphere at an angular displacement θ when velocity of hemisphere has become v.
 View Solution
View SolutionA small ball is placed at the top of a smooth hemispherical wedge of radius R. If the wedge is accelerated with an acceleration a, find the velocity of the ball relative to wedge as a function of θ.
 View Solution
View SolutionA particle of mass m is released from the top of a smooth hemisphere of radius R with the horizontal speed μ. Calculate the angle with verticle where it loses contact with the hemisphere.
View SolutionA disc of mass m and radius R lies flat on a smooth horizontal table. A particle of mass m, moving horizontally along the table, strikes the disc with velocity V while moving along a line at a distance R2 from the centre. Find the angular velocity acquired by the disc if the particle comes to rest after the impact.
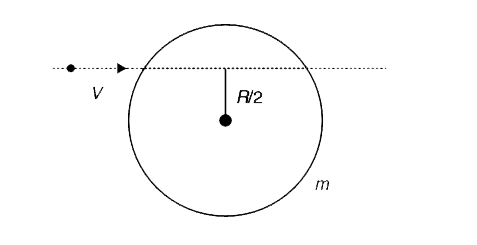 View Solution
View SolutionA smooth hemisphere of mass M is kept on a smooth surface. A block of mass m(=M/3) is kept on the top of the hemisphere as shown in the figure. The hemisphere is displaced slightly ang both the hemisphere and the block starts moving. At an angle θ with the vertical ( subtended by the block at the centre of the hemisphere ) , the relation between the velocity of the block ( V) and the velocity of the hemishere ( v0 ) is (V is the velocity of the block w.r.t. the hemisphere at that instant . )
 View Solution
View Solution

