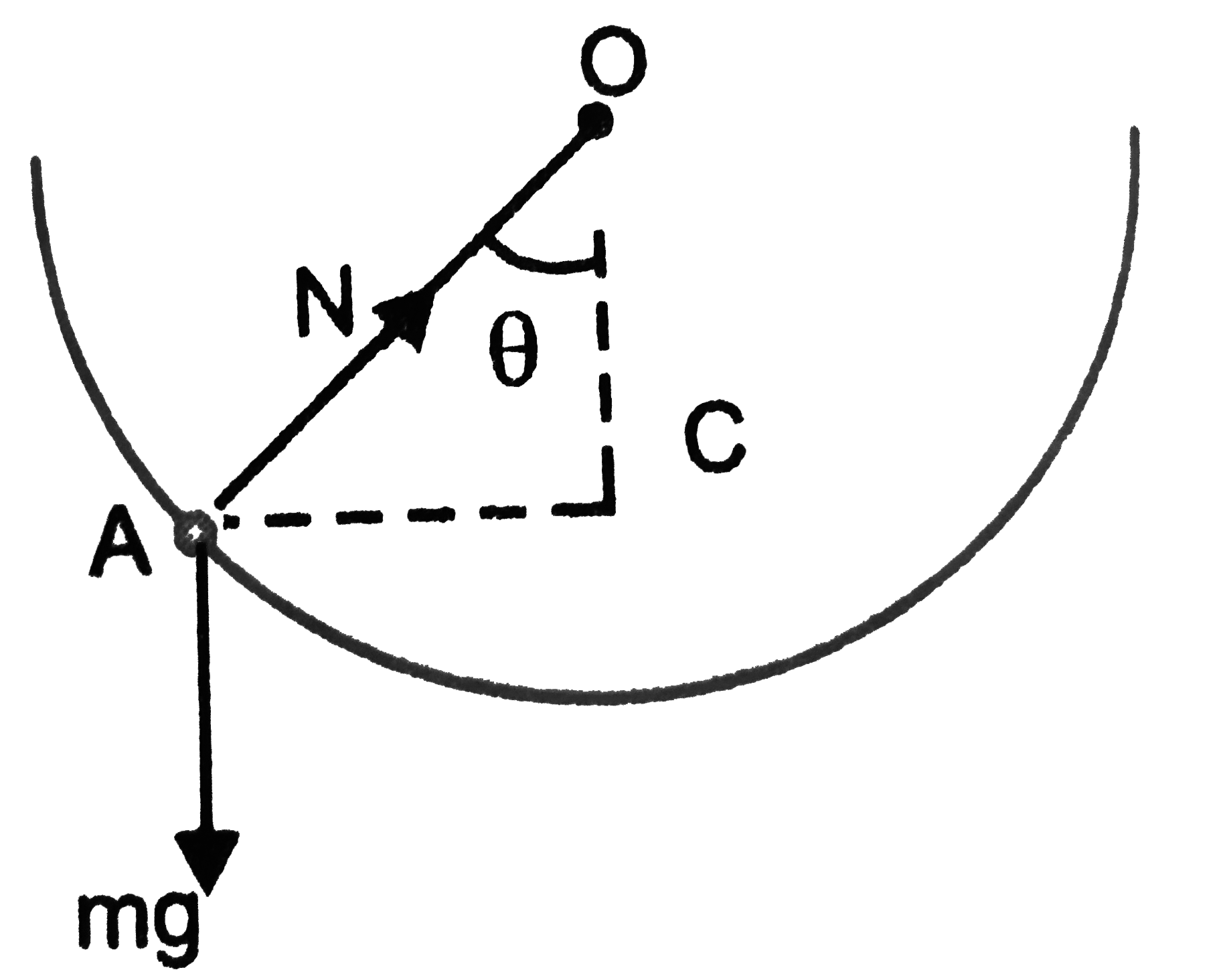
A hemispherical bowl of radius R is set rotating about its axis of symmetry which is kept vertical. A small block kept in the bowl rotates with the bowl without slipping on its surface. If the surfaces of the bowl is smooth, and the angle made by the radius through the block with the vertical is θ, find the angular speed at which the bowl is rotating.
Here OA=R,∠AOC=θ
Block moves in a horizontal circle with centre C and
radius r=AC=Rsinθ
∴ In equilibrium Ncosθ=mg
and Nsinθ=mω2(Rsinθ)
N=mω2R
From(i) mω2Rcosθ=mg
ω=√gRcosθ
 .
.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Value Based Questions with Answers
5 Videos
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Multiple Choice Questions
42 Videos
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Short Answer Questions
35 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 NCERT Comprehension
4 Videos
- MATHEMATICAL TOOLSBOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks
5 Videos
Similar Questions
A hemispherical bowl of radius R is set rotating about its axis of symmetry which is kept vertical. A small block kept in the bowl rotates with the bowl without slipping on its surface. If the surfaces of the bowl is smooth, and the angle made by the radius through the block with the vertical is θ, find the angular speed at which the bowl is rotating.
View SolutionA hemisphericla bowl of rdius R is rotated about its axis of symetry which is kept vertical.A small block is kept in the bowl at a position where the radius makes an angle θ with the vertical. The block rottes with the bowl without any sliping. The friction coefficient between the block and teh bowl surface is μ. Find the range of the angular speed for which the block will not slip.
View Solution
Knowledge Check
A spherical marble of radius r is made to oscillate in a bowl of radius R. What is its period of oscillation ?
AT=2π√RgBT=2π√R−rgCT=12π√gR−rDT=2π√gRA hollow cylinder of radius R rotates about its axis which is vertical. A block remains in contact with the inner wall if the frequency of rotation is f hertz, but falls at lower frequaencies. The coefficient of friction between the block and the cylinder is
Ag2π2f2RBg4π2f2RCgπ2RD2gπ2f2R
A hemispherical bowl of radius R=0.1m is rotating about its own axis (which is verticle) with an angular velocity ω. A particle of mass 10−2kg on the smooth inner surface of the bowl is also rotating with the same ω. The particle is at a height h from the bottom of the bowl (a) obtain the relation betweemn h and ω. what is the minimum value of ω needed, in order to have a non-zero value of h? (b) it is desired to measure g using this set up, by measuring h accurately. assuming that R and Ω are known precisely and least count in the measurement of h is 10−4m, what is the minimum possible error Δg in the measured value of g? (g=10m/s2)
View SolutionA hemispherical bowl of radius R is rotating about its own axis (which is vertical) with an angular velocity ω . A particle on the frictionless inner surface of the bowl is also rotating with the same ω . The particle is a height h from the bottom of the bowl.
(i) Obtain the relation between h and ω _________
(ii) Find minimum value of ω needed, in order to have a non-zero value of h _____________ .
View SolutionA block is kept inside a hemispherical bowl rotating with angular velocity ω. Inner surface of bowl is rough, coefficient of friction is μ. The block is kept at a position where radius makes an angle θ with the vertical. What is the range of the angular speed for which the block will stay at the given position?
View SolutionIf the coefficient of friction between an insect and bowl is μ and the radius of the bowl is r, find the maximum height to which the insect can crawl in the bowl.
View SolutionA ball of radius r is made to oscillate in a bowl of radius R, find its time period of oscillation.
View SolutionA disc of radius 4m is rotating about its fixed centre with a constant angular velocity 2rads (in the horizontal plane).A block is also rotating with the disc without slipping. If co-efficient of friction between the block and the disc is 0.4 ,then the maximum distance at which the block can rotate without
View Solution
