A hemispherical shell is uniformly charge positively. The electric field at point on a diameter away from the center is directed
perpendicular to the diameter
parallel to the diameter
at an angle tilted towards the diameter
at an angle tilted away from the diameter.
The correct Answer is:A
To find the direction of the electric field at a point on the diameter of a uniformly positively charged hemispherical shell, we can follow these steps:
1. Understand the Configuration:
- We have a hemispherical shell that is uniformly charged positively.
- We need to find the electric field at a point on the diameter of the shell, away from the center.
2. Identify the Point of Interest:
- Let's denote the center of the hemispherical shell as point O and the point on the diameter where we want to find the electric field as point A.
3. Consider the Symmetry:
- Due to the symmetry of the hemispherical shell, we can consider an elemental ring of charge on the surface of the shell.
- Each elemental charge on this ring will contribute to the electric field at point A.
4. Electric Field Contribution from the Ring:
- The electric field due to a ring of charge at a point along its axis (which is also the diameter in this case) is directed away from the ring if the charge is positive.
- The electric field E at a distance x from the center of the ring can be expressed as:
E=k⋅dQ⋅x(x2+R2)3/2
where dQ is the charge on the ring, R is the radius of the ring, and k is Coulomb’s constant.
5. Components of the Electric Field:
- Each elemental charge dQ on the ring produces an electric field component directed away from the ring.
- The components of the electric field that are parallel to the diameter will cancel out due to symmetry (as there are equal charges on either side of the diameter).
- The components of the electric field that are perpendicular to the diameter will add up.
6. Resultant Electric Field Direction:
- Since the parallel components cancel out, the net electric field at point A will be directed perpendicular to the diameter of the hemispherical shell.
- Given that the shell is positively charged, the direction of the electric field will be away from the shell.
7. Conclusion:
- Therefore, the electric field at point A on the diameter away from the center is directed perpendicular to the diameter of the shell.
Final Answer:
The electric field at the point on the diameter away from the center is directed perpendicular to the diameter.
---
- We have a hemispherical shell that is uniformly charged positively.
- We need to find the electric field at a point on the diameter of the shell, away from the center.
- Let's denote the center of the hemispherical shell as point O and the point on the diameter where we want to find the electric field as point A.
- Due to the symmetry of the hemispherical shell, we can consider an elemental ring of charge on the surface of the shell.
- Each elemental charge on this ring will contribute to the electric field at point A.
- The electric field due to a ring of charge at a point along its axis (which is also the diameter in this case) is directed away from the ring if the charge is positive.
- The electric field E at a distance x from the center of the ring can be expressed as:
E=k⋅dQ⋅x(x2+R2)3/2
where dQ is the charge on the ring, R is the radius of the ring, and k is Coulomb’s constant.
- Each elemental charge dQ on the ring produces an electric field component directed away from the ring.
- The components of the electric field that are parallel to the diameter will cancel out due to symmetry (as there are equal charges on either side of the diameter).
- The components of the electric field that are perpendicular to the diameter will add up.
- Since the parallel components cancel out, the net electric field at point A will be directed perpendicular to the diameter of the hemispherical shell.
- Given that the shell is positively charged, the direction of the electric field will be away from the shell.
- Therefore, the electric field at point A on the diameter away from the center is directed perpendicular to the diameter of the shell.
The electric field at the point on the diameter away from the center is directed perpendicular to the diameter.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDEXERCISE - MCQ s (More than One Options)
6 Videos
- ELECTRIC CHARGES AND FIELDBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDEXERCISE - Very short Type Question
6 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - LONG ANSWER TYPE QUESTION
5 Videos
- ELECTROMAGNETIC INDUCTION BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION EXERCISE - Long
11 Videos
Similar Questions
Knowledge Check
A hemispherical shell is uniformly charge positively .the electric field at point on a diameter away from the centre is directed
Aperpendicular to the diameterBparallel to the diameterCat an angle tilted towards the diameterDat an angle tilted away from the diameter
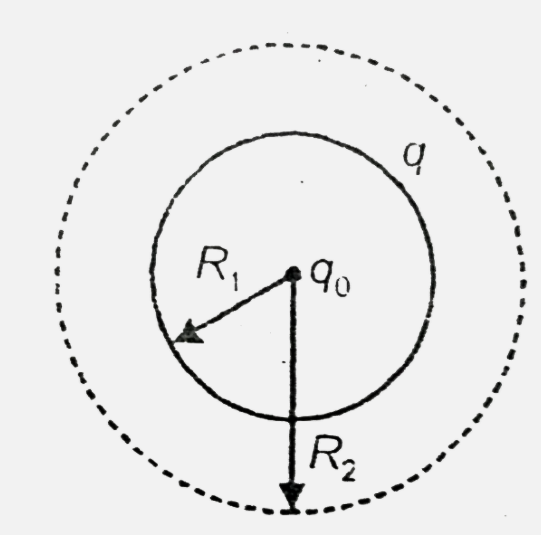
A sperical shell is uniformly charged by a charge q. A point charge q0 is at its centre , then
View SolutionFigure shows a uniformly charges hemispherical shell. The direction of electric field at point p that is off centre (but in the plane of the largest circle of the hemisphere), will be along

View SolutionFigure shows a uniformly charged hemisphere of radius R. It has a volume charge density ρ. If the electric field at a point 2R, above the its center is E, then what is the electric field at the point 2R below its center?

View SolutionA ring of radius a contains a charge q distributed. uniformly ober its length. Find the electric field at a point. on the axis of the ring at a distance x from the centre.
View SolutionConsider the previous problem , let the outer shell have the charge −4q. As in the above problem , the inner shell has the charge +2q. Calculate the electric field in terms of q and the distance r from the common center of the two shells for
r<a
View SolutionConsider the previous problem , let the outer shell have the charge −4q. As in the above problem , the inner shell has the charge +2q. Calculate the electric field in terms of q and the distance r from the common center of the two shells for
b<r<c
View SolutionConsider the previous problem , let the outer shell have the charge −4q. As in the above problem , the inner shell has the charge +2q. Calculate the electric field in terms of q and the distance r from the common center of the two shells for
a<r<b
View Solution
