A horizontal frictionless rod is threaded through a bead of mass . The length of the cart is and the radius of the bead, , is very small in comparison with . Initially at () the bead is at the right edge of the cart. The can is struck and as a result, it moves with velocity towards right. When the bead collides with the cart's walls, the collisions are always completely elastic.
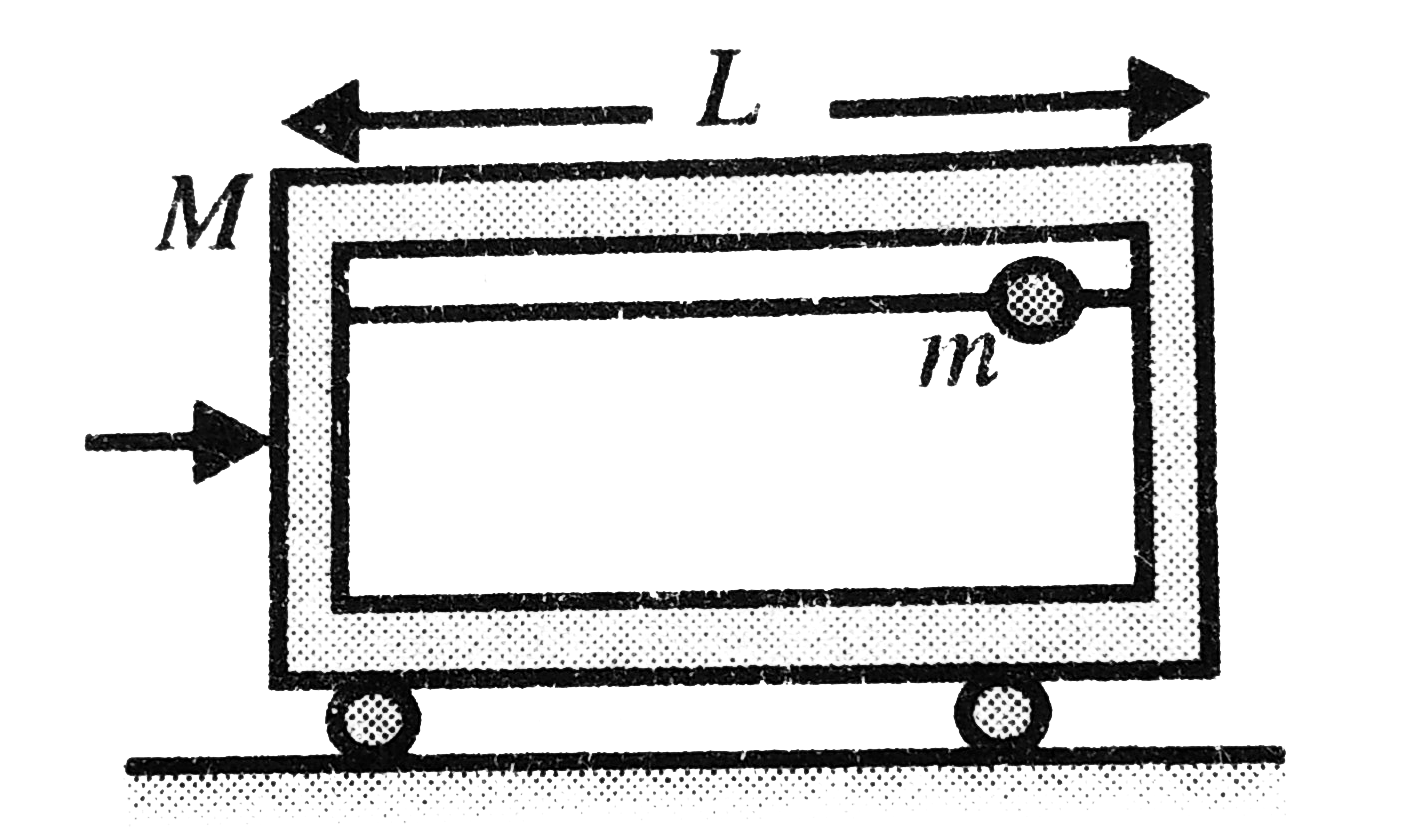
What is the velocity of the cart just after the first collision?
The correct Answer is:C

…………i
………..ii
Solve to get
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Integer
16 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Fill In The Blanks
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A horizontal frictionless rod is threaded through a bead of mass m. The length of the cart is L and the radius of the bead, r, is very small in comparison with L(r<<L). Initially at (t=0) the bead is at the right edge of the cart. The can is struck and as a result, it moves with velocity v0 towards right. When the bead collides with the cart's walls, the collisions are always completely elastic.
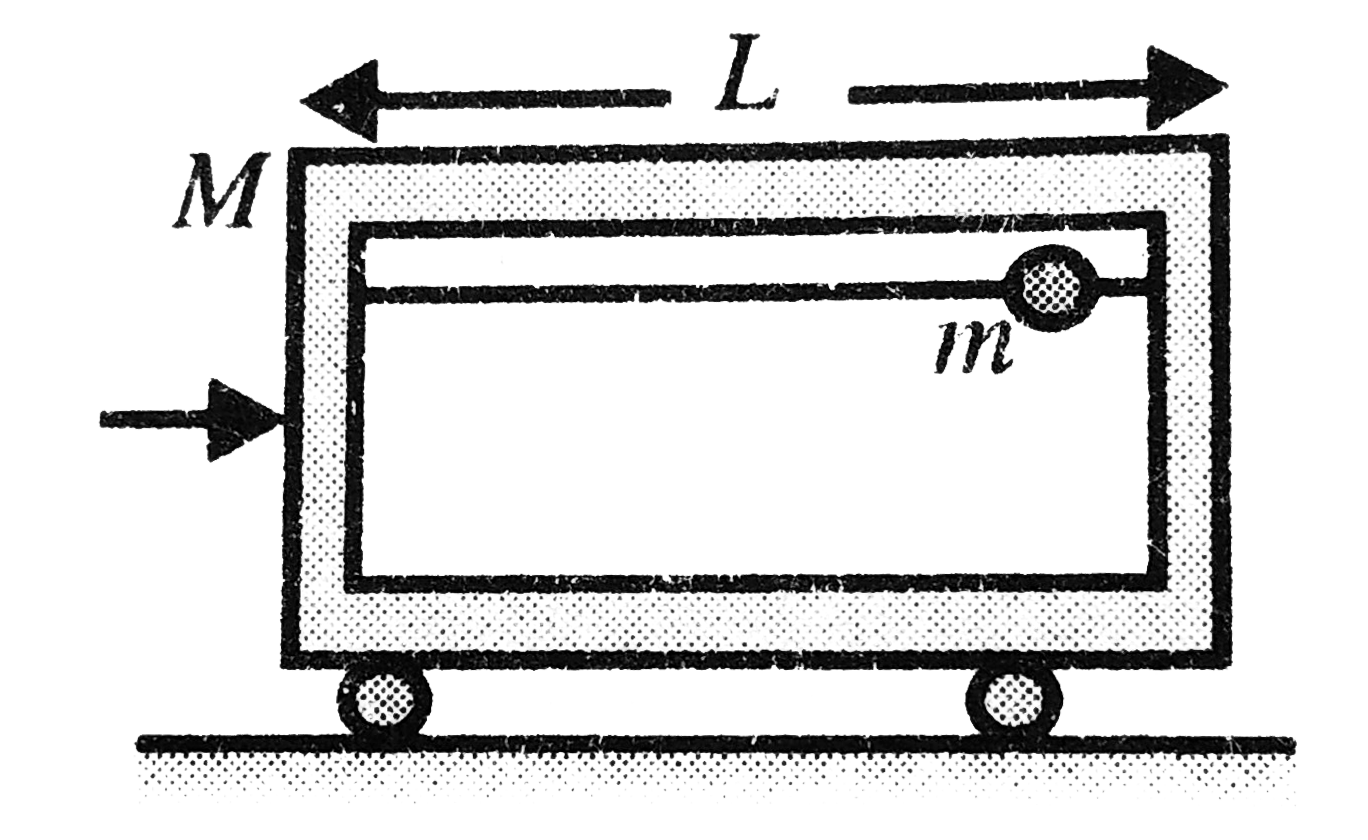
Velocity of bead just after the first collision is
View SolutionA horizontal frictionless rod is threaded through a bead of mass m. The length of the cart is L and the radius of the bead, r, is very small in comparison with L(r<<L). Initially at (t=0) the bead is at the right edge of the cart. The can is struck and as a result, it moves with velocity v0 towards right. When the bead collides with the cart's walls, the collisions are always completely elastic.
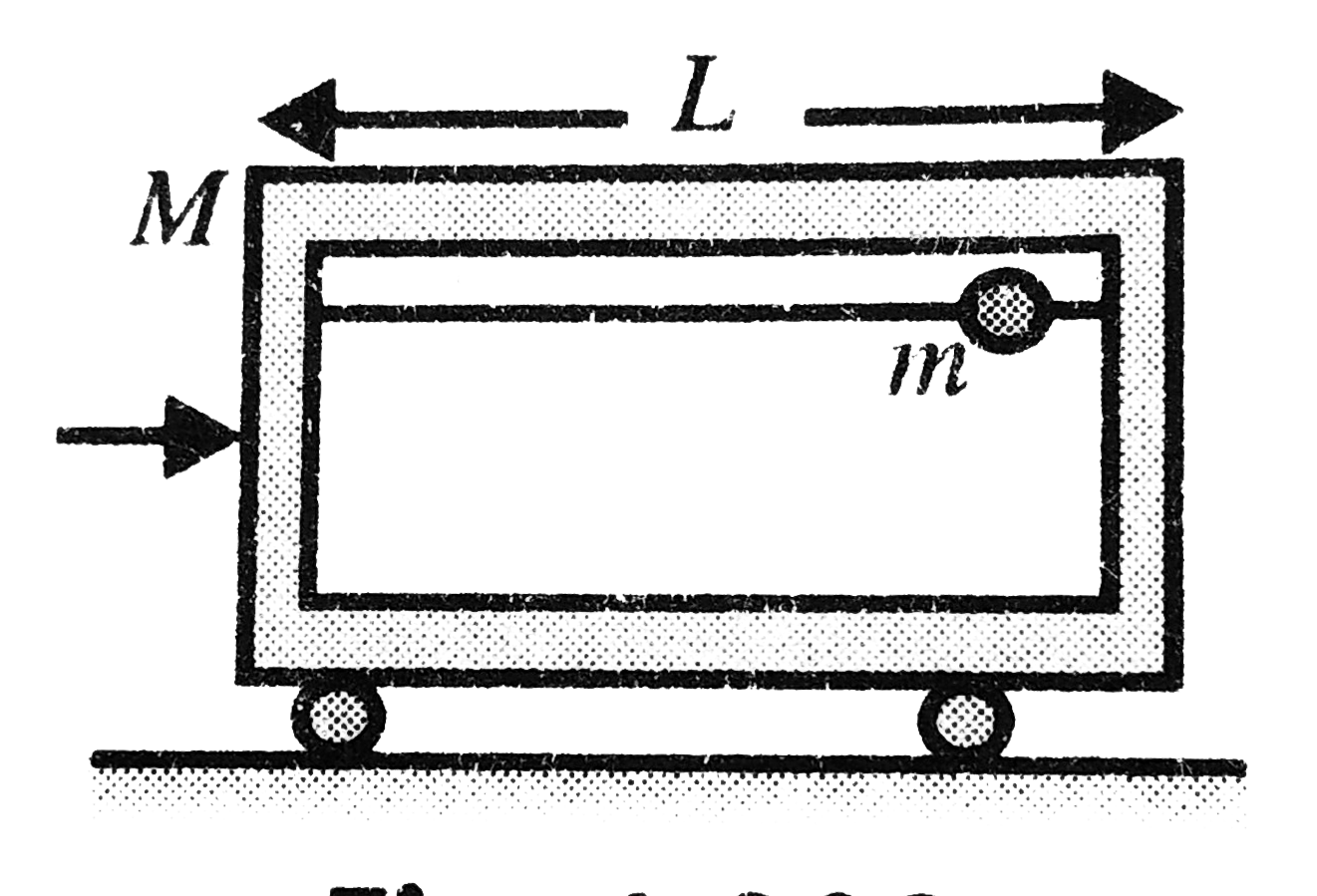
The first collision takes place at time ti and the second collision takes place at time t2. Find t2−t1
View SolutionA ball of mass in m=1kg is hung vertically by a thread of length l=1.50m. Upper end of the thread is attached to the ceiling of a trolley of mass M=4kg. Initially, the trolley is stationary and it is free to move along horizontal rails without friction. A shell of mass m=1 kg, moving horizontally with velocity v0=6m/s collides with the ball and gets stuck with it. As a result, the thread starts to deflect towards right.
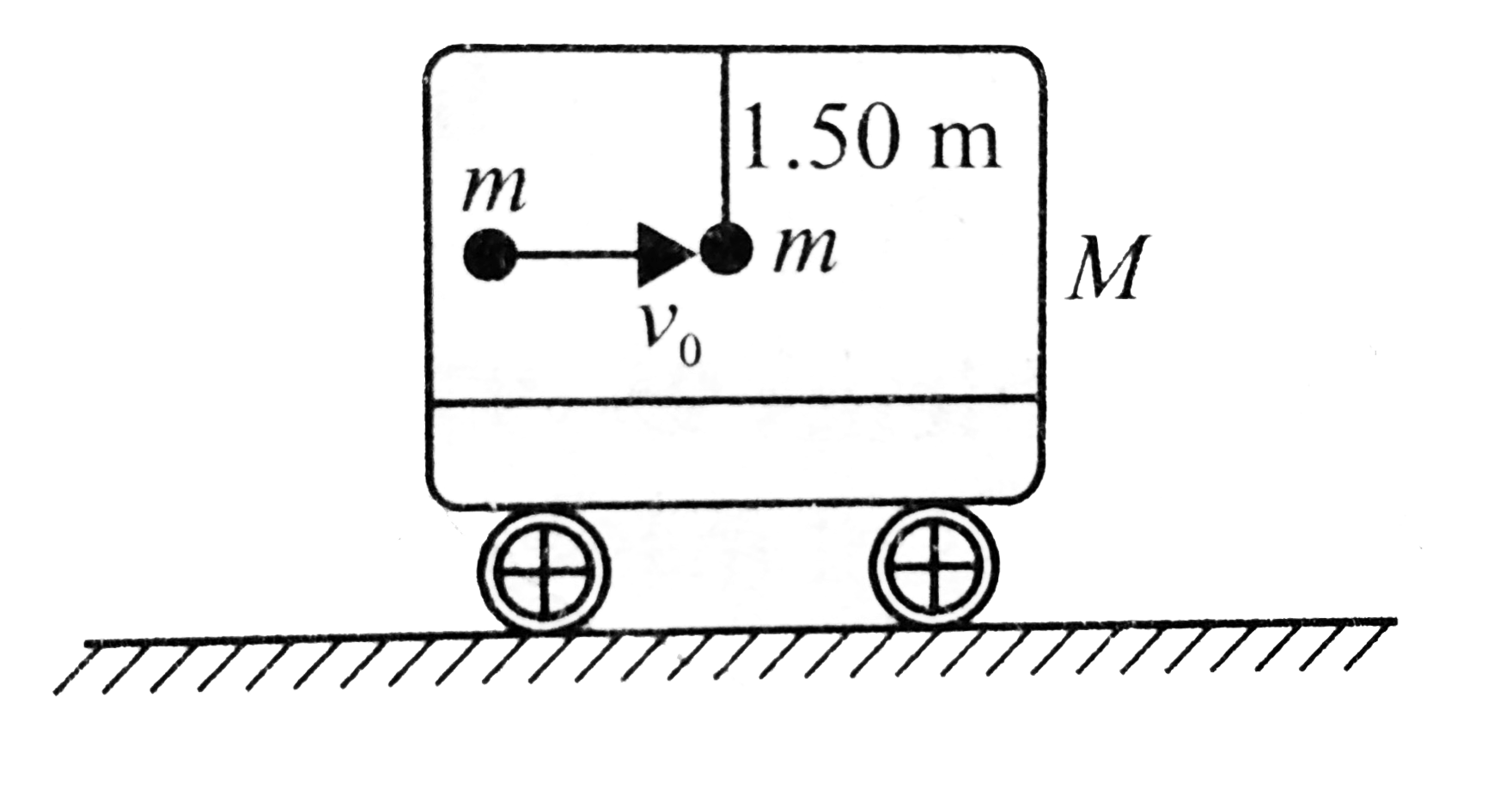
The velocity of the combined body just after collision is
View SolutionThe borax bead test can be used to detect the presence of
View SolutionA conducting rod AB of length l is projected on a frictionless frame PSRQ with velocity v0 at any instant. The velocity of the rod after time t is
View SolutionThe borax bead is due to formation of
View SolutionStructures called beads on string are
View SolutionA bead of mass m is fitted on a rod and can move on it without friction. Initially the bead is at the middle of the rod moves transitionally in the vertical plane with an accleration a0 in direction forming angle α with the rod as shown. The acceleration of bead with respect to rod is:
z
View SolutionA bead of mass m and diameter d is sliding back and forth with velocity v on a wire held between two right walls of length L. Assume that th ecollisions with the wall are perfectly elastic and ther is no friction. The average force that the bouncing bead exerts on the one of the walls is :_
View SolutionColour of the bead in borax bead test mainly due to the formation of
View Solution
