A horizontal frictionless rod is threaded through a bead of mass m. The length of the cart is L and the radius of the bead, r, is very small in comparison with L(r<<L). Initially at (t=0) the bead is at the right edge of the cart. The can is struck and as a result, it moves with velocity v0 towards right. When the bead collides with the cart's walls, the collisions are always completely elastic.
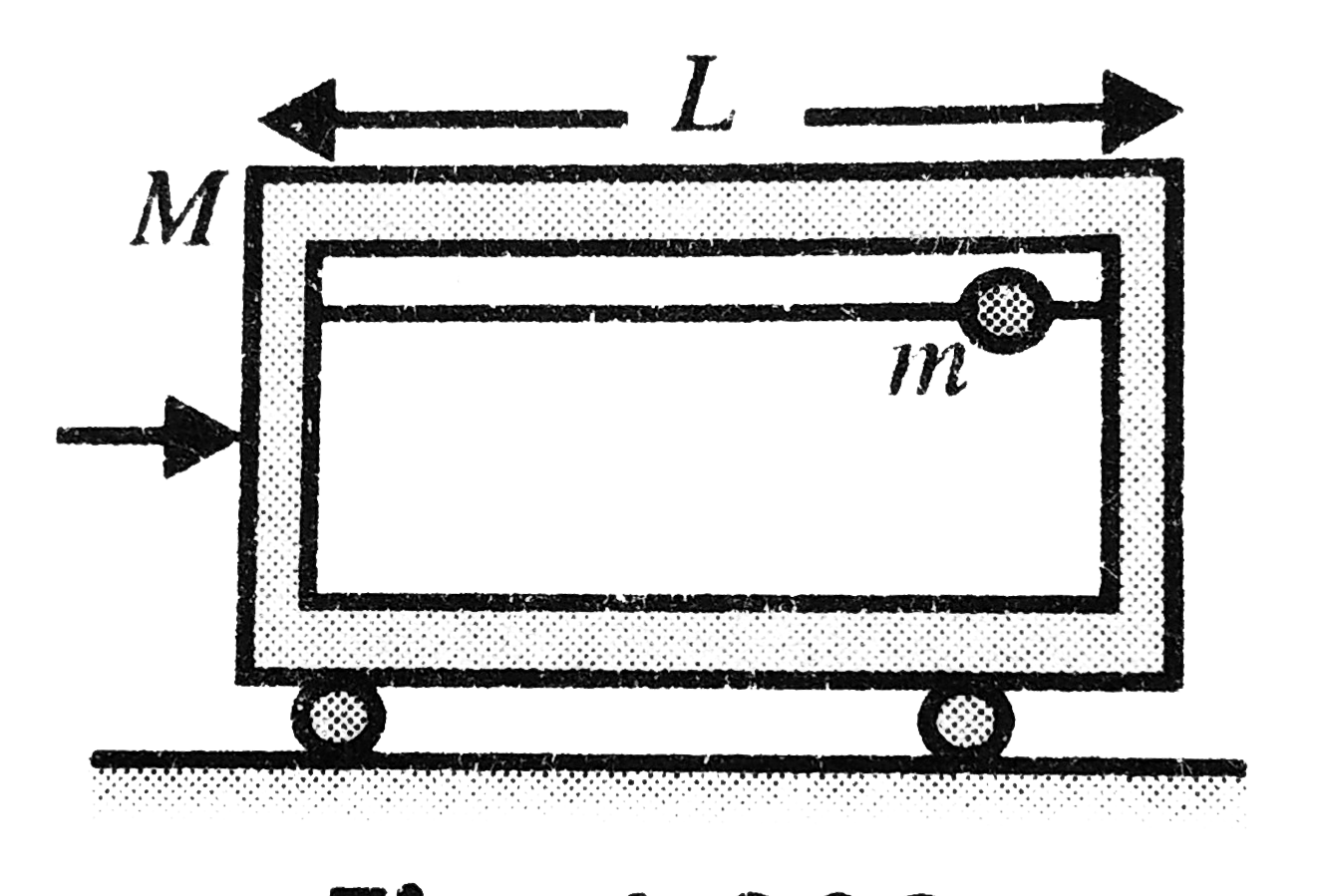
The first collision takes place at time ti and the second collision takes place at time t2. Find t2−t1
2Lv0
Lv0
L2v0
L3v0
The correct Answer is:B

Mv0=Mv1+mv2…………i
v2−v1v0=………..ii
Solve to get v1=M−mM+mv0
v2=2Mm+Mv0
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Integer16videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Fill In The Blanks2videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning2videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
Similar Questions
A horizontal frictionless rod is threaded through a bead of mass m. The length of the cart is L and the radius of the bead, r, is very small in comparison with L(r<<L). Initially at (t=0) the bead is at the right edge of the cart. The can is struck and as a result, it moves with velocity v0 towards right. When the bead collides with the cart's walls, the collisions are always completely elastic.
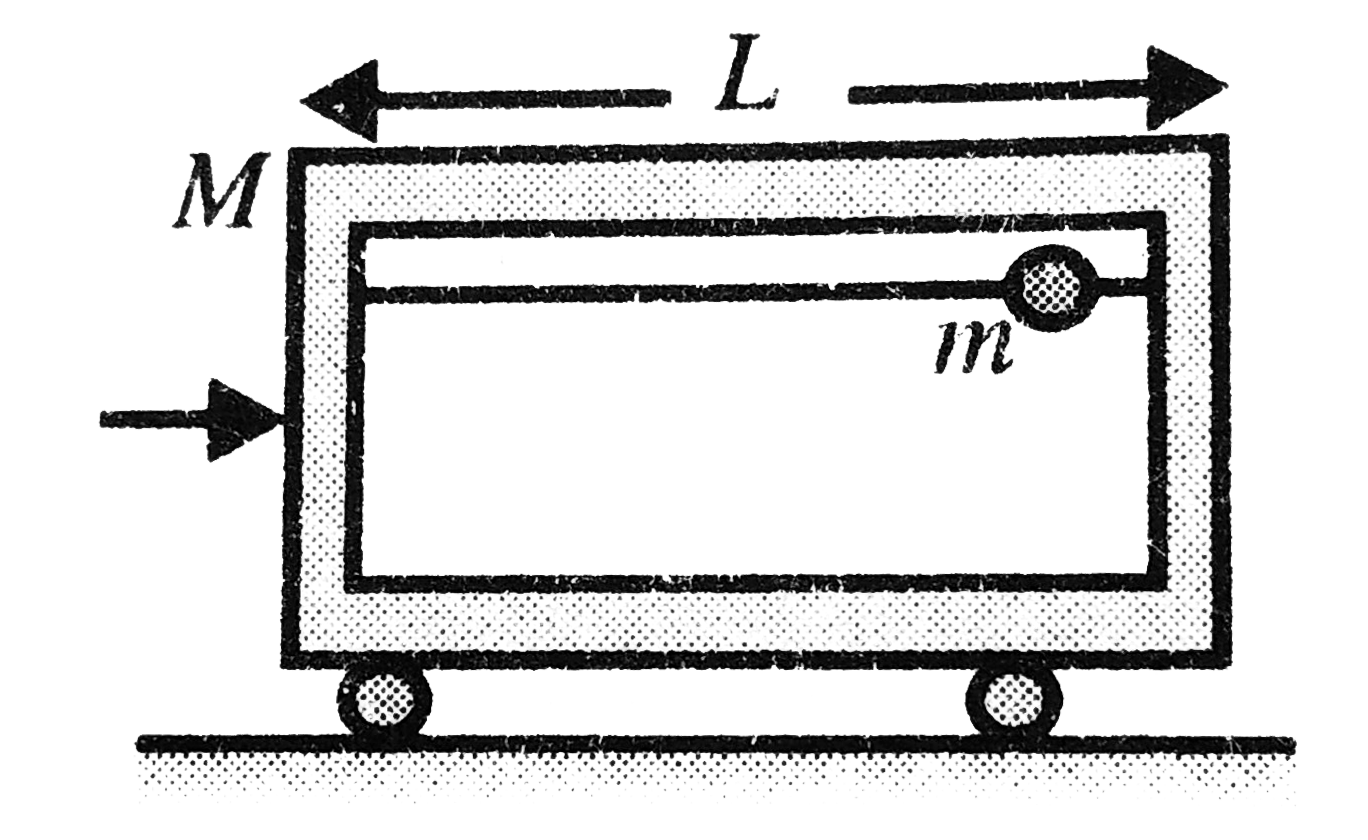
Velocity of bead just after the first collision isView SolutionA horizontal frictionless rod is threaded through a bead of mass m. The length of the cart is L and the radius of the bead, r, is very small in comparison with L(r<<L). Initially at (t=0) the bead is at the right edge of the cart. The can is struck and as a result, it moves with velocity v0 towards right. When the bead collides with the cart's walls, the collisions are always completely elastic.
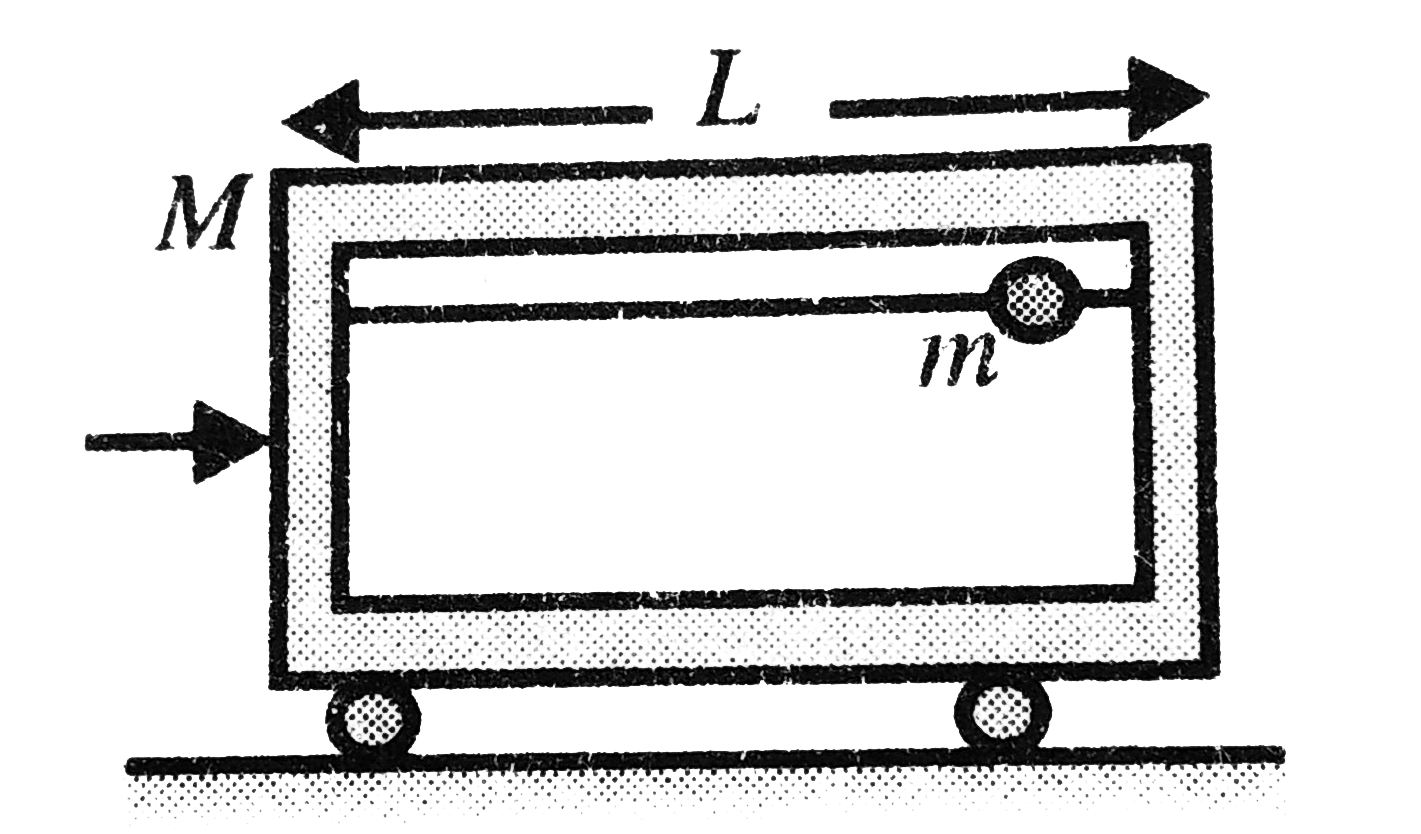
What is the velocity of the cart just after the first collision?View SolutionA bead of mass m and diameter d is sliding back and forth with velocity v on a wire held between two right walls of length L. Assume that th ecollisions with the wall are perfectly elastic and ther is no friction. The average force that the bouncing bead exerts on the one of the walls is :_
View SolutionA conducting rod AB of length l is projected on a frictionless frame PSRQ with velocity v0 at any instant. The velocity of the rod after time t is
View SolutionThe borax bead test can be used to detect the presence of
View SolutionStructures called beads on string are
View SolutionA bead of mass m is fitted on a rod and can move on it without friction. Initially the bead is at the middle of the rod moves transitionally in the vertical plane with an accleration a0 in direction forming angle α with the rod as shown. The acceleration of bead with respect to rod is:
zView SolutionColour of the bead in borax bead test mainly due to the formation of
View SolutionWhich of the following catio can not give bead test?
View SolutionBorax bead test is given by:
View Solution

