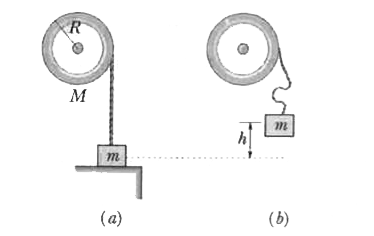
A horizontal, homogeneous cylinder of mass M and radius R is pivoted about its axis of symmetry. A string is wrapped several times around the cylinder and tied to a body of mass m resting on a support positioned so that the string has no slack. The body of mass m is then lifted vertically to a distance h, and then released.
(a) Evaluate the angular velocity of the cylinder, the speed of the falling body of mass m, and the kinetic energy of the system, just before the string becomes taut.
(b) Evaluate the corresponding quantities, , for the instant just after the string becomes taut.
(a) Since string is slack we can expect that the block will fall freely for distance l. Till this time tension in string will be zero.
Calculation: Just before the string becomes taut, the cylinder is still at rest. Since the tension remained zero nothing has caused the cylinder to begin turning. That is, . Since the string has exerted no force on the body of mass m, it has fallen freely with acceleration g thus . Same result can be derived by writing
work-kinetic energy theorem for the system. The kinetic energy of the system is given by
where is the inertia of the cylinder.
Putting , we get
(b) (1) The end attached to the block will be moving and it will pull the part of string touching the cylinder as the string becomes taut. (2) Thus, when string becomes tight an impulse/jerk will develop in the string. This jerk will start the motion of cylinder. There will be also an impulse due to axis of the cylinder. Here we can take cylinder, string and clock as our system. We will take axle of cylinder as the axis for writing angular momentum.
Calculations: The impulse due to jerk in string will produce internal angular impulse, and the impulse due to the angular momentum will produce zero angular impulse about the axle. Further, the angular momentum of the system must be conserved, since the impulse due to the snap of the string is of very short duration and the weight mg contributes negligibly in that time. The string is assumed to be inextensible, so .
Thus, we have , where . Solving for the angular speed, we get
The corresponding speed is given by
The final kinetic energy is given by
=
=
Topper's Solved these Questions
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - CHECKPOINT
18 Videos
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PROBLEMS
100 Videos
- RELATIVITYBOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
5 Videos
- RIGID BODY DYNAMICS-IIBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)
2 Videos
Similar Questions
A string is wrapped several times on a cylinder of mass M and radius R. the cylinder is pivoted about its adxis of block symmetry. A block of mass m tied to the string rest on a support positioned so that the string has no slack. The block is carefully lifted vertically a distance h, and the support is removed as shown figure.
a. just before the string becomes taut evalute the angular velocity ω0 of the cylinder ,the speed v0 of the falling body, m and the kinetic energy K0 of the system.
b. Evaluate the corresponding quanitities ω1,v1 and K1 for the instant just after the string becomes taut.
c. Why is K1 less than K0? Where does the energy go?
d. If M=m, what fraction of the kinetic energy is lost when the string becomes taut?
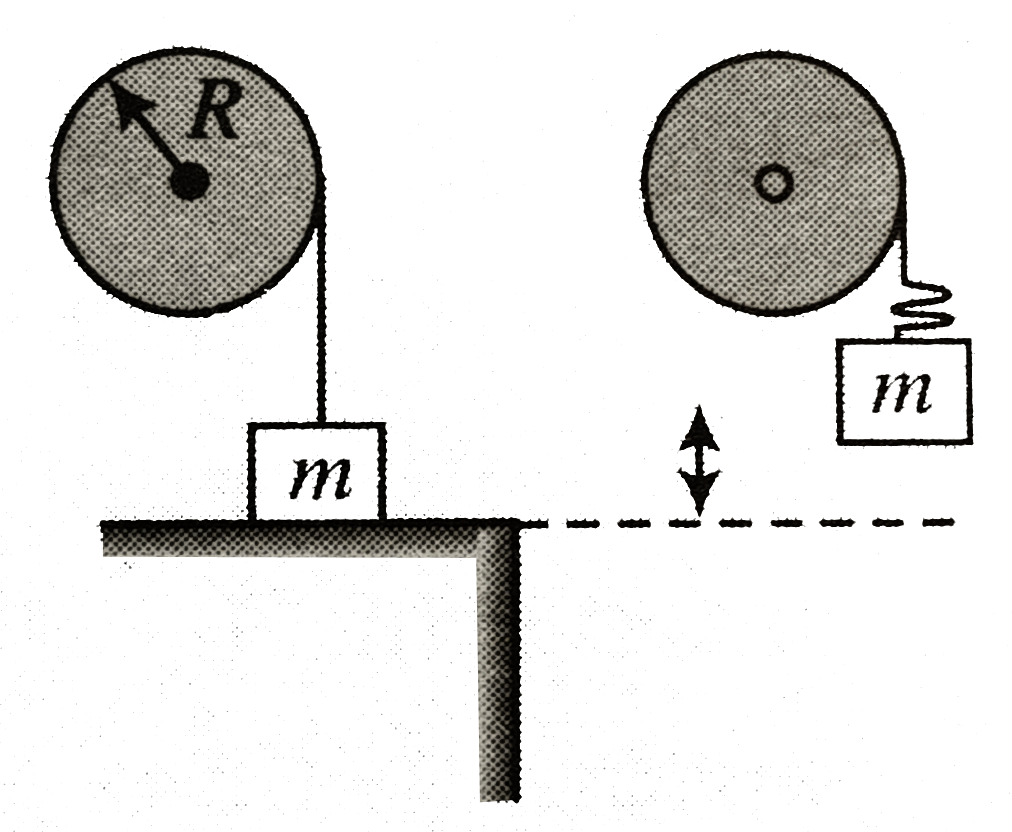
View SolutionA string is wrapped several times on a cylinder of mass M and radius R. the cylinder is pivoted about its adxis of block symmetry. A block of mass m tied to the string rest on a support positioned so that the string has no slack. The block is carefully lifted vertically a distance h, and the support is removed as shown figure.
a. just before the string becomes taut evalute the angular velocity ω0 of the cylinder ,the speed v0 of the falling body, m and the kinetic energy K0 of the system.
b. Evaluate the corresponding quanitities ω1,v1 and K1 for the instant just after the string becomes taut.
c. Why is K1 less than K0? Where does the energy go?
d. If M=m, what fraction of the kinetic energy is lost when the string becomes taut?
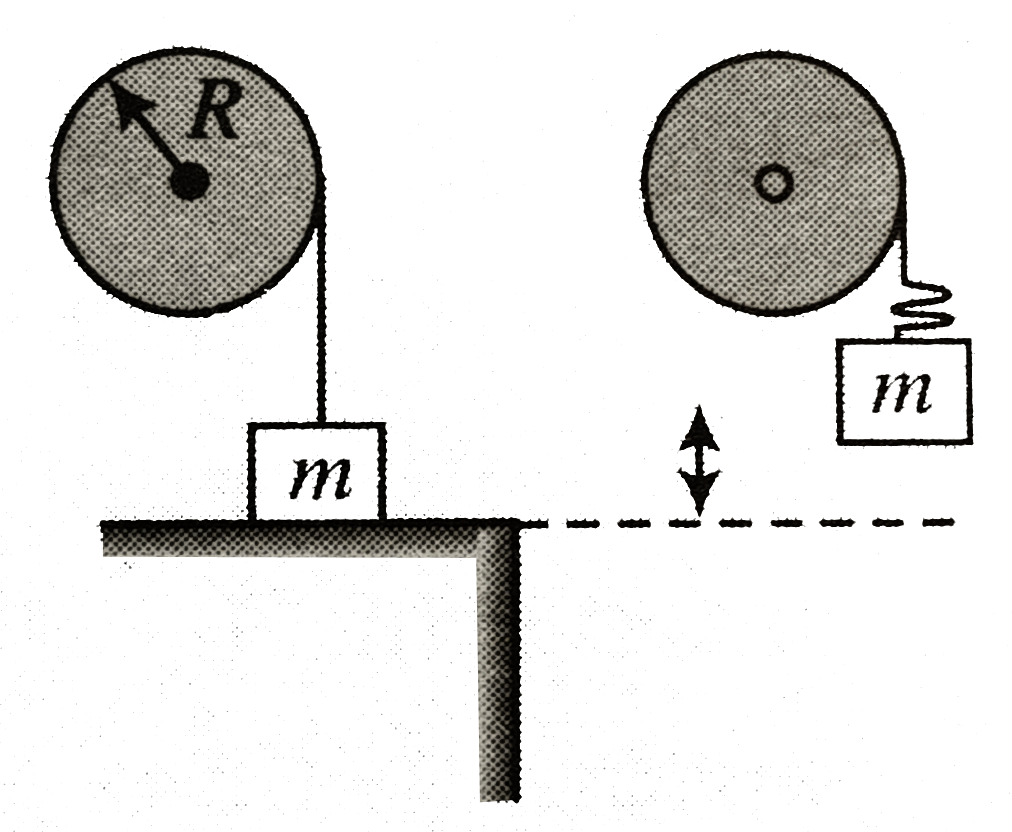
View Solution
Knowledge Check
A string is wrapped several time on a cylinder of mass M and radius R, the cylinder is pivoted about its axis of symmetery . A block mass of m tied to the string rests on support so that the string is black. The block is lifted upto a height h and the support is removed. (shown in figure)
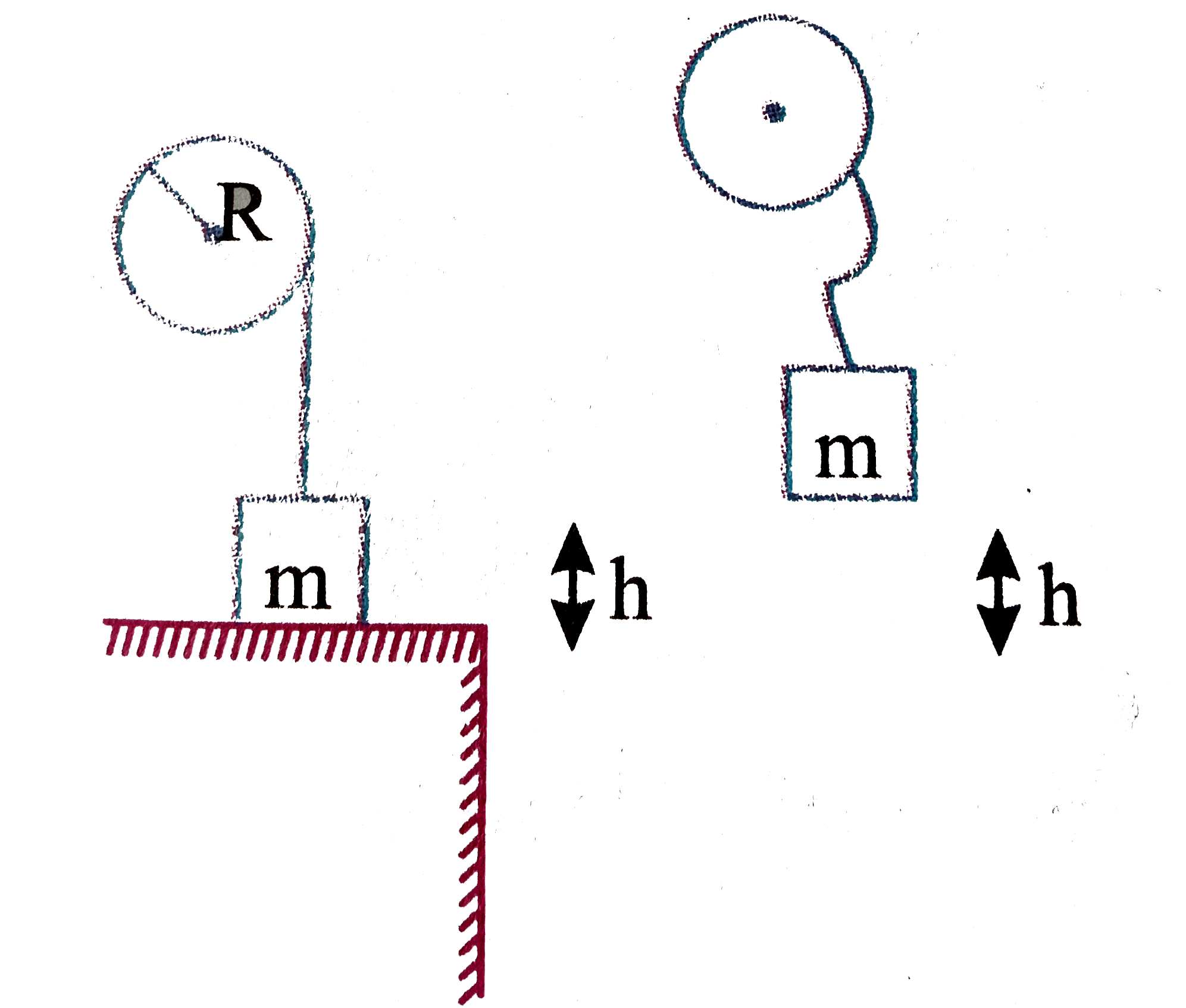
What is the angular velocity of cylinder just before the string becomes tautAzeroB√2ghRC√ghRD√ghRA string is wrapped several time on a cylinder of mass M and radius R, the cylinder is pivoted about its axis of symmetery . A block mass of m tied to the string rests on support so that the string is black. The block is lifted upto a height h and the support is removed. (shown in figure)
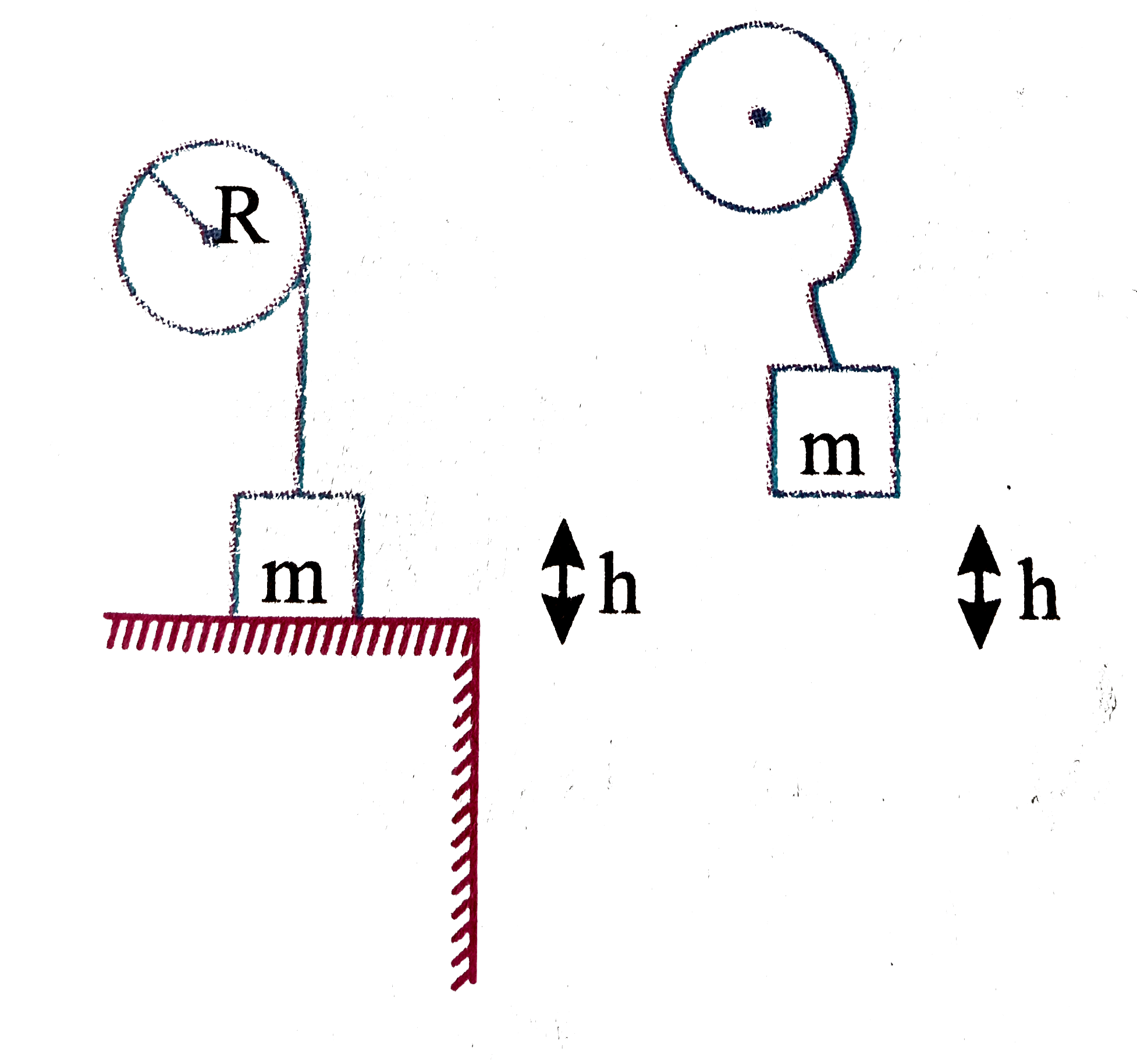
If M=m, what friction of KE is lost due to the jerk developed in the stringA1/2B2/3C1/3D1/4
A solid cylindrical pulley of mass m and radius R=10cm is hinged about its horizontal axis of symmetry. A light spring is wrapped around it, and small block of mass 'm' is suspended from the string. Now the block is lefted vertically by a distance h = 1.8 m and released. Just after the string becomes taut again, find the angular velocity of the cylinder in rad/s (Take g=10m/sec2)

View SolutionA solid cylindrical pulley of mass m and radius R=10cm is hinged about its horizontal axis of symmetry. A light spring is wrapped around it, and small block of mass 'm' is suspended from the string. Now the block is lefted vertically by a distance h = 1.8 m and released. Just after the string becomes taut again, find the angular velocity of the cylinder in rad/s (Take g=10m/sec2)

View SolutionA uniform disc of radius R and mass M is free to rotate only about its axis. A string is wrapped over its rim and a body of mass m is tied to the free end of the string as shown in the figure. The body is released from rest. Then the acceleration of the body is

View SolutionA uniform disc of radius R and mass M is free to rotate only about its axis. A string is wrapped over its rim and a body of mass m is tied to the free end of the string as shown in the figure. The body is released from rest. Then the acceleration of the body is

View SolutionA uniform disc of radius R and mass M is free to rotate only about its axis. A string is wrapped over its rim and a body of mass m is tied to the free end of the string as shown in the figure. The body is released from rest. Then the acceleration of the body is

View SolutionFind the moment of inertia of a solid cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder.
View Solution
