A horizontal plane supports a plank with a bar of mass m placed on it and attached by a light elastic non-deformed cord of length l0, to a point O. The coefficient of friciton between the bar and the plank is equal to m. The plank is slowly shifted to the right until the bar starts sliding over it. It occurs at the moment when the cord derivates from the vertical by an angle θ.
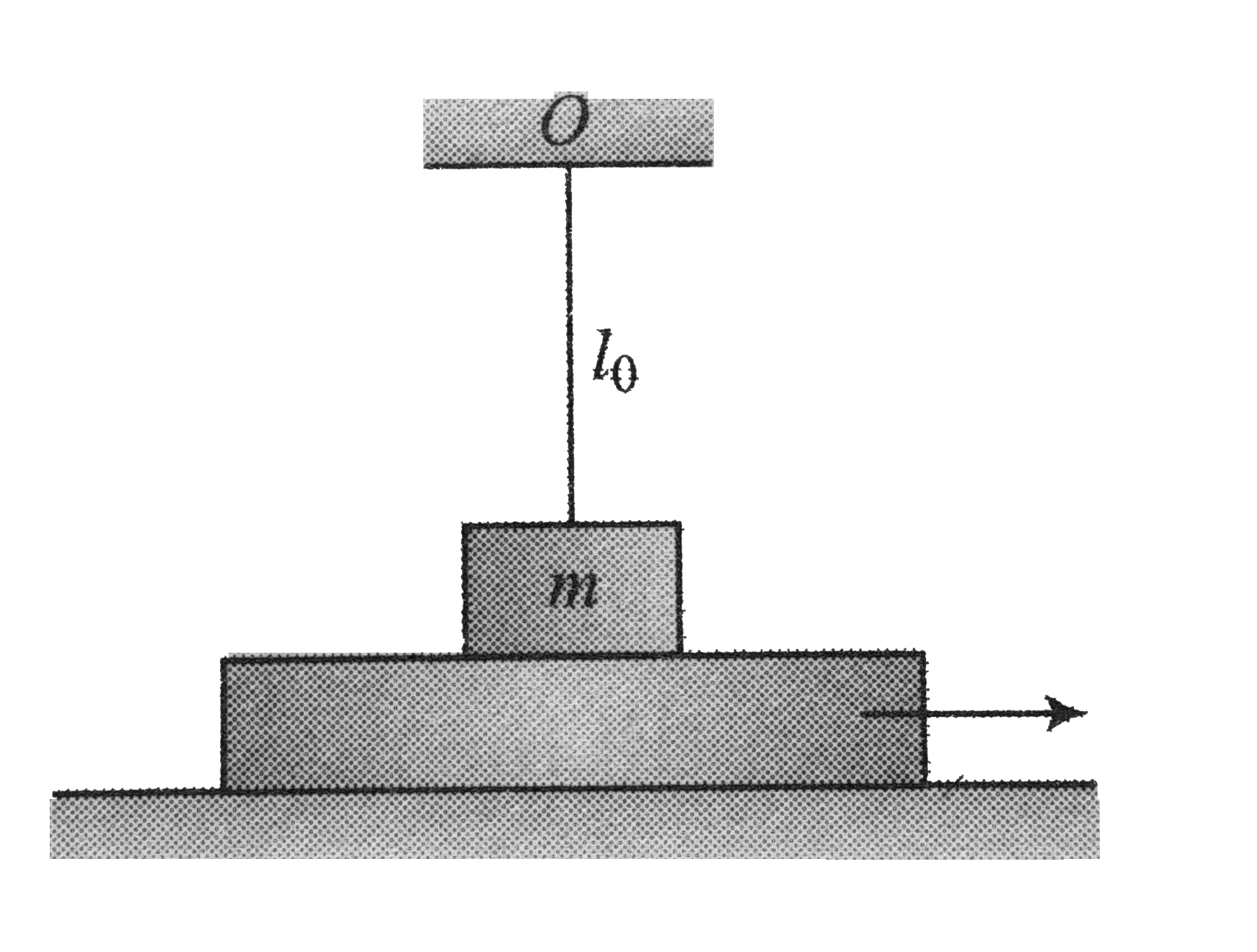
Find the work that has been performed by the moment by the frictional force acting on the bar in the reference frame fixed to the plane.
When the plank is pulled to the right, bar also moves to the right with the plank, and elastic cord elongates. Hence, a tension is developed in it.
Since the bar starts sliding over the plank when inclination of the elastic cord becomes equal to θ with the vertical, therefore at this moment, friction acting between the bar and the plank is at its limiting value.
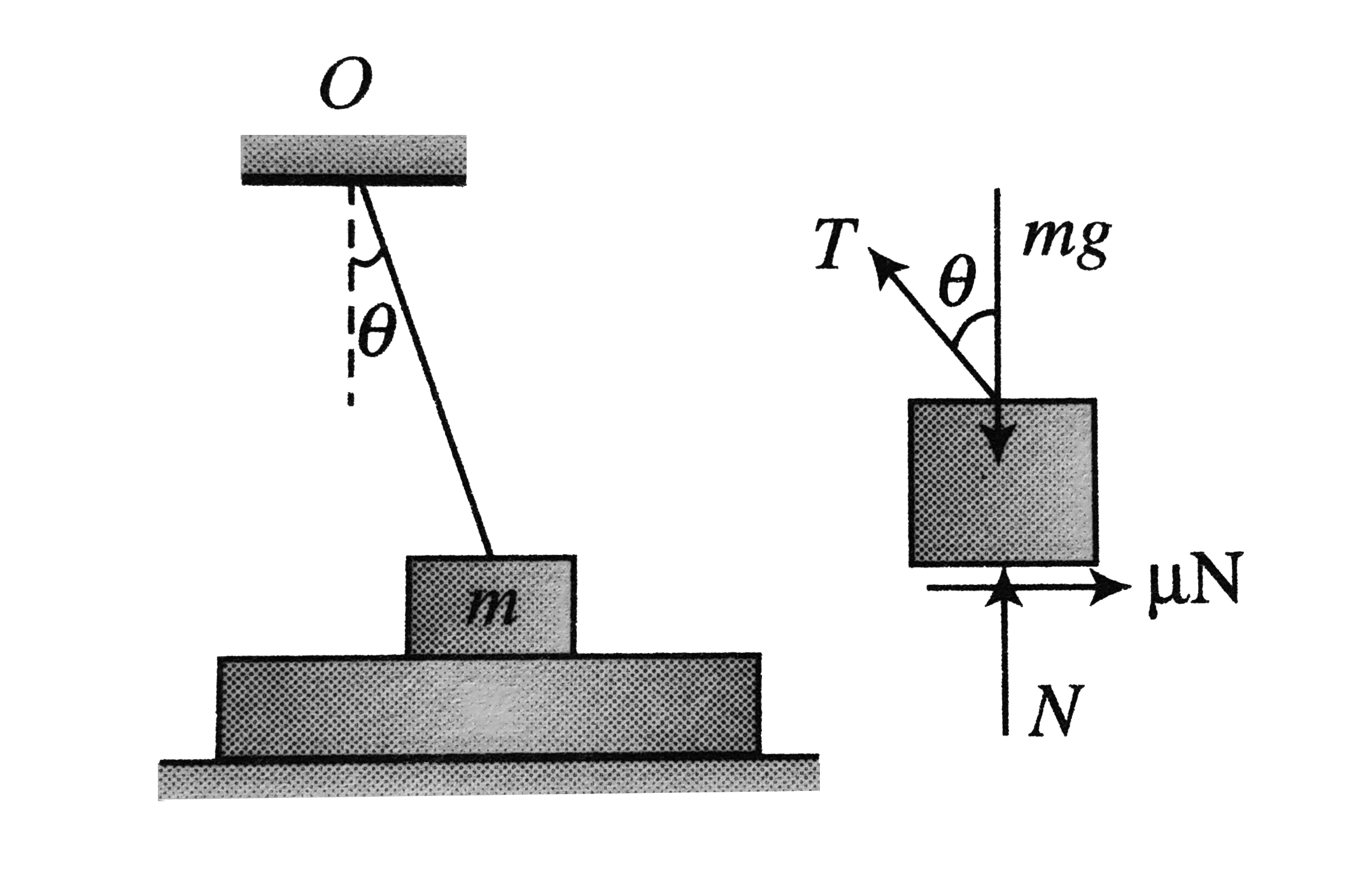
Let the force constant of the elastic cord be K. Then tension in it will be equal to T=KΔl, where Δl is elongation of the cord. It is equal to Δl=(l0secθ−l0)
T=K⋅l0(secθ−1)
Now considering FBD of the bar, for vertical equilibrium,
N+Tcosθ=mg
N=(mg−Tcosθ)
For horizontal equilibrium, μN=Tsinθ
μ(mg−Tcosθ)=Tsinθ
Substituing, T=K.l0(secθ−1)
K=μmgl0(secθ−1)(sinθ+μcosθ)
Since there is not slipping between the bar and plank up to this moment, therefore no energy is lost against friction.
Since the only force responsible for rightward displacement of the bar and hence for elongation of the cord is friction, therefore whole of the work done by the friction is used to elongate the cord. In fact it is stored in the cord in the form of its deformation energy.
Hence, the work that has been performed by the moment by the frictional force acting on the bar in the reference frame fixed to the plane is equal to 12K(Δl)2.
⇒W=12μmgl0(secθ−1)(sinθ+μcosθ)
Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Exercise 8.1
Explore 25 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Exercise 8.2
Explore 25 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Archives (integer)
Explore 4 Videos
- VECTORSBook:CENGAGE PHYSICS ENGLISHChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
A horizontal plane supports a plank with a block placed on it. A light elastic string is attached to the block, which is attached to a fixed point O. Initially, the cord is unstretched and vertical. The plank is slowly shifted to right until the block starts sliding over it. It occurs at the moment when the cord deviates from vertical by an angle θ=0∘. Work done by the force F equals

View SolutionA block of mass m is kept on a plank . The coefficient of friction between the plank and block is 1. The plank is slowly raised from one end so that it makes angle θ with horizontal . The forces of friction acting on the plank , when θ=30∘andθ60∘ are respectively,
View SolutionA plank with a bar placed on it performs horizontal harmonic oscillations with amplitude a=10cm. Find the coefficient of friction between the bar and the plank if the former starts sliding along the plank when the amplitude of oscillation of the plank becomes less than T=1.0s.
View SolutionA block is placed over a plank. The coefficient of friction between the block and the plank is μ=0.2. Initially both are at rest, suddenly the plank starts moving with acceleration a0=4m/s2. The displacement of the block in 1 is (g=10m/s2)
View SolutionA long plank of mass M is initially at rest on a frictionless surface. A small block with mass m and initial speed u0 slides on top of the larger plank. The coefficient of friction between the block and plank is μ
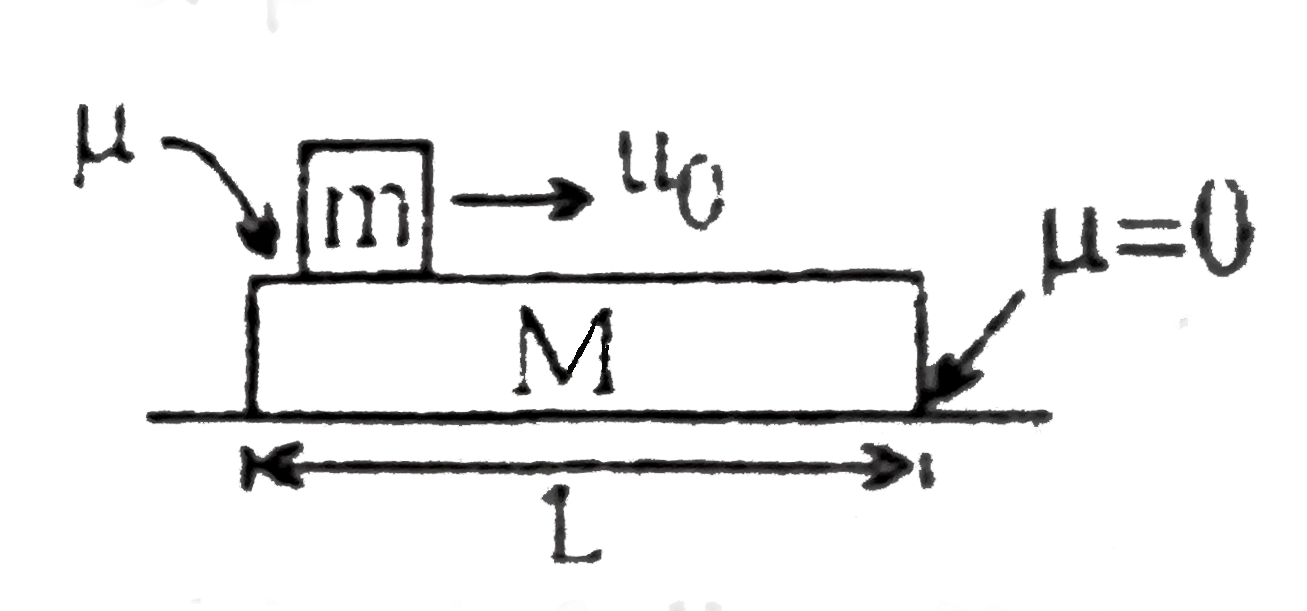
Net work done by friction if the top block falls off the plank after sliding over its length L is
View SolutionA block of mass m is gently placed over a massive plank moving horizontal over a smooth surface with velocity 10ms−1. The coefficient of friction between the block and the plank is 0.2. The distance travelled by the block till it slides on the plank is [g=10ms−2]
View SolutionA plank of mass M and length L is placed at rest on a smooth horizontal surface. A small block of mass m is projected with a velocity v0 from the left end of it as shown in figure. The coefficient of friction between the block and the plank is m, and its value is such that the block becomes stationary with respect to the plank before it reaches the other end.

a. Find the time and common velocity when relative sliding between the block and the plank stops.
b. Find the work done by the friction force on the block during the period it slides on the plank. Is the work positive or negative?
c. Calculate the work done on the plank during the same period. Is the work positive or negative?
d. Also, determine the net work done by friction, Is it positive or negative?
View SolutionBlock A of mass m rests on the plank B of mass 3m which is free to slide on a frictionless horizo-ntal surface. The coefficient of friction between the block and plank is 0.2. If a horizontal force of magnitude 2 mg is applied to the plank B, the acceleration of A relative to the plank and relative to the ground respectively, are:

View SolutionA plank of mass 10 kg and a block of mass 2 kg are placed on a horizontal plane as shown in the figure. There is no friction between plane and plank. The coefficient of friction between block and plank is 0.5 .A force of 60 N is applied on plank horizontally. In first 2 s the work done by friction on the block is

View SolutionA block is kept on a rough horizontal plank. The coefficient of friction between the block and the plank is 12. The plank is undergoing SHM of angular frequency 10 rad/s. The maximum amplitude of plank in which the block does not slip over the plank is (g= 10 m/s2)
View Solution