A horizontal tube of length I closed at both ends contains an ideal gas of molecular weight M, The tube is rotated at a constant angular velocity ω about a vertical axis passing through an end. Assuming the temperature to be uniform and constant, show that
p2=p1eMω2l22RT,
where p2 and p1 denote the pressures at the free end and the fixed end respectively.
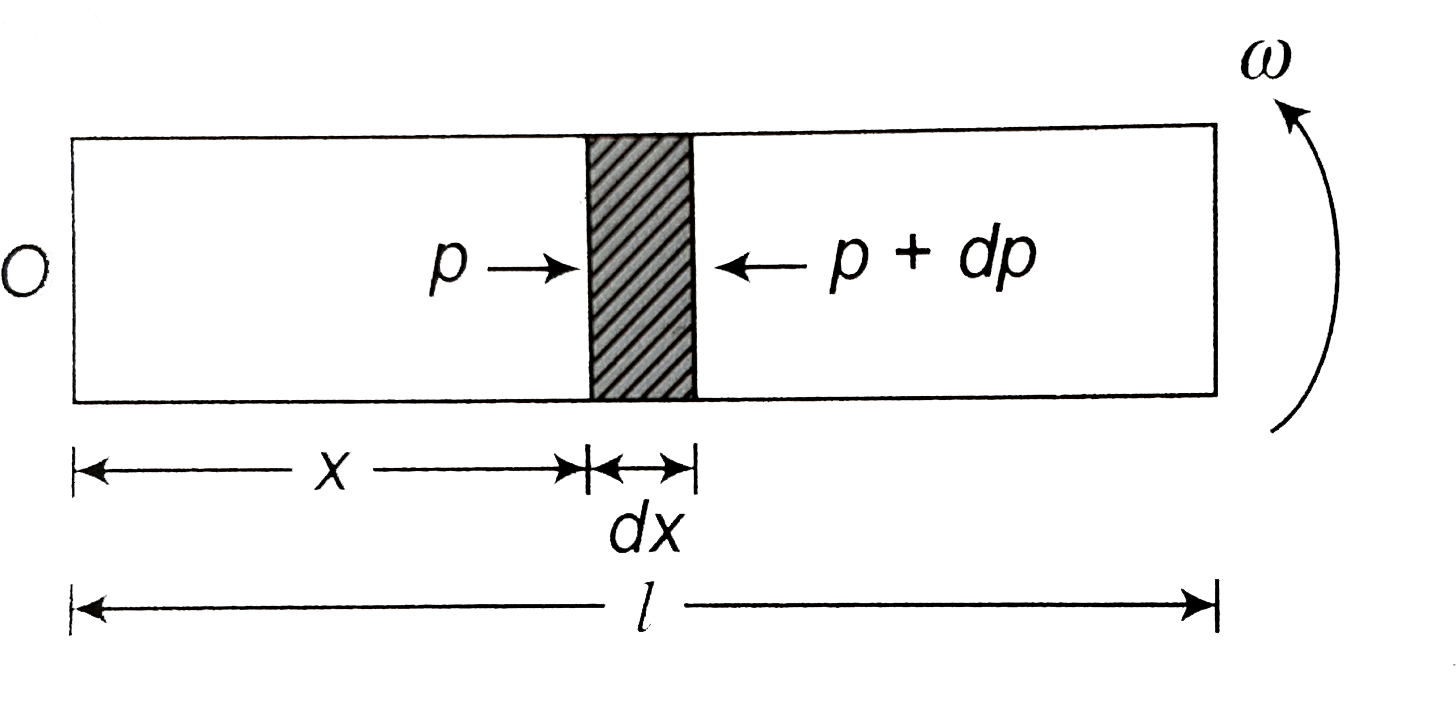
Consider an element of the gas between x and x+dx from O.
Let p and p+dp be the pressures as shown.
The force acting on the element towards the centre
=(p+dp−p)A=dpA,
A: area of X-section
This elements is moving in circle of radius x
dpA=dmω2x (i)
pV=nRT
pAdx=dmMRT
dm=MpARTdx (ii)
From (i) and (ii)
dpA=MpARTdxω2x
p2∫p1dpp=Mω2RTl∫0xdx
1np2p1=Mω2l22RT
p2=p1eMω2l2RT
Topper's Solved these Questions
Similar Questions
A horizontal tube of length I closed at both ends contains an ideal gas of molecular weight M, The tube is roatated at a constant angular velocity ω about a vertical axis passing through an end. Assuming the temperature to be uniforme and constant, show that
p2=p1eMω2l22RT,
where p_(2) and p_(1)denote the pressures at the free end and the fixed end respetively.View SolutionA horizontally oriented tube AB of length l rotates with a constant angular velocity ω about a stationary vertical axis OO′ passing through the end A (figure). The tube is filled with an ideal fluid. The end A of the tube is open, the closed end B has a very small orifice. Find the velocity of the fluid relative to the tube as a function of the column "height" h.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A12mω2xB12mω2(1−x2l)C12mω2l(1−x2l2)D12mω2l[1−xl] - Question 2 - Select One
For an L shaped conducting rod placed in an uniform magnetic field →B rotating with constant angular velocity ω about an axis passing through one of its ends A and normal to the plane of the conductor induced emf
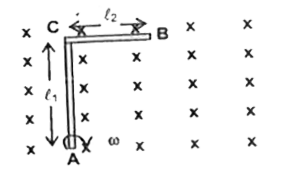 Aacross AC equals ωBl21Bacross AC equals 12ωBl21Cacross BC equals zeroDNone of the above is correct
Aacross AC equals ωBl21Bacross AC equals 12ωBl21Cacross BC equals zeroDNone of the above is correct - Question 3 - Select One
A thin uniform copper rod of length l and cross-section area A and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. The elongation of the rod will be
Amω2l26AYBmω2l23AYCmω2l2AYDmω2l22AY
A conducting rod of length l is rotating with constant angular velocity ω about point O in a uniform magnetic field B as shown in the figure . What is the emf induced between ends P and Q ?
 View Solution
View SolutionA horizontal tube with closed ends is rotated with a constant angular velocity ω about a vertical axis passing through one of its ends. The tube contains carbon dioxide at a temperature T=300K. The length of the tube is l=100cm. Find the value ω at which the ratio of molecular concentrations at the opposite ends of the tube is equal to η=2.0.
View SolutionA horizontal cylinder closed from one end is rotated with a constant angular velocity ω about a vertical axis passing through the open end of the cylinder. The outside air pressure is equal to p0, the temperature to T, and the molar mass of air to M. find the air pressure as a function of the distance r from the rotate axis. The molar mass is assumed to be independent of r.
View SolutionA uniform stick of length l and mass m lies on a smooth table. It rotates with angular velocity ω about an axis perpendicular to the table and through one end of the stick. The angular momentum of the stick about the end is
View SolutionA copper rod of length l is rotated about one end perpendicular to the uniform magnetic field B with constant angular velocity ω . The induced e.m.f. between its two ends is
View Solution

