A launch travels across a river from a point A to a point B of the opposite bank along the line AB forming angle ∝ with the bank. The flag on the mast of the launch makes an angle β with its direction of motion. Determine the speed of the launch w.r.t. the bank. The velocity of wind is u perpendicular to the stream.
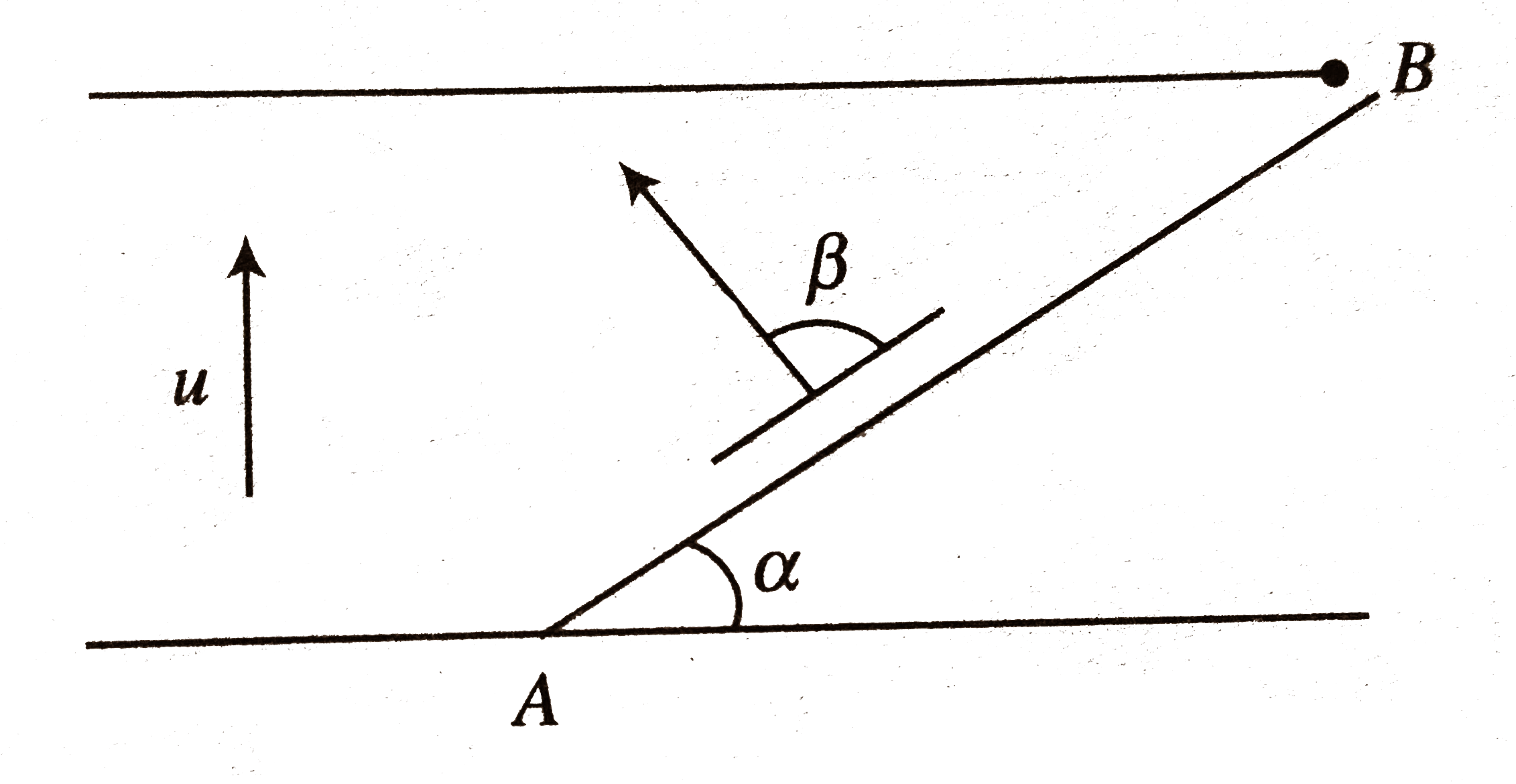 .
.
The correct Answer is:usin(∝+β−π/2)sinβ.
Flag on a launch in the direction of the wind relative to the launch. Therefore, β is the angle made by relative velocity of the wind in relation to the launch.
→VWind,Earth=→u=uˆj
→vLaunch,Earth=→v
=vcos∝ˆi+vsin∝ˆj
→VWind, Launch=→u−→v
=−vcos∝ˆi+(u−vsin∝)ˆj
tan(∝+β)=u−vsin∝−vcos∝
−vtan(∝+β)cos∝=u−vsin∝
v[sin∝−cos∝tan(∝+β)]=u
v=−ucos(∝+β)sinβ=usin(∝+β−π/2)sinβ.
 .
.
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Single Correct
76 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Multiple Correct
11 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.4
11 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
A swimmer starts to swim from point a to cross a river. He wants to reach point B on the opposite side of the river. The line AB makes an angle 60∘ with the river flow as hown. The velocity of the swimmer in still water is same as that of the water

(i) In what direction should he try to direct his velocity ? Calculate angle between his velocity anf river velocity.
(ii) Find the ratio of the time taken to cross the river in this situation to the minimum time in which he can cross this river.
View SolutionA swimmer starts to swim from point a to cross a river. He wants to reach point B on the opposite side of the river. The line AB makes an angle 60∘ with the river flow as shown. The velocity of the swimmer in still water is same as that of the water
(i) In what direction should he try to direct his velocity ? Calculate angle between his velocity ? Calculate angle between his velocity and river velocity.
(ii) Find the ratio of the time taken to cross the river in this situation to the minimum time in which he can cross this river.

View Solution
Knowledge Check
A man in a row boat must get from point A to point B on the opposite bank of the river (see figure).The distance BC=a.The width of the river AC=b.At what minimum speed u relative to the still water should the boat travel to reach the point B?The velocity of flow of the river is v0
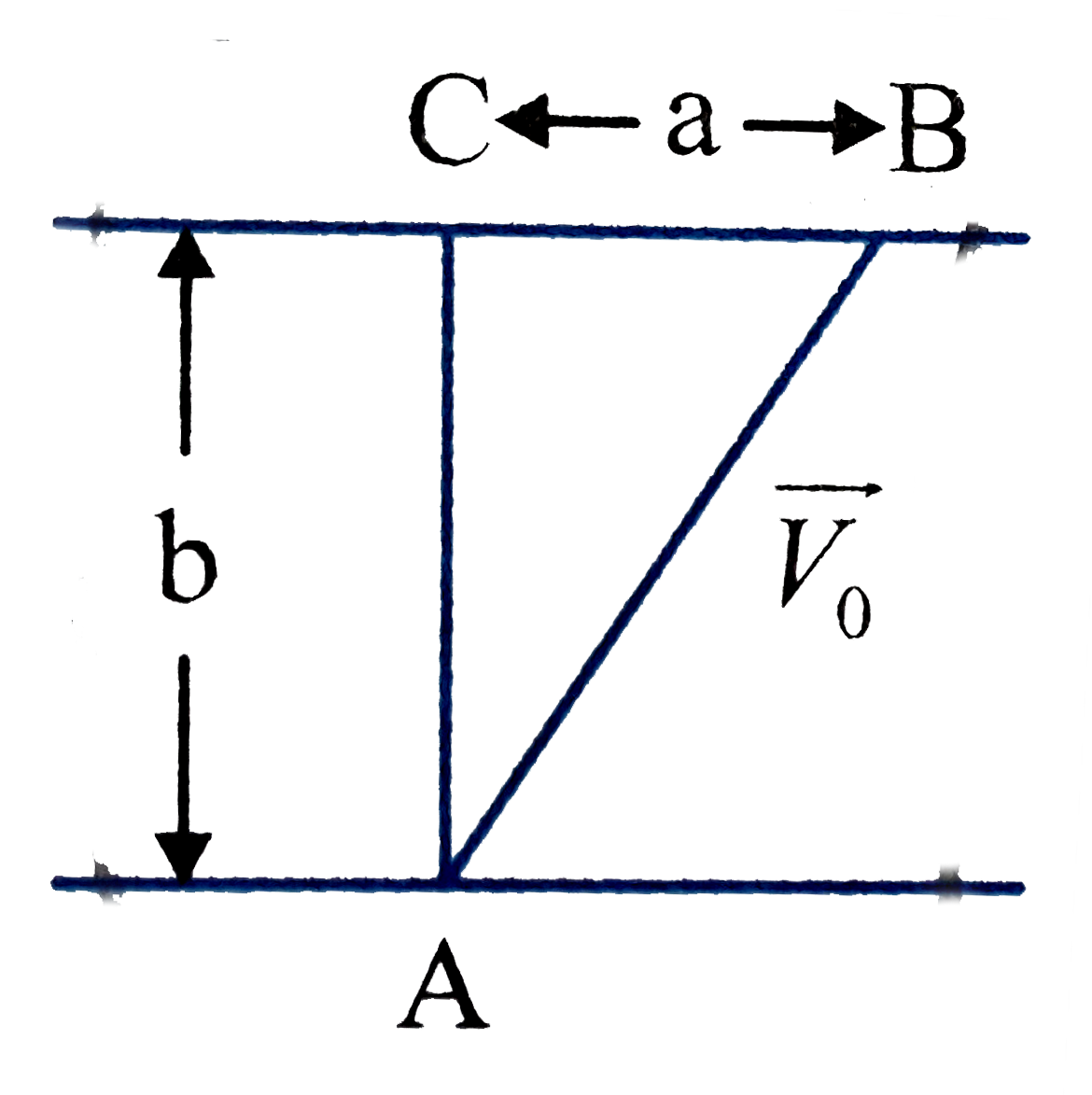 Av0b√a2+b2Bv0a√a2+b2Cv0b√2aDv0a√2b
Av0b√a2+b2Bv0a√a2+b2Cv0b√2aDv0a√2bA person aiming to reach exactly opposite point on the bank of a stream is swimming with a speed of 0.6 m/s at an angle of 120∘ with the direction of flow of water . The speed of water in the stream is
A0.3 m/sB0.5 m/sC1.0 m/sD0.433 m/sA person aiming to reach the exactly opposite point on the bank of a stream is swimming with a speed of 0.5ms at an angle of 120∘ with the direction of flow of water. The speed of water in the stream is
A1msB0.5msC0.25(m)/(s)D0.433ms
The velocity of water current in a river changes with distance along the perpendicular to the river according to the law u=2u0dy for 0≤y≤d2 where u0= velocity in the mid-stream d= width of the river =2u0d(d−y) for d2≤y≤d.
A boat travels from a point O on one block of the river to the opposite bank and its steering angle is constantly changed to keep its relative velocity perpendicular to the river current. Calculate the time in which the boat will reach the other bank. The velocity of the boat in still water is u0.
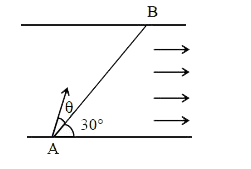
View SolutionA swimmer wants to cross a river from point A to point B. Line AB makes an angle of 30∘ with the flow of river. Magnitude of velocity of the swimmer is same as that of the river. The angle θ with the line AB should be _________ ∘, so that the swimmer reaches point B.
View SolutionTwo bodies A and B are moving with velocities vA and vB, making an angle θ with each other. Determine the relative velocity of A w.r.t. B. What will be the relative velocity when the two bodies move in opposite directions ?
View SolutionFrom a point A on bank of a channel with still water a person must get to a point B on the opposite bank.All the distances are shown in figure.The person uses a boat to travel across the channel and then walks along the bank of point B.The velocity of the boat is v1 and the velocity of the walking person is v2.Prove that the fastest way for the person to get from A to B is to select the angles α1 and α2 in such a manner that
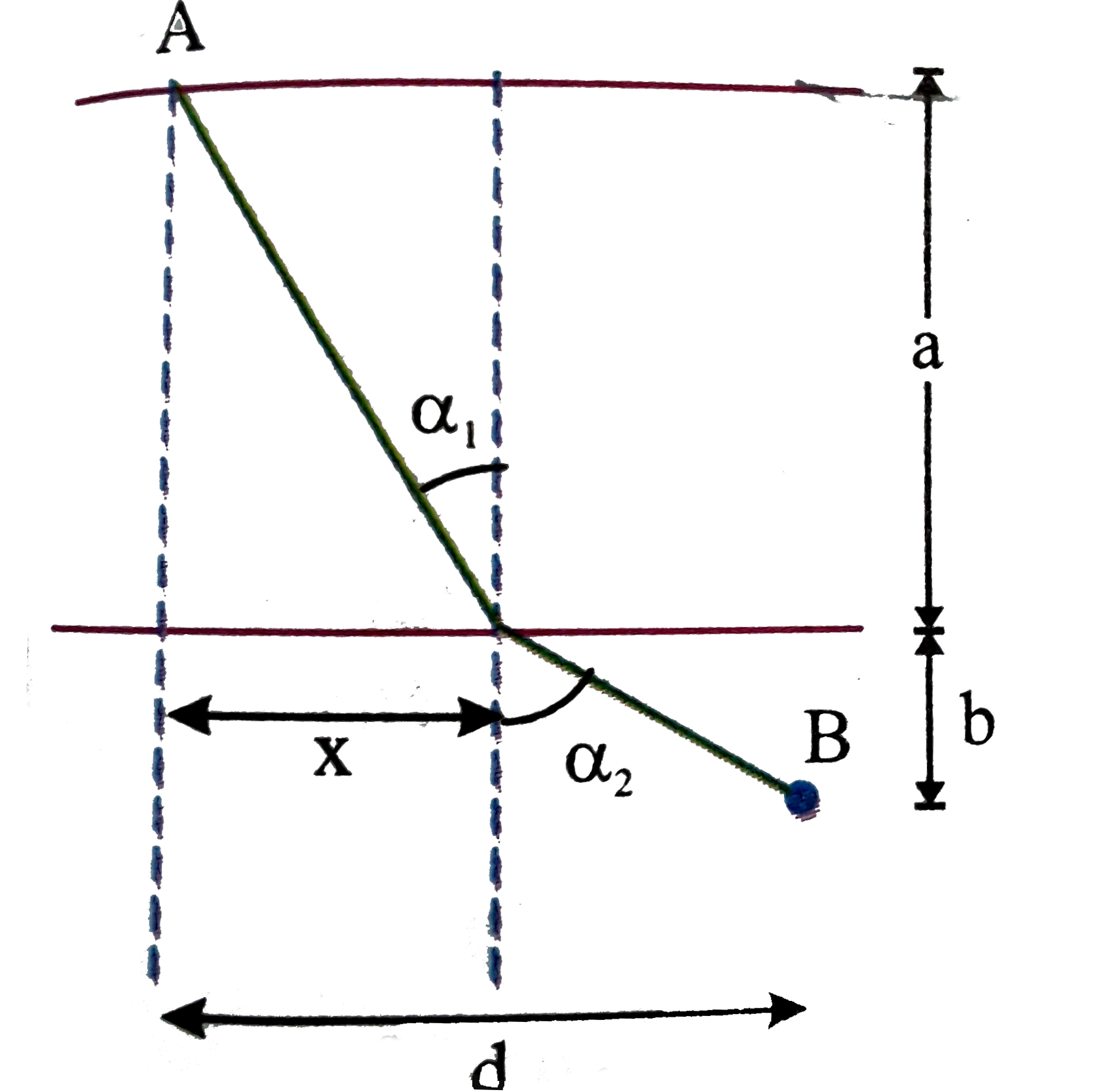
View SolutionPerson aiming to reach the exactly opposite point on the bank of a stream is swimming with a speed of 0.5ms−1 at an angle of 120∘ with the direction of flow of water.The speed of water in the stream is
View Solution
