A light source S is placed at the centre of a glass sphere of radius R and refractive index μ. The maximum angle θ with the x-axis (as shown in the figure) an incident light ray can make without suffering total internal reflection is

cos−1(1μ)
sin−1(1μ)
tan−1(1μ)
there will never be total internal reflection
The correct Answer is:D
∠i=0∘ for all values of θ, as the rays fall normal to sphere at all point.
Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Single Correct Option
3 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - more than one correct option
1 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Subjective Questions
8 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
- SEMICONDUCTORSBOOK - DC PANDEYCHAPTER - SEMICONDUCTORSEXERCISE - Subjective
12 Videos
Similar Questions
The refractive index of a prism is μ. Find the maximum angle of the prism for which a ray incident on it will be transmitted through other face without total internal reflection.
View SolutionA light rays is incident on a prism of prism angle A and refractive index μ. Show that the smallest value of the angle of incidence for which the reflected ray does not suffer total internal reflection at the second face, i.e. just comes out of it, is given by
i=sin−1[(μ2−1)1/2sinA−cosA].
View Solution
Knowledge Check
Inside a solid glass sphere of radius R, a point source of light lies at a distance x(x<R) from centre of the sphere. The solid is surrounded by air of refractive index 1. The maximum angle of incidence for rays incident on the spherical glass air interface directly from the point soure is:
Acos−1xRBsin−1xRCcos−1√xRDsin−1√xRA ray of lighyt is incident at an angle I on a glass slab of refractive index μ. The angle between reflected and refracted light is 90∘ Then the relationship between I and μ is
Ai=tan−1(1μ)BtanI=μCsinI=μDcosI=μA ray of light is incident on a glass slab of refractive index 1.5, making an angle of 40∘ with the surface. The angle of refraction in glass is
A40∘B30∘42'C50∘D60∘
Cross section of a light pipe is shown in the following figure :

Inner core is material of refractive index 1.68 and its outer covering is a material of refractive index 1.44. Find the maximum angle at which the ray can be incident with the axis of pipe for which total internal reflection occurs inside the pipe.
View SolutionConsider the situation shown in figure. Find the maximum angle theta for which the light suffers total internal reflection at the vertical surface.
View SolutionA ray of light is incident on the surface of a glass plate of refractive index 1.6 at polarzing angle. Calculate the angles of reflection and refraction.
View SolutionLight incidence on a sphere of refractive index √3 placed in a air as shown in Figure. Find the angle (θ)in degree between emergent ray and reflected ray.
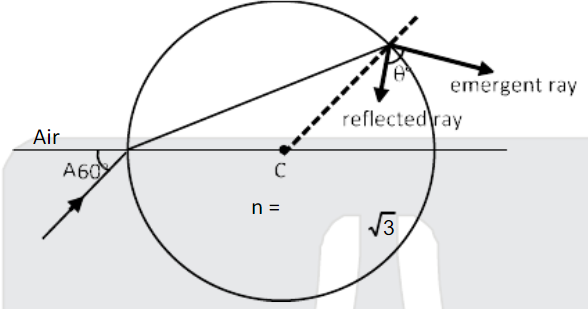
View SolutionA light ray is incident on a glass sphere of reflective index μ=√3 at an angle of incidence 60∘ as shown in Fig. Find the angles r, r′ e and the total deviation after two refractions.
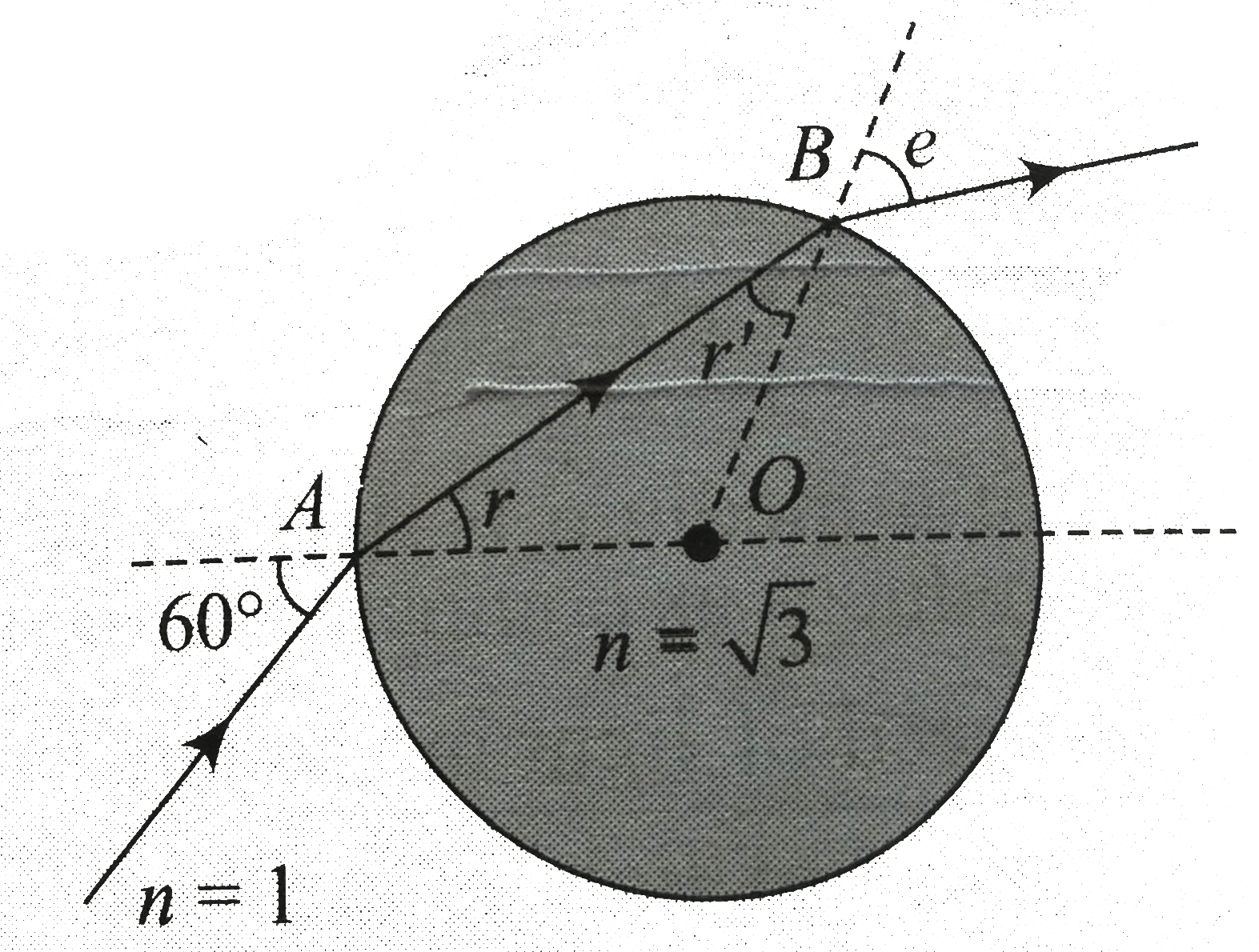
View Solution
