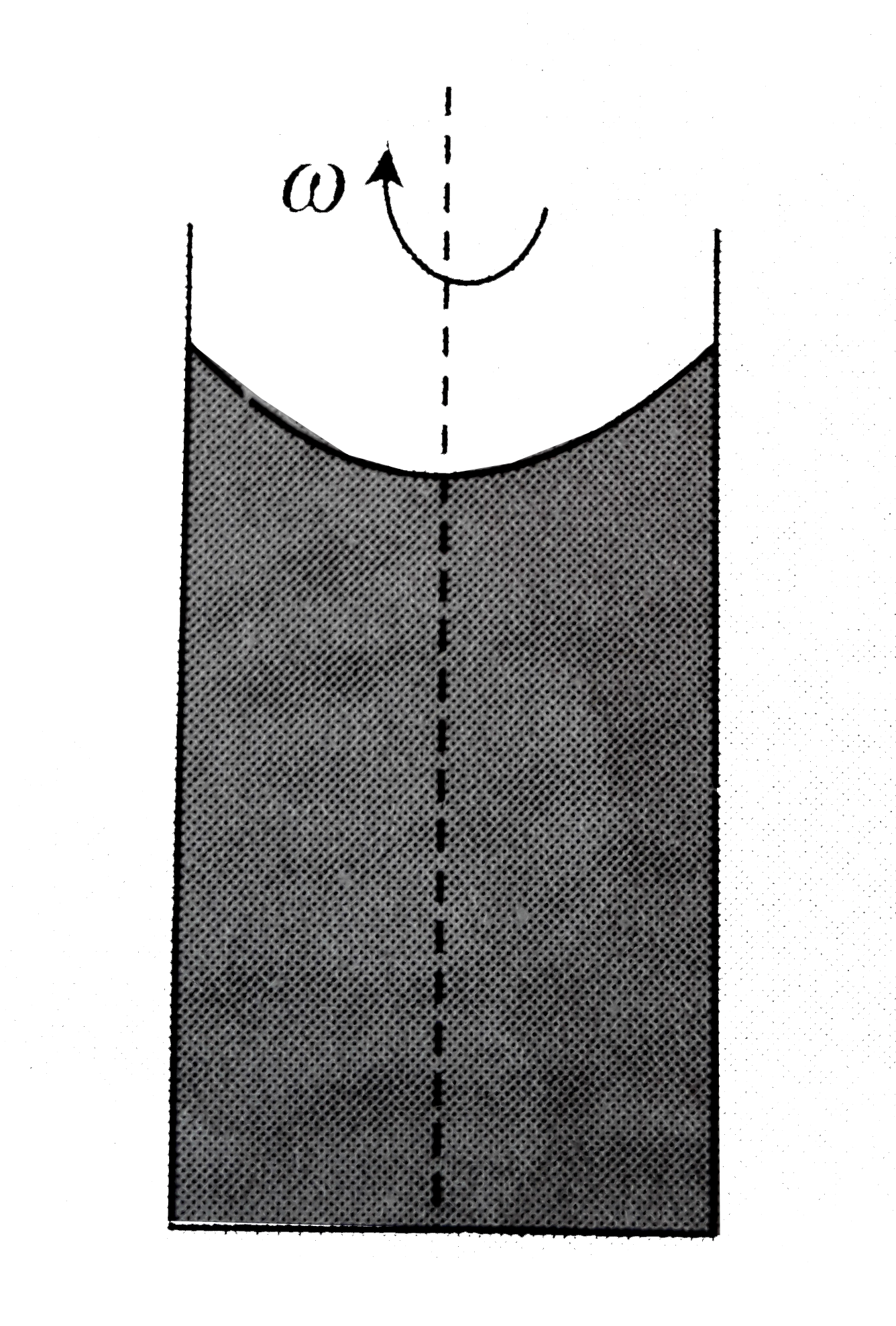
A liquid of density ρ is in a vessel rotating with angular velocity ω as shown in figure. If P0 is the atmospheric pressure, find pressure at a radial distance r from the axis.
 .
.
Consider a fluid particle A of mass at position (x,y)
Forces acting on particle A are
(i) pseudo force (mω2x)
(ii) weight (mg)
Net force on A should be perpendicular to the free surface (in equilibrium) [liquid cannot take shear stress]
tanθ=mω2xmg=ω2xg
dydx=ω2xg
∫y0dy=ω2g∫x0xdx
y=ω2x22g
At x=r,y=ω2r2g
P=P0+ρgy=P0+ρω2r22=P0+12ρv2(sincev=rω).
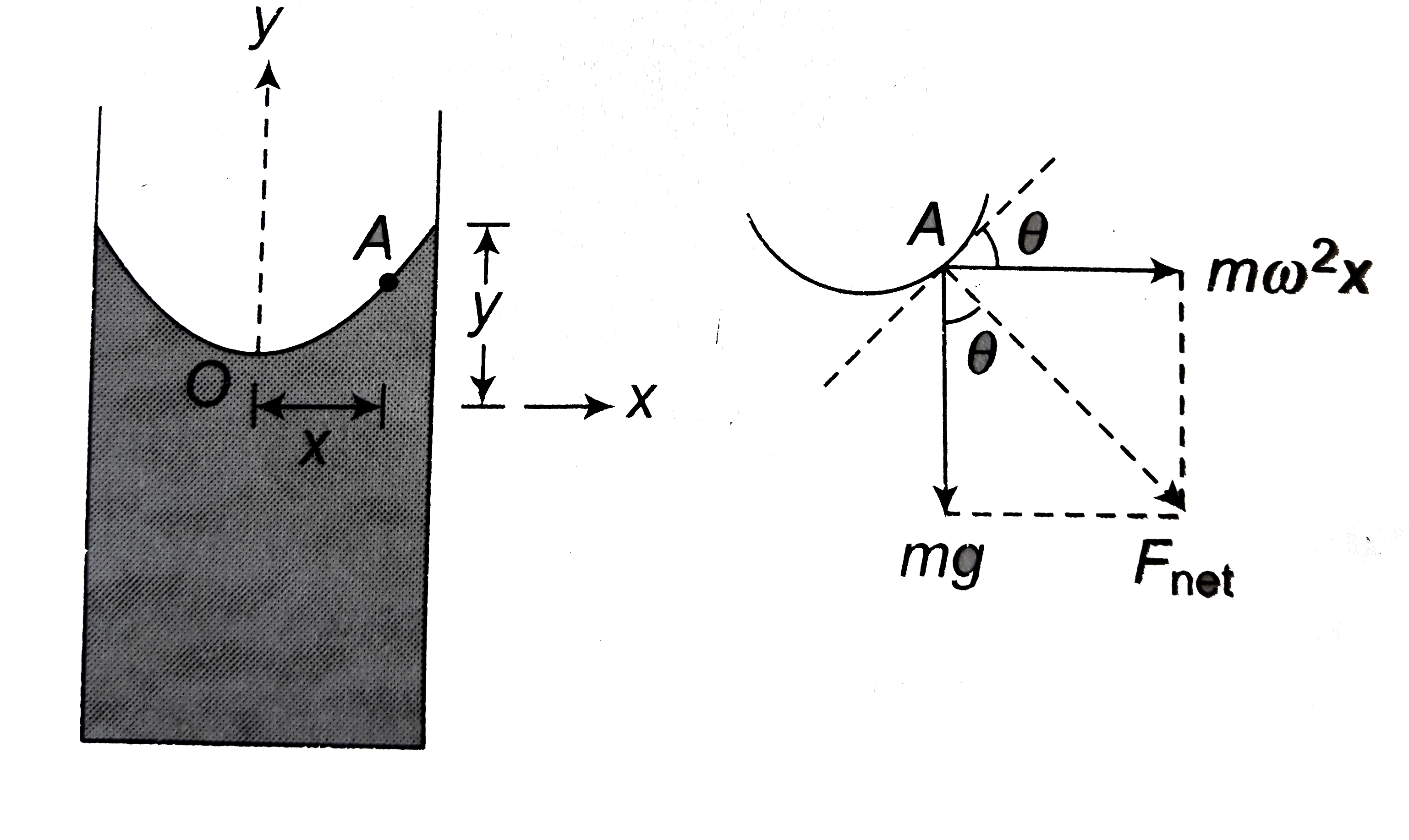
Topper's Solved these Questions
Similar Questions
A liquid of density ρ is in a bucket that spins with angular velocity 'ω' as shown in figure. Prove that the free surface of the liquid has a parabolic shape. Find equation of this.
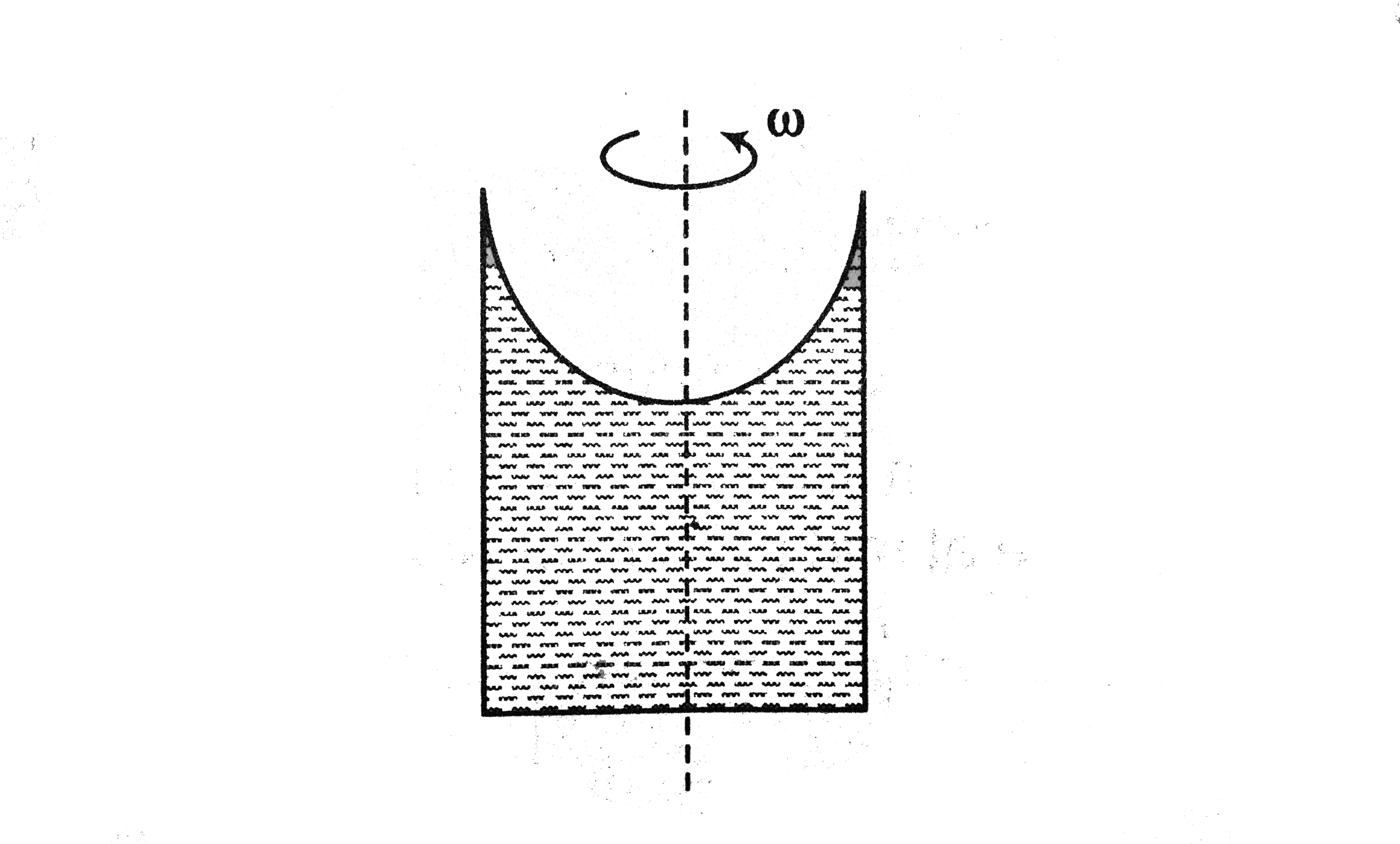 .
.
View SolutionA liquid of density 'ρ' is rotated with an angular speed 'ω' as shown in figure. Using the pressure equation concept find the equation of free surface of the liquid.
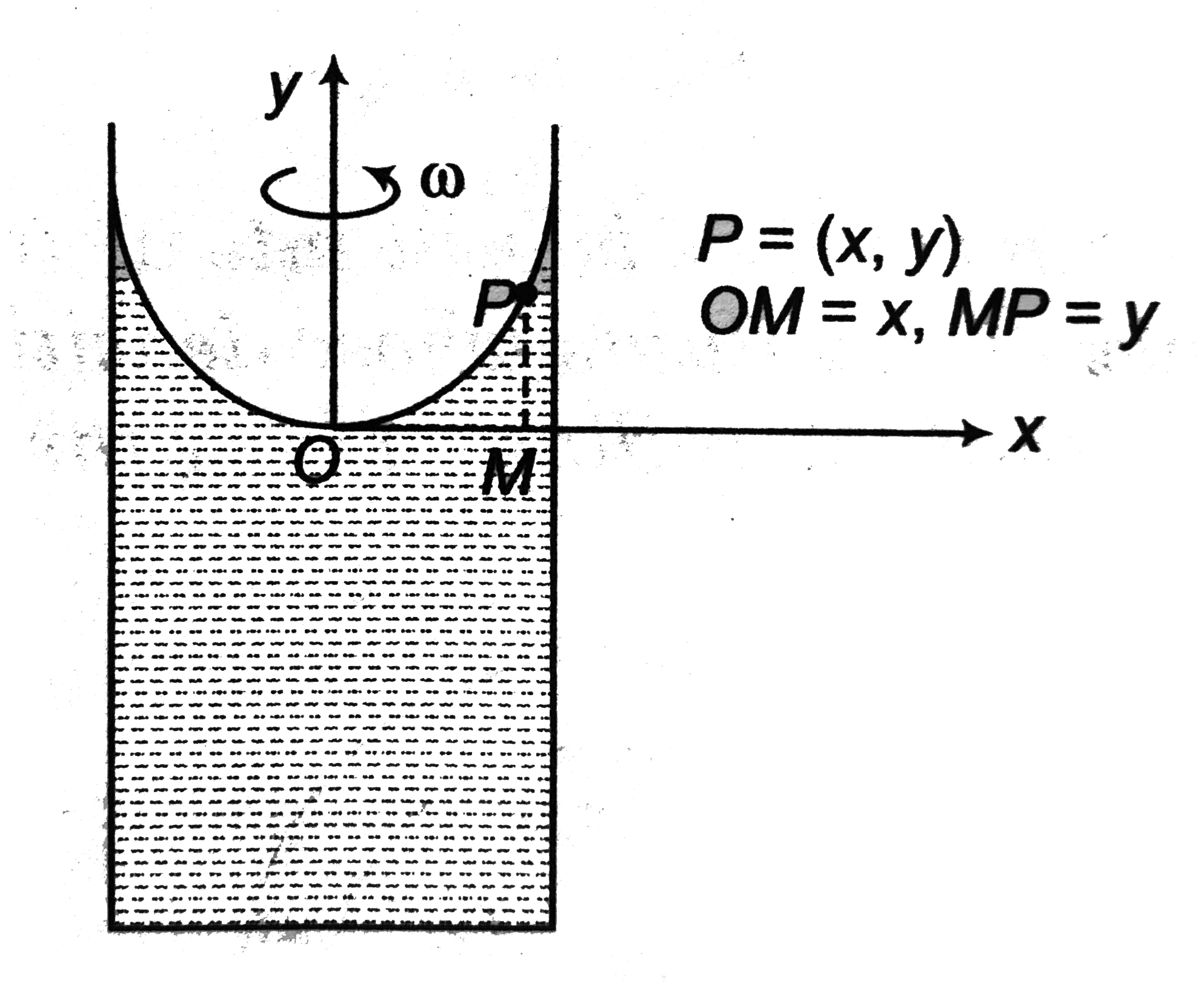 .
.
View Solution
Knowledge Check
A rod is rotating with angular velocity ω about axis AB. Find cosθ.
 Ag2lω2Bglω2C2g(lω)2D3g2lω2
Ag2lω2Bglω2C2g(lω)2D3g2lω2A small tank of cylindrical shape and of radius R is containing a liquid of density σ. On rotating the vessel about its axis with angular velocity ω, the liquid rises at the sides of vessel through height h. P1andP2 are pressure at sides and at the centre of tank respectively, then
AP1>P2BP1=P2CP2>P1Dh=R2ω22gA liquid of density ρ has to spray with help of aspirator pump at height H from liquid level as shown in figure. If gauge pressure inside bulb is P and density of air is σ then velocity of air in tube AB is
 A{P+ρgHσ2}12B{P−ρgHσ2}12C{P+αgHσ2}12D{P+αgHσ}12
A{P+ρgHσ2}12B{P−ρgHσ2}12C{P+αgHσ2}12D{P+αgHσ}12

A liquid of density ρ is rotated by an angular speed ω as shown in figure, Using the concept of pressure equation, find a relation between h1,h2,x1 and x2.
View SolutionA wheel is rotating with uniform angular velocity →ω. What is the nature of the graph between tangential speed at different points of the wheel and their radial distances from the axis?
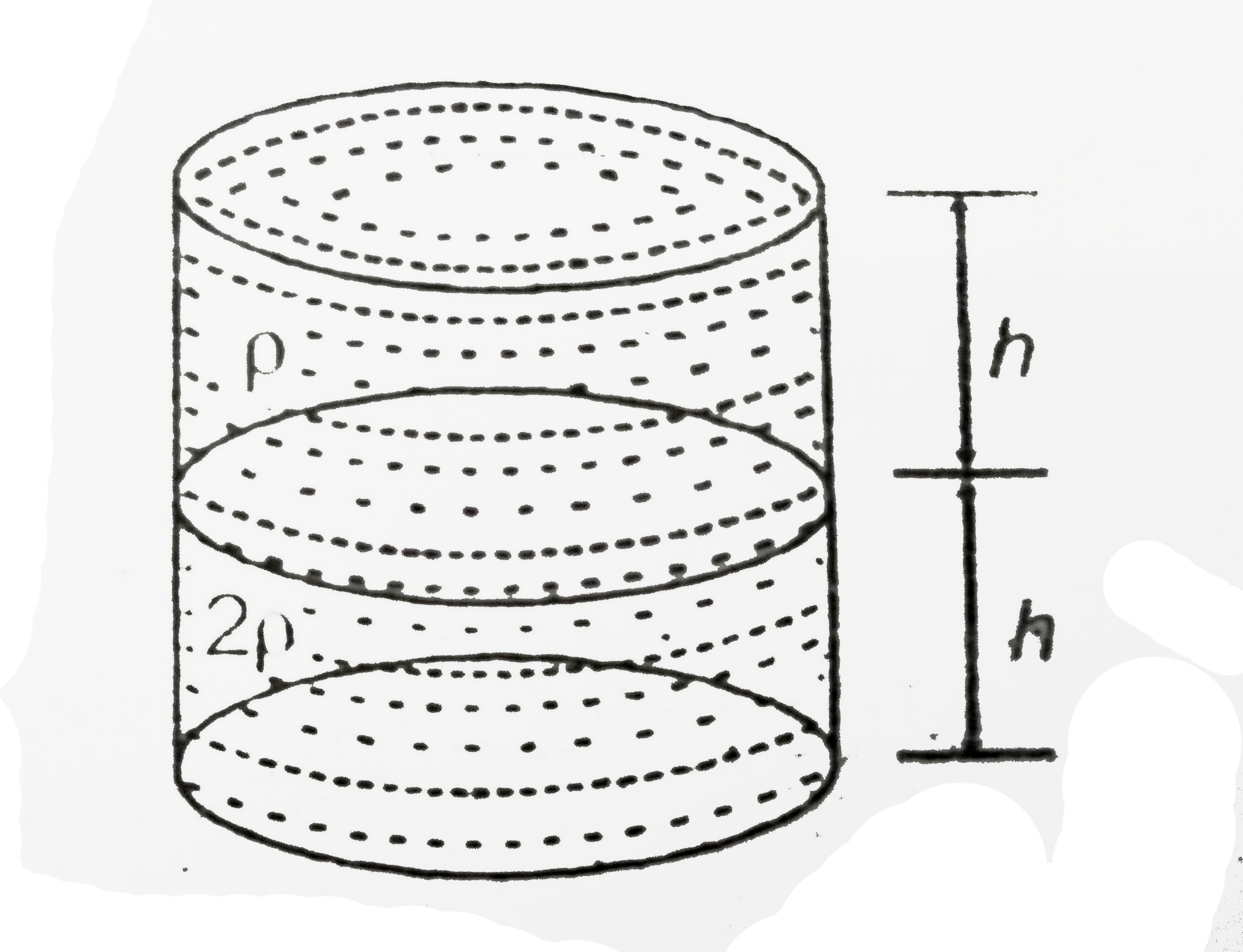
View SolutionA container of cross-section area A resting on a horizontal surface, holds two immiscible and incompressible liquid of densities ρand2ρ as shown in figure. The lower density liquid is open to the atmosphere having pressure P0. The pressure at the bottom of the container is
View SolutionLength of a horizontal arm of U-tube is L and ends of both the vertical arms are open to atompsheric pressure P0, A liquid of density ρ is poured in the tube such that liquid just fills the horizontal part of the tube as shown in figure . Now one end of the opened ends is sealed and the tube is then rotated about a vertical axis passing through the other vertical arm with angular speed ω0. if length of each vertical arm is a and in the sealed end liquid rises to a height y, find pressure in the sealed tube during rotation.
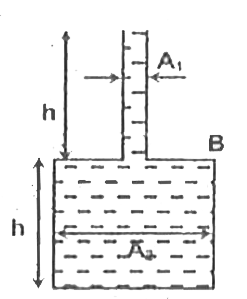
View SolutionThe vessel shown in the figure has two sections of area of cross - section A1andA2 .A liquid of density ρ fills both the section upto a height h in each . Consider atmospheric pressure P0 also . Find
(a) the pressure at the base of vessel .
(b) the force exerted by the liquid on the base of the vessel .
(c ) the downward force exerted by the walls of the vessel at the level B
View Solution
