a long coaxial cable consists of two thin-walled conducting cylinder carries a steady current $0.1 A$ , and the outer cylinder provides the return path for that current. The current produced a magnetic field between the two cylinders. Find the energy stored in the magnetic field for length $5 m$ of the cable. Express answer in Nj (use $1 n 2 = 0.7$ ).

Video Solution

Text Solution

Verified by Experts

The correct Answer is:7

The magnetic field inside is only due to the current of the inner cylinder.
$B = \frac{μ_{0} i}{2 π r}$
Magnetic field energy density is not uniform in the space between the cylinders. At a distance $r$ from the centre,
$u_{B} = \frac{B^{2}}{2 μ_{0}} = \frac{μ_{0} i^{2}}{8 π^{2} r^{2}}$
Energy in volume of element (length l)
$d U_{B} = u_{B} d V = \frac{μ_{0} i^{2}}{8 π^{2} r^{2}} (2 π r l) d r = \frac{μ_{0} i^{2} l}{4 π} \frac{d r}{r}$
$U_{B} = \frac{μ_{0} i^{2} l}{4 π} \int_{a}^{b} \frac{d r}{r} = \frac{μ_{0} i^{2} l}{4 π} \frac{ln (b)}{a}$
Using values, we get $U = 7 n J$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROMAGNETIC INDUCTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Find the energy stored in the magnetic field if current of 5A produces a magnetic flux of $2 \times 10^{- 3}$ Wb through a coil of 500 turns.
A2.5J
B0.25J
C250J
D1.5J
Question 2 - Select One or More
A coaxial cable consists of a thin inner current carrying conductor fixed along the axis of a hollow current conductor, Let $B_{1}$ and $B_{2}$ be the magnetic fields in the region between the conductors, and outside the conductor respectively.

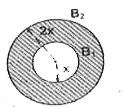A $B_{1} \neq 0, B_{2} \neq 0$ for conductors carrying equal currents in opposite directions
B $B_{1} \neq), B_{2} = 0$ , for conductors carrying equal currents in opposite directions
C $B_{1} \neq 0, B_{2} \neq 0$ , for conductors carrying equal currents in same directions
D $B_{1} = B_{2}$ for conductors carrying equal currents in same directions at distance x and 2x from the axis respectively. 2x gt the radius of the outer cable and x lies between the cables.
Question 3 - Select One
The figure shows the cross-section of a long conducting cylinder of inner radius a and outer radius b. The cylinder carries a current whose current density $J = C r^{2}$ where C is a constant. What is the magnitude of the magnetic field B at a point r, where $a < r < b$ ?

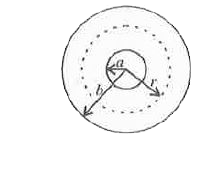A $B = \frac{μ_{0} π C}{4 π r^{2}} (r_{2} - a_{2})$
B $B = \frac{μ_{0} π C}{4 π r^{2}} (r_{4} - a_{4})$
C $B = \frac{μ_{0} π C}{4 π} (r_{2} - a_{2})$
D $B = \frac{μ_{0} π C}{4 π} (r_{4} - a_{4})$

CENGAGE PHYSICS-ELECTROMAGNETIC INDUCTION-Exercises Integer

Home
Ask Doubt
Profile