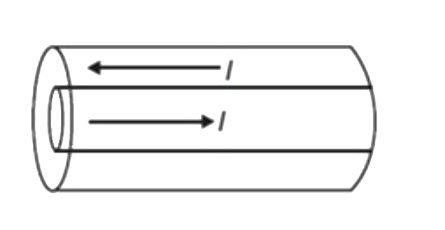
There is one long coaxial cable which consists of two concentric cylinders of radii a and b. Central conductor carries steady current I and outer conductor acts as return path for the current. (i) Calculate energy stored in the magnetic field of length l of such a cable. (ii) Calculate self-inductance for l length of this cable.

Text Solution

Verified by Experts

(i) Magnetic field intensity at a point distance r from the centre of the cable is given by
$B = \frac{μ_{0} I}{2 π r}$
Energy density in terms of distance r can be written as follows:
$u = \frac{B^{2}}{2 μ_{0}}$
$\Rightarrow u = \frac{{(\frac{μ_{0} I}{2 π r})}^{2}}{2 μ_{0}}$
$\Rightarrow u = \frac{μ_{0} I^{2}}{8 π^{2} r^{2}}$

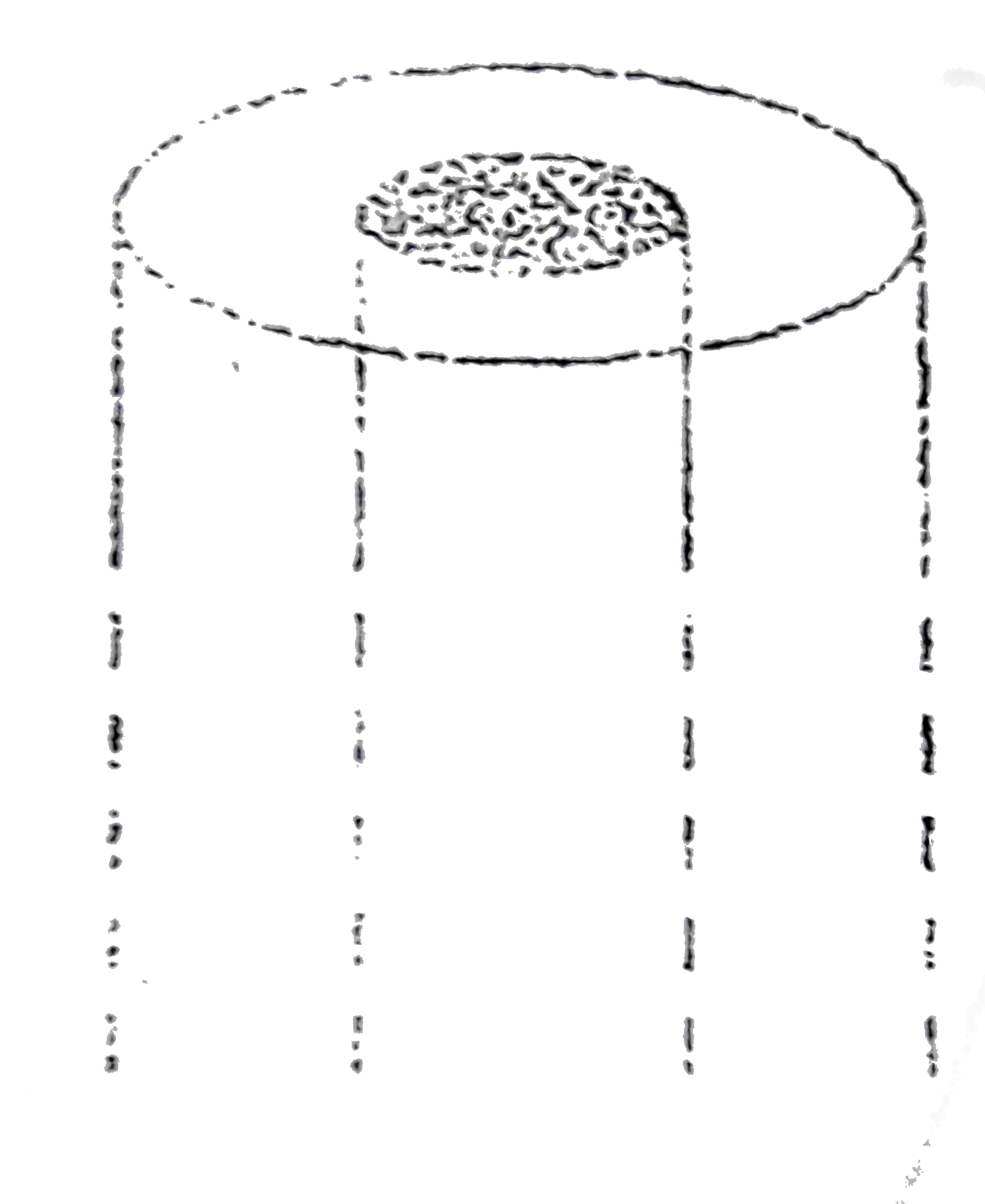
Consider a volume segment dV which is in the form of a cylindrical shell of radii r and r + dr as shown in the figure. Length of this cylindrical shell is l which is perpendicular to the plane shown in figure. Energy density can be assumed to be constant throughout this segment and hence energy stored in this segment can be written as follows:
Energy dU = udV
$d U = \frac{μ_{0} I^{2}}{8 π^{2} r^{2}} 2 π r l d r$
$d U = \frac{μ_{0} I^{2} l}{4 π} \frac{d r}{r}$
Total magnetic energy can be calculated by integrating above relation.
$U = \frac{μ_{0} I^{2} l}{4 π} \int_{a}^{b} \frac{d r}{r}$
$U = \frac{μ_{0} I^{2} l}{4 π} \int_{a}^{b} \frac{d r}{r}$
$U = \frac{μ_{0} I^{2} l}{4 π} In \frac{b}{a}$
(ii) We can use above calculated value of energy stored to calculate self-inductance of this cable. We know that energy stored in an inductor is given as follows:
$U = \frac{1}{2} L I^{2}$
We can equate it with value calculated in part (i)
$\frac{1}{2} L I^{2} = \frac{μ_{0} I^{2} l}{4 π} In \frac{b}{a}$
$L = \frac{μ_{0} l}{2 π} In \frac{b}{a}$

Updated on:21/07/2023