Question

A long cylindrical conductor of radius R carries a current i as shown in the figure. The current density J varies across the cross-section as ${\displaystyle J=k{r}^2}$, where, k is a constant. Find an expression for the magnetic field B at a distance ${\displaystyle r(<R)}$ from the axis

Explanation

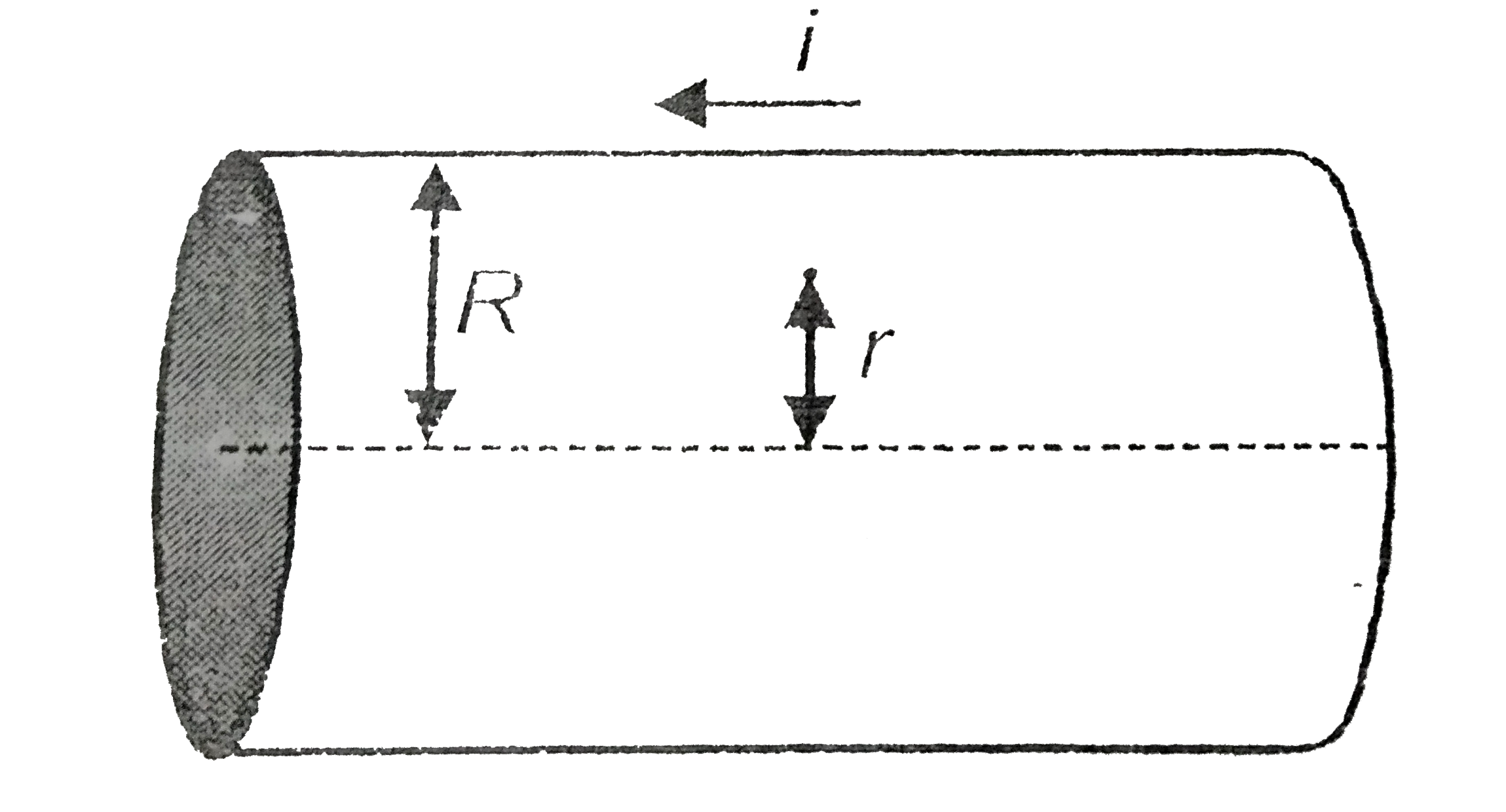
Consider an Amperian loop of radius r as shown. The distribution of current shows that the field will be same everywhere on the Amperian loop
`:. Oint vec(B).vec(dl) = B (2pi r)`
Now `oint vec(B).vec(dl) = mu_(0) i_("enc")` (by Ampere circuital law)
`rArr B = (mu_(0)i_("enc"))/(2pi r)`. To find current enclosed, consider a ring of radius x and thickness dx.

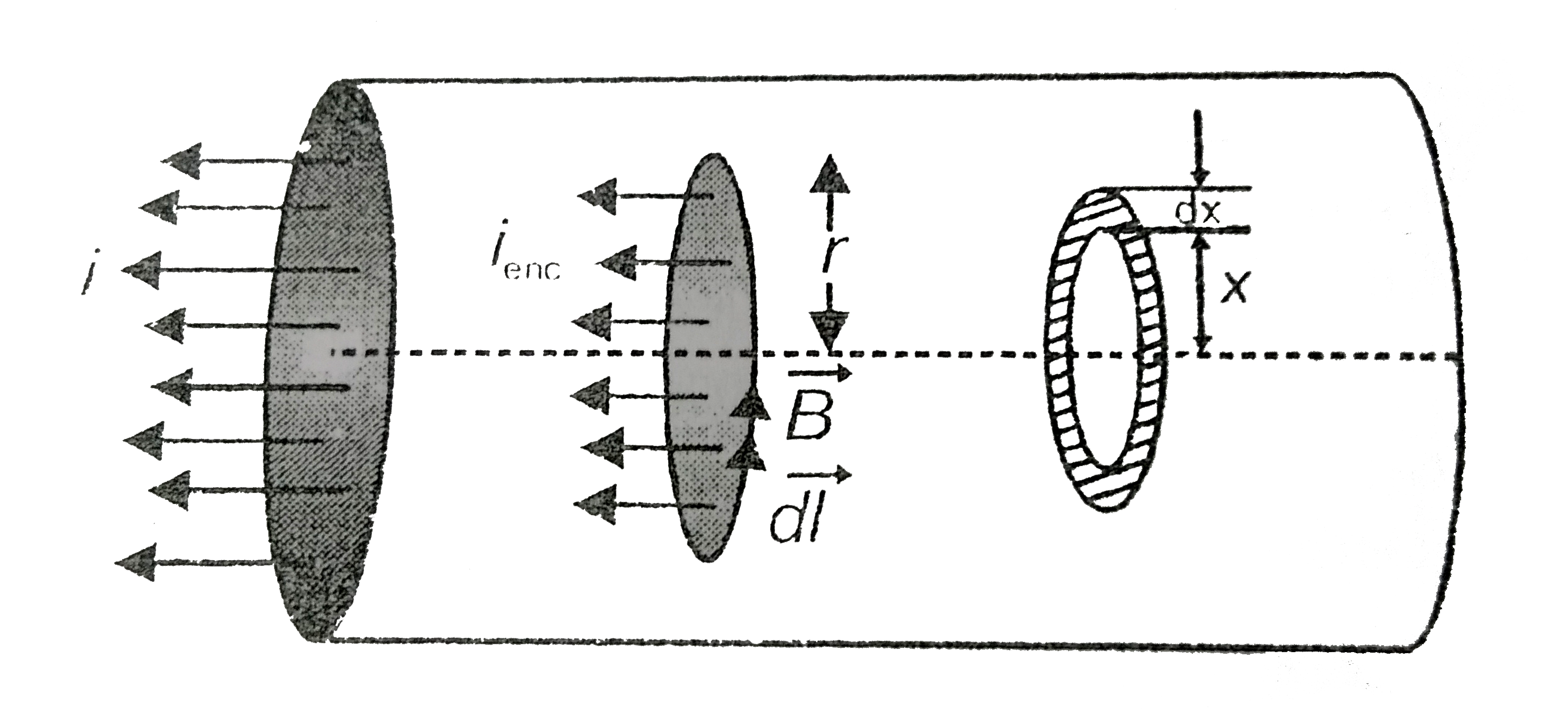
As `i_("enc") = int J xx dA = int_(0)^(r) kx^(2) xx 2pi xx dx`
`rArr i_("enc") = (k xx 2pi r^(4))/(4)`
`rArr B = (mu_(0) kr^(3))/(4)`