A long cylindrical volume contains a uniformly distributed charge of dendity ρ. Find the electric field at a point P inside the cylindrical volume at a distance x from its axis (figure 30-E5) ,
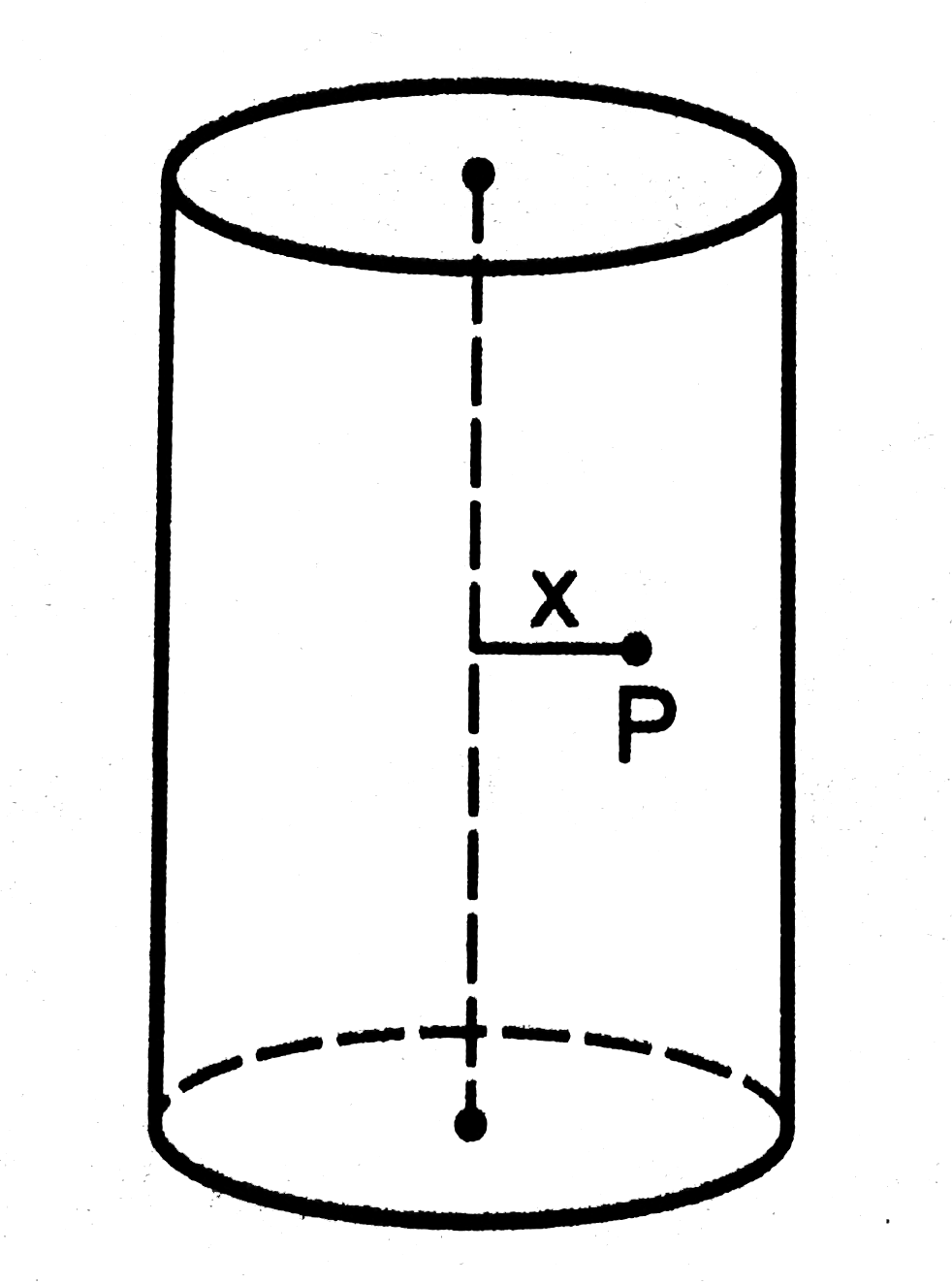
Charge on the cylinder of radius x
=ρπ(x2)h
We know,
∮E.ds=qε0
E.2πxh=(πρ(x2)hε0)<br>orE= rhox / 2 epsilon_0.
Topper's Solved these Questions
Similar Questions
A spherical volume contains a uniformaly distributed charge of density 2.0×104Cm3. Find the electric field at a piont inside the volume at a distance 4.0 cm from the centre.
View SolutionA nonconducting sheet of large surface area and thickness d contains uniform charge distribution of density ρ. Find the electric field at a point P inside the plate, at a distance x from the central plane. Draw a qualitative graph of E against x for 0<x<<d.
View Solution
Knowledge Check
A long cylindrical volume (of radius R) contains a uniformly distributed charge of density ρ. Consider a point P inside the cylindrical volume at a distance x from its axis as shown in the figure. Here x can be more than or less than R. Electric field at point P is :
 Aρx2ε0 if x<RBρxε0 if x<RCρR24ε0x if x>RDρR22ε0x if x>R
Aρx2ε0 if x<RBρxε0 if x<RCρR24ε0x if x>RDρR22ε0x if x>RA ring of radius a contains a charge q distributed uniformly over its length. Find the electric field at a point on the axis of the ring at a distance x from the centre.
Akq2x(a2+x2)32B2kq2x(a2+x2)32Ckq2x(a2+x2)32Dkq22x(a2+x2)32
A long, cylindrical wire of radius b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnetic field at a point inside the wire at a distance a from the axis.
View SolutionA nonconducting sheet of large surface area and thickness d contains uniform charge distribution of density ρ. Find the electric field at a point P inside the plate, at a distance x from the central plane. Draw a qualitative graph of E against x for 0<x<<d.
View SolutionA point charge q is located at the centre fo a thin ring of radius R with uniformly distributed charge −q, find the magnitude of the electric field strength vectro at the point lying on the axis of the ring at a distance x from its centre, if x>>R.
View SolutionElectric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .

View SolutionFigure 22-24 shows a plastic rod having a uniformly distributed charge. The charge per unit length of the rod is λ. Find the electric field due to the rod at a point P which is at a distance r from the rod.
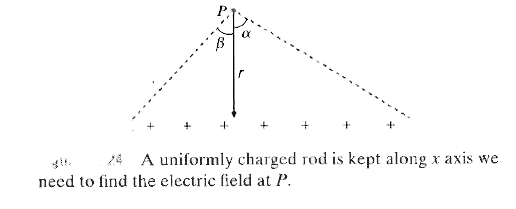
View SolutionA wire of length L carries charge Q uniformly distributed along its length. Find the electric field at a distance √3L2 from the wire at point A as shown.
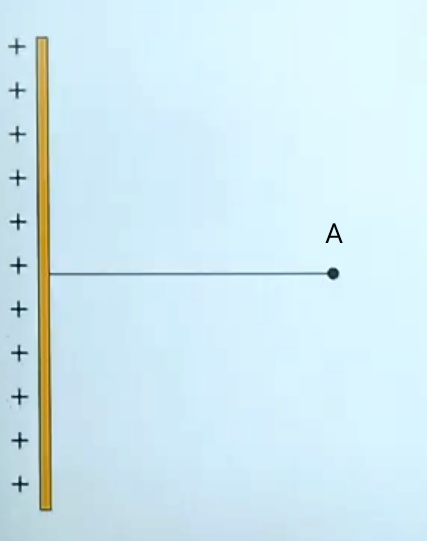
View Solution
