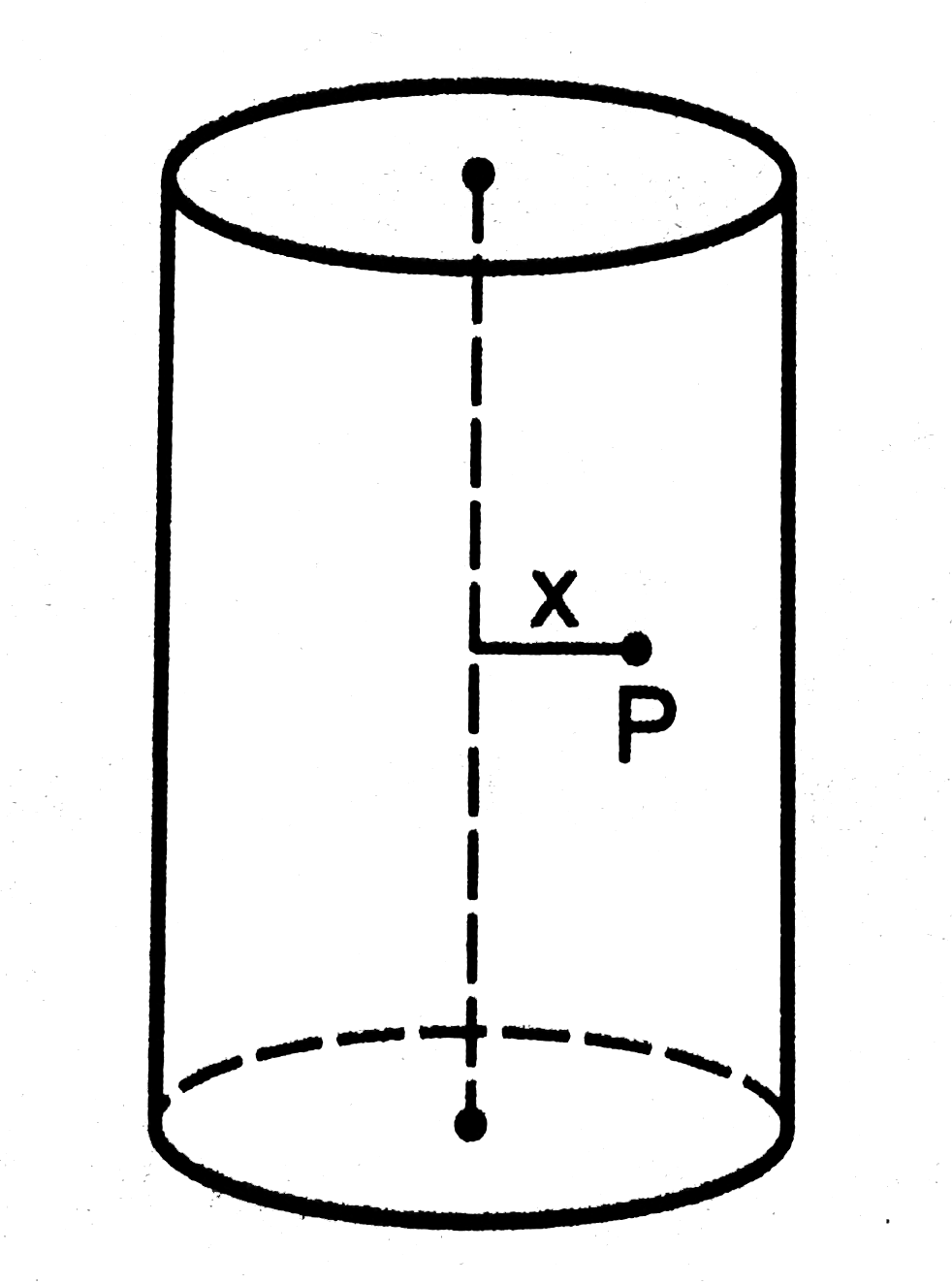
A long cylindrical volume contains a uniformly distributed charge of density ρ. Find the electric field at a point P inside the cylindrical volume at a distance x from its axis (figure 30-E5) ,
 Solution in Tamil
Solution in Tamil
Charge on the cylinder of radius x
=ρπ(x2)h
We know,
∮E.ds=qε0
E.2πxh=(πρ(x2)hε0)<br>orE= rhox / 2 epsilon_0.
Topper's Solved these Questions
Similar Questions
Mark the correct option:
View SolutionShow that the dimensions of the displacement current (ε0dΦEdt) are that of an electric current.
View SolutionA concave mirror having a radius of curvature 40 cm is placed in front of an illuminated point source at a distance of 30 cm from it. Find the location of the image.
View SolutionA ring of radius a contains a charge q distributed uniformly over its length. Find the electric field at a point on the axis of the ring at a distance x from the centre.
View SolutionA long, cylindrical wire of radius b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnetic field at a point inside the wire at a distance a from the axis.
View SolutionFigure shows a uniformly charged hemisphere of radius R. It has a volume charge density rho . If the electric field at a point 2R, above the its center is E, then what is the electric field at the point 2R below its center?
View SolutionFind the electric field due to an infinitely long cylindrical charge distribution of radius R and having linear charge density λ at a distance half of the radius from its axis.
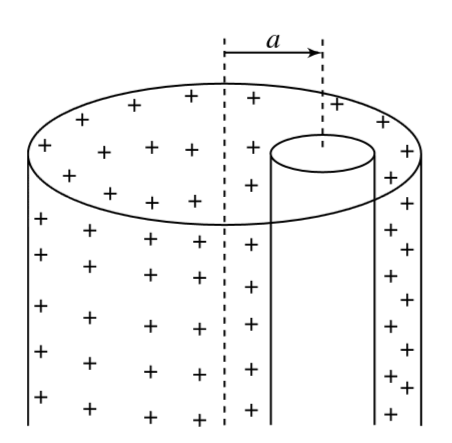
View Solution(a) There is a long uniformly charged cylinder having a volume charge density of ρC/m3. Radius of the cylinder is R. Find the electric field at a point at a distance x from the axis of the cylinder for following cases (i) x lt R (ii) x gt R What is the maximum field produced by the charge distribution at any point? (b) The cylinder described in (a) has a long cylindrical cavity. The axis of cylindrical cavity is at a distance a from the axis of the charged cylinder (see figure). Find electric field inside the cavity.
View SolutionA long cylindrical volume (of radius R) contains a uniformly distributed charge of density rho . Consider a point P inside the cylindrical volume at a distance x from its axis as shown in the figure. Here x can be more than or less than R. Electric field at point P is :
View SolutionA ring of radius a contains a charge q distributed. uniformly ober its length. Find the electric field at a point. on the axis of the ring at a distance x from the centre.
View SolutionA long, cylindrical wire of radius b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnetic field at a point inside the wire at a distance a from the axis.
View SolutionInside an infinitely long circular cylinder charged uniformly with volume density P ther is a circular cylindrical cavity. The distance between the axis of the cylinder and the cavity is equal to a. Find the electric field strenght E inside the cavity. The permittivity us assumed to be equal to unity.
View SolutionThe diagram shows a uniformly charged bemisphere of radius R. It has volume charge density ρ. If the electric field at a point 2R distance below its centre ?
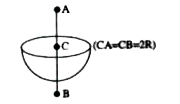
View SolutionFigure shows a uniformly charged hemisphere of radius R. It has a volume charge density rho . If the electric field at a point 2R, above the its center is E, then what is the electric field at the point 2R below its center?
View SolutionAn polaroid long cylindrical object with radius R has a charge distribution that depends upon distance r from the axis like this : ρ=ar+br2(r≤R, a and b are non zero constant, ρ is volume charge density). If electric field outside the cylinder is zero than value of ab is :
View SolutionA long cylindrical volume (of radius R) contains a uniformly distributed charge of density ρ. Consider a point P inside the cylindrical volume at a distance x from its axis as shown in the figure. Here x can be more than or less than R. Electric field at point P is :

View Solution
