A long straight wire of a circular cross-section (radius r) carries a steady current I. The current is distributed uniformly across the cross-section. Calculare the magnetic field at a point (a) outside the wire , (b) inside the wire. Draw a graph showing variation of magnetic field.
(a) Consider a long straight thick wire of a circular cross-section of radius r carrying a steady current I which is distributed uniformly across the cross-section. For a point P1 situated at a normal distance R from central line of wire (where R > r) , consider a circular loop, as shown in fig. as the amperian loop. Then , we have
∮→B.→di=ontBdl−B∮dl−B.2πR=μ0I
⇒B=μ0I2πR
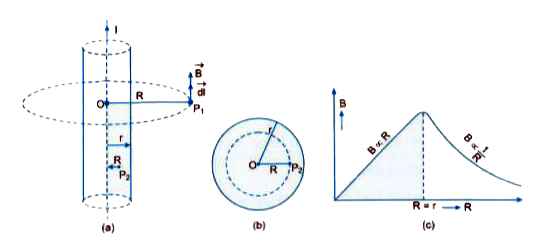
(b) For a point P2 situated at a distance R, where R < r, consider a circular amperian loop as shown in fig. Then
∮→B.→dl=∮Bdl=B∮dl=B.2πR
But now the current enclosed is only Ie=I(πR2πr2)=IR2r2. Hence, as per Ampere.s circuital law :
B.2πr=μ0Ie=μ0IR2r2⇒B=μ0IR2πr2
Moreover field at the surface of wire (R=r) will be B=μ0I2πr, which is maximum, Variation of magnetic field B with distance R from the axis of thick wire is shown in fig.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISM BOOK - U-LIKE SERIESCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - LONG ANSWER QUESTIONS-II
11 Videos
- MOVING CHARGES AND MAGNETISM BOOK - U-LIKE SERIESCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - SELF ASSESSMENT TEST (SECTION A) (MULTIPLE CHOICE QUESTIONS)
5 Videos
- MOVING CHARGES AND MAGNETISM BOOK - U-LIKE SERIESCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - SHORT ANSWER QUESTIONS
41 Videos
- MODEL TEST PAPER 3 (UNSOLVED)BOOK - U-LIKE SERIESCHAPTER - MODEL TEST PAPER 3 (UNSOLVED)EXERCISE - SECTION A
3 Videos
- NUCLEIBOOK - U-LIKE SERIESCHAPTER - NUCLEIEXERCISE - Self Assessment Test
10 Videos
Similar Questions
Figure shows a long straight wire of circular crosssection (radius a) carrying steady current I. The current I is uniformly distributed across this crosssection. Calculate the magnetic field in the region r<a and r>a.

View SolutionFigure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region r<aandr>a

View Solution
Knowledge Check
A long straight wire of radius a carries a steady current i. The current is uniformly distributed across its cross section. The ratio of the magnetis field at (a)/(2)and(2a) is
A(1/2)B(1/4)C4D1
Figure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region r<aandr>a

View SolutionFigure shows a long straight wire of circular crosssection (radius a) carrying steady current I. The current I is uniformly distributed across this crosssection. Calculate the magnetic field in the region r<a and r>a.

View SolutionFigure shows a long straight wire of circular crosssection (radius a) carrying steady current I. The current I is uniformly distributed across this crosssection. Calculate the magnetic field in the region r<a and r>a.

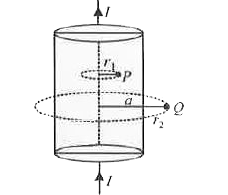
View SolutionFigure show a long straight wire of a circular a cross-section with radius 'a' carrying steady curent I. The curent I is uniformaly distributed across this c ross -section.Calclulate the magnetic field in the regionr1<aandr2> a.
View SolutionFigure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region r<aandr>a

View SolutionA long straight wire of a circular cross section (radius a) carrying steady current. Current is uniformly distributed in the wire. Calculate magnetic field inside the region (r<a) in the wire.
View SolutionA long straight wire of a circular cross-section of radius 'a' carries a steady current I. The current is uniformly distributed across the cross-section. Apply Ampere's circuital law to calculate the magnetic field at a point at distance 'r' in the region for (i) r<a and (ii) r>a.
View Solution
