A long thin solenoid has 900tuns/metre and radius 2.50cm,. The current in the solenoid is increasing at a uniform rate of 60A/s. What is the magnitude of the induced electric field at a point?
a. 0.5cm from the axis of the solenoid.
b. 1.0cm from the axis of the solenoid.
To solve the problem, we need to find the induced electric field at two different points from the axis of a solenoid with given parameters. Let's break down the solution step by step.
Given Data:
- Number of turns per meter (n) = 900 turns/m
- Radius of the solenoid (R) = 2.50 cm = 0.025 m
- Rate of change of current (di/dt) = 60 A/s
- Permeability of free space (μ₀) = 4π × 10^(-7) T·m/A
Step 1: Calculate the rate of change of magnetic field (dB/dt)
The magnetic field inside a long solenoid is given by the formula:
B=μ0nI
Where I is the current flowing through the solenoid. Since the current is changing, we differentiate with respect to time:
dBdt=μ0ndidt
Substituting the values:
dBdt=(4π×10−7T⋅m/A)×(900turns/m)×(60A/s)
Calculating this:
dBdt=4π×10−7×900×60
dBdt≈0.068T/s
Step 2: Calculate the induced electric field (E) at a distance r from the axis
The induced electric field at a distance r from the axis of the solenoid can be calculated using the formula:
E=r2dBdt
Step 3: Calculate E at 0.5 cm (0.005 m) from the axis
Substituting r=0.005m:
E0.5=0.0052×0.068
E0.5=0.0025×0.068
E0.5≈1.7×10−4V/m
Step 4: Calculate E at 1.0 cm (0.01 m) from the axis
Substituting r=0.01m:
E1.0=0.012×0.068
E1.0=0.005×0.068
E1.0≈3.4×10−4V/m
Final Results:
- Induced electric field at 0.5 cm from the axis: E0.5≈1.7×10−4V/m
- Induced electric field at 1.0 cm from the axis: E1.0≈3.4×10−4V/m
- Number of turns per meter (n) = 900 turns/m
- Radius of the solenoid (R) = 2.50 cm = 0.025 m
- Rate of change of current (di/dt) = 60 A/s
- Permeability of free space (μ₀) = 4π × 10^(-7) T·m/A
The magnetic field inside a long solenoid is given by the formula:
B=μ0nI
Where I is the current flowing through the solenoid. Since the current is changing, we differentiate with respect to time:
dBdt=μ0ndidt
dBdt=(4π×10−7T⋅m/A)×(900turns/m)×(60A/s)
dBdt=4π×10−7×900×60
dBdt≈0.068T/s
The induced electric field at a distance r from the axis of the solenoid can be calculated using the formula:
E=r2dBdt
Substituting r=0.005m:
E0.5=0.0052×0.068
E0.5=0.0025×0.068
E0.5≈1.7×10−4V/m
Substituting r=0.01m:
E1.0=0.012×0.068
E1.0=0.005×0.068
E1.0≈3.4×10−4V/m
- Induced electric field at 0.5 cm from the axis: E0.5≈1.7×10−4V/m
- Induced electric field at 1.0 cm from the axis: E1.0≈3.4×10−4V/m
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Check point
60 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Taking it together
119 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 2 Subjective
20 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
A 0.8 m long solenoid has 800 turns and a field density of 2.52×10−3 T at its certre .Find the current in the solenoid
View SolutionA solenoid of length 8cm has 500 turns /m in it. If radius of coil is 3cm and if it is carrying a current of 2A, find the magnetic induction at a point 4cm from the end on the axis of the solenoid
View SolutionA solenoid of length 0⋅5m has a radius of 1cm and is made up of 500 turns. It carries a current of 5A. What is the magnitude of the magnetic field inside the solenoid?
View SolutionA long solenoid with radius 2cm carries a current of 2A. The solenoid is 70cm long and is composed of 300 turns of wire. Assuming ideal solenoid model, calculate the flux linked with a circular surface if
(a) it has a radius of 1cm and is perpendicular to the axis of the solenoid:
(i) inside,
(ii) outside.
(b)it has a radius of 3cm and is perpendicular to the axis of the solenoid with its center lying on the axis of the solenoid.
( c ) it has a radius greater than 2cm and axis of the solenoid subtend an angle of 60∘ with the normal to the area (the center of the circular surface being on the axis of the solenoid).
(d) the plane of the circular area is parallel to the axis of the solenoid.
View SolutionA solenoid consists of 100 turns of wire and has a length of 10 cm. The magnetic field inside the solenoid when it carries a current of 0.5 A will be :
View SolutionA solenoid of radius 2.50cm has 400turns and a length of 20.0cm. The current in the coil is changing with time such that an emf of 75X10^(-6) is produced.
The rate of change of current in the solenoid is
View SolutionThe magnetic field at a point on the axis of a long solenoid having 5 turns per cm length when a current of 0.8 A flows through it is
View SolutionIf the current in the toroidal solenoid increases uniformly from zero to 6.0 A in 3.0μs Self-inductance of the toroidal solenoid is 40μ H The magnitude of self-induced emf is
View SolutionA long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.
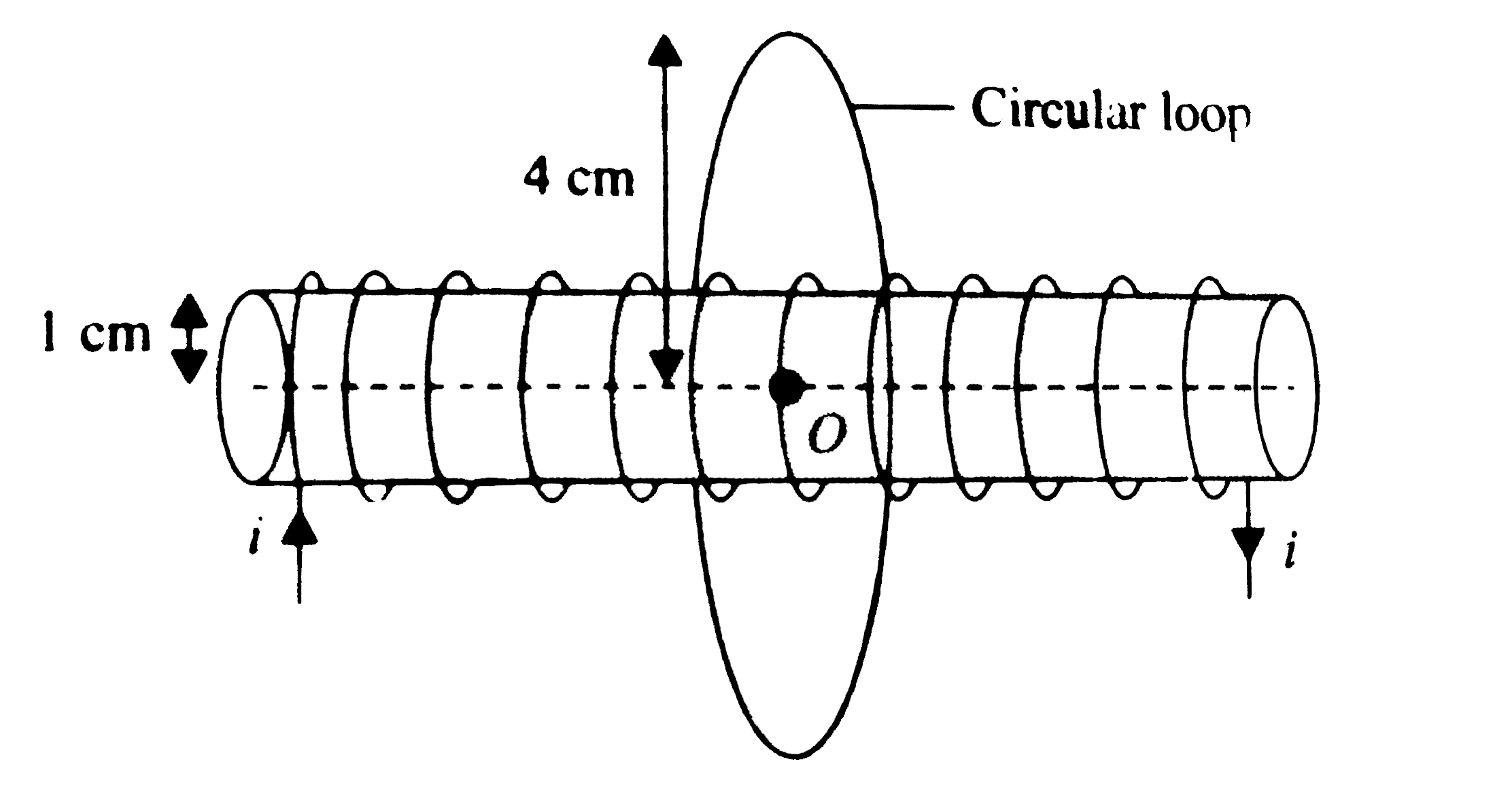
A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
Magentic flux through the loop due to external magnetic field will be
I is the current in the loop
a1 is the radius of solendoid and a1=1cm (given)
a2 is the radius of circular loop and a2=4cm (given)
i is hte current in the solenoid
View SolutionA long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.

A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
When the current in the solenoid becomes zero so that external magnetic field for the loop stops changing, current in the loop will follow a differenctial equation given by [You may use an approximation that field at all points in the area of loop is the same as at the centre
View Solution
