A loop of mass M and radius R is rolling on a smooth horizontal surface with speed 'v'. It's total kinetic energy is
1/2Mv2
3/2Mv2
Mv2
1/2MR2ω2
The correct Answer is:C
To find the total kinetic energy of a loop of mass M and radius R rolling on a smooth horizontal surface with speed v, we need to consider both the translational and rotational kinetic energies.
1. Identify the Components of Kinetic Energy:
- The total kinetic energy (KEtotal) of the loop consists of two parts: translational kinetic energy (KEtrans) and rotational kinetic energy (KErot).
KEtotal=KEtrans+KErot
2. Calculate Translational Kinetic Energy:
- The translational kinetic energy of the loop is given by the formula:
KEtrans=12Mv2
3. Calculate Rotational Kinetic Energy:
- The rotational kinetic energy is given by the formula:
KErot=12Iω2
- For a loop, the moment of inertia I about its center of mass is:
I=MR2
- The angular velocity ω can be related to the linear speed v by the equation:
ω=vR
- Substituting ω into the rotational kinetic energy formula:
KErot=12(MR2)(vR)2=12MR2⋅v2R2=12Mv2
4. Combine Both Kinetic Energies:
- Now, we can combine both kinetic energies to find the total kinetic energy:
KEtotal=KEtrans+KErot=12Mv2+12Mv2=Mv2
Final Answer:
The total kinetic energy of the loop is:
KEtotal=Mv2
- The total kinetic energy (KEtotal) of the loop consists of two parts: translational kinetic energy (KEtrans) and rotational kinetic energy (KErot).
KEtotal=KEtrans+KErot
- The translational kinetic energy of the loop is given by the formula:
KEtrans=12Mv2
- The rotational kinetic energy is given by the formula:
KErot=12Iω2
- For a loop, the moment of inertia I about its center of mass is:
I=MR2
- The angular velocity ω can be related to the linear speed v by the equation:
ω=vR
- Substituting ω into the rotational kinetic energy formula:
KErot=12(MR2)(vR)2=12MR2⋅v2R2=12Mv2
- Now, we can combine both kinetic energies to find the total kinetic energy:
KEtotal=KEtrans+KErot=12Mv2+12Mv2=Mv2
The total kinetic energy of the loop is:
KEtotal=Mv2
Topper's Solved these Questions
Similar Questions
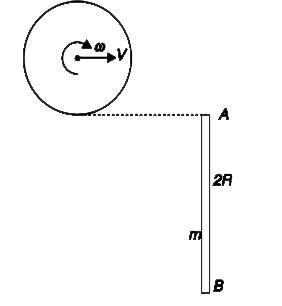
A disc of mass m and radius R is moving on a smooth horizontal surface with the flat circular face on the surface. It is spinning about its centre with angular peed ω and has a velocity V (see figure). It just manages to hit a stick AB at its end A. The stick was lying free on the surface and stick to the disc. [The combined object becomes like a badminton racket]. Mass and length of the stick are m and 2R respectively.
(a) Calculate the angular speed of the combined object assuming V=Rω
(b) Calculate loss in kinetic energy. Why is energy lost ?
(c) If V=η(Rω), loss in kinetic energy is minimum. Find η. (Assume ω is given]
View SolutionA sphere of mass m and radius r rolls without slipping on the horizontal surface with speed v. During its motion it encounters a fixed rectangular block of height h=r4 as shown. The collision is inelastic. Find the angular speed of sphere immediately after collision. The body rolls without slipping.
View Solution
Knowledge Check
A solid cylinder of mass 1 kg and radius 0.02 m, is rolling on a smooth horizontal surface with a uniform velocity of 0.1 m/s. Its total energy is
A7.5×10−3JB7.5×10−2JC7.5×10−4JD7.5×10−6JA solid sphere of mass 10 kg and diameter 5 cm rolls without slipping on a smooth horizontal surface with velocity 5 cm/s. Its total kinetic energy is
A175×10−4JB175×10−3JC175×10−5JD175×10−6JIf a disc of mass 400 gm is rolling on a horizontal surface with uniform speed of 2 m/s, then its rolling kinetic energy will be
A0.12 JB1.2 JC120 JD12 J
A symmetrical body of mass M and radius R is rolling without slipping on a horizontal surface with linear speed v. Then its angular speed is
View SolutionA 1.0 kg wheel in the form of a solid disk rolls along a horizontal surface with a speed of 6.0 m/s. What is the total kinetic energy of the wheel?
View SolutionA solid sphere of radius r r is rolling on a horizontal surface. The ratio between the rotational kinetic energy and total energy.
View SolutionA solid sphere of mass M and radius R is placed on a smooth horizontal surface. It is given a horizontal impulse J at a height h above the centre of mass and sphere starts rolling then, the value of h and speed of centre of mass are –
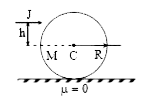
View SolutionA uniform solid sphere of mass M and radius R is placed on a smooth horizontal surface. It is given a horizontal impulse J at a height h above the centre of mass and sphere starts rolling. Then the value of h and speed of ccentre of mass are
View Solution
