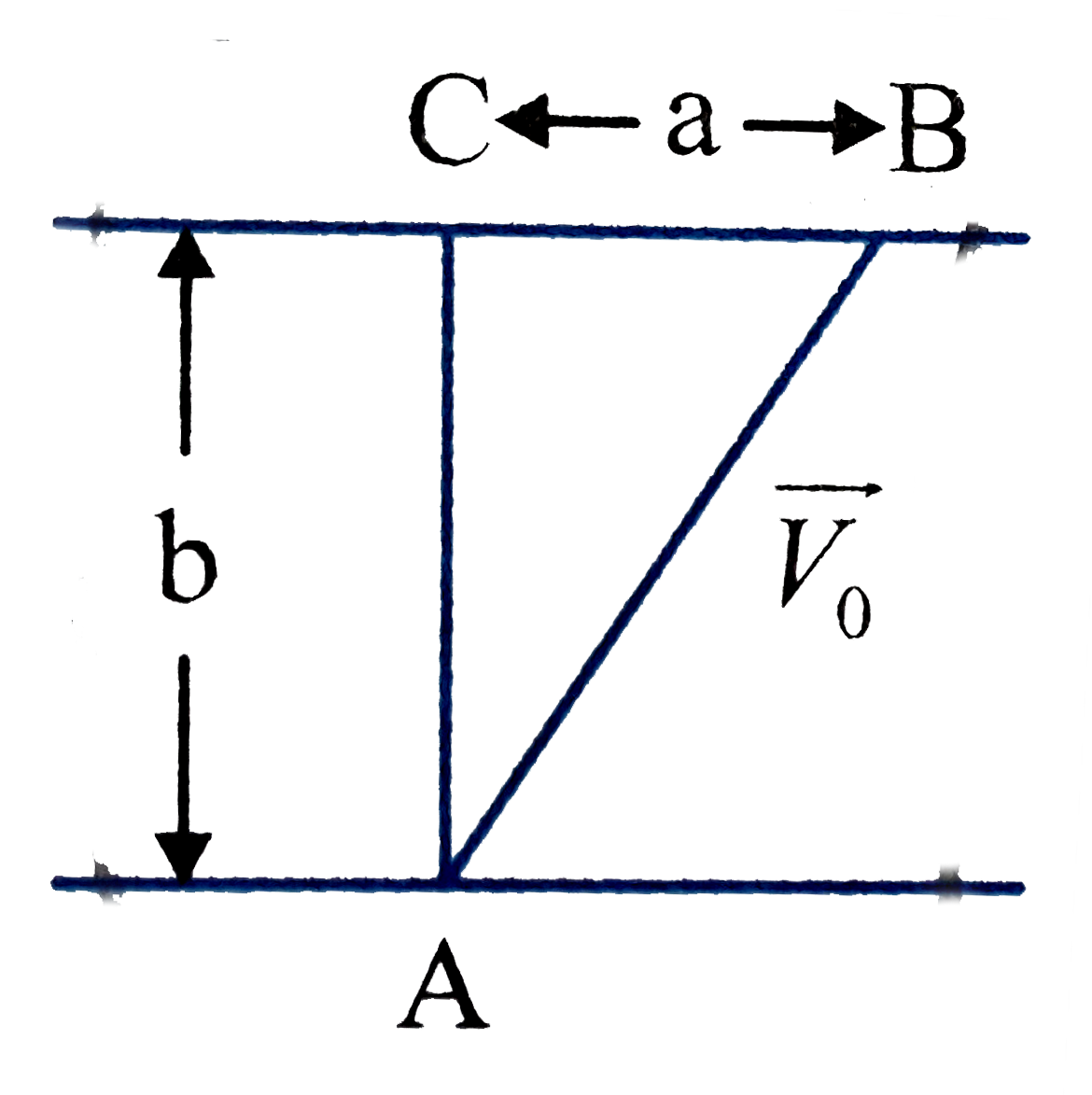
A man in a river boat must get from point A to point B on the opposite bank of the river (see figure).The distance BC=a.The width of the river AC=b.At what minimum speed u relative to the still water should the boat travel to reach the point B?The velocity of flow of the river is v0
v0b√a2+b2
v0a√a2+b2
v0b√2a
v0a√2b
The correct Answer is:a
Suppose u is the speed of the boat relative to water, then velocity of the flow (w.r.t. bank) v0.
vx=(ucosθ+v0), and perpendicu lar to flow will be uy=usinθ
Time to cross the river, t=businθ In the time, the distance travelled by the boat in the direction of flow.
a=vxt=(ucosθ+v0)businθ
or ausinθ=ubcosθ+v0b
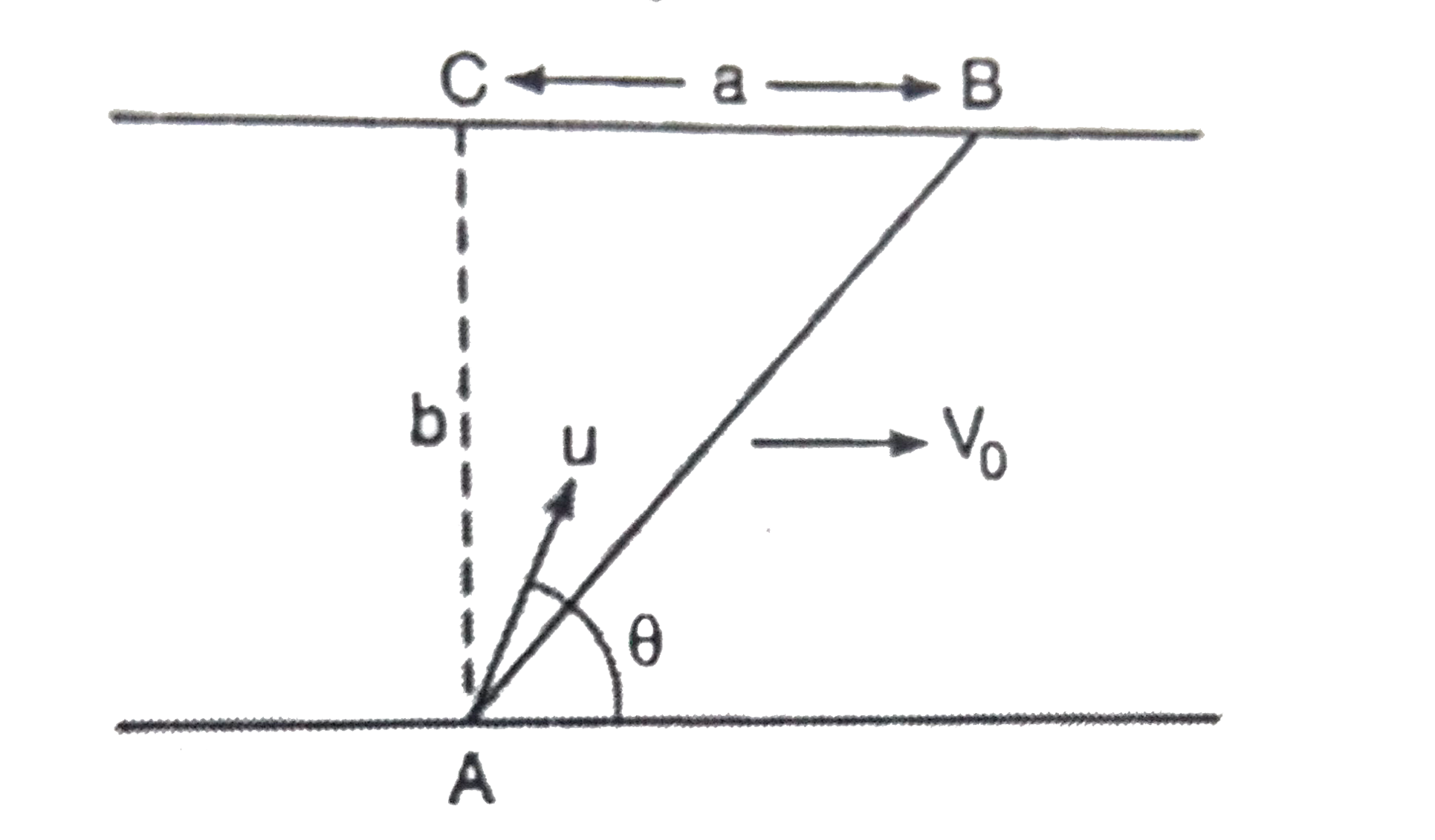
∴u=v0b(αsinθ−bcosθ).............(i) u to be minimum.
θ=0 or ddthη[v0bαsinθ−bcosθ]=0
or tanθ=−ab∴cosθ=b√a2+b2
On substituting these values in equation (i), we get
umin=v0b√a2+b2
Topper's Solved these Questions
Similar Questions
A man wants to reach point B on the opposite bank of a river flowing at a speed u as shown in (Fig. 5.193). What minimum speed relative to water to water should the man have so that he can reach directly to point B ? In which direction should he swim ?
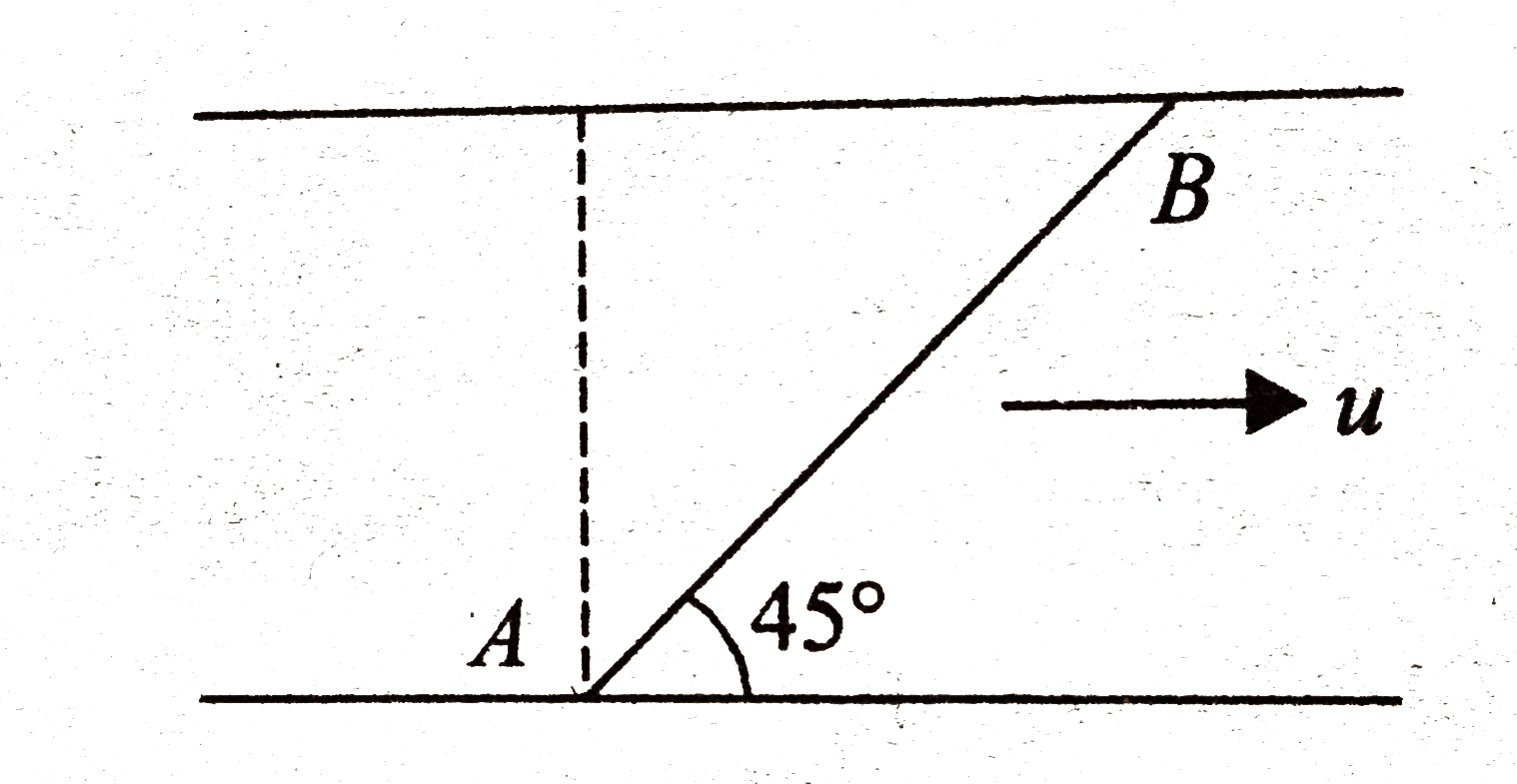 .
.
View SolutionA man wants to reach point B on the opposite bank of a river flowing at a speed as shown in figure. What minimum speed relative to water should the man have so that he can reach point B? In which direction should he swim?
View Solution
Knowledge Check
A man in a row boat must get from point A to point B on the opposite bank of the river (see figure).The distance BC=a.The width of the river AC=b.At what minimum speed u relative to the still water should the boat travel to reach the point B?The velocity of flow of the river is v0
 Av0b√a2+b2Bv0a√a2+b2Cv0b√2aDv0a√2b
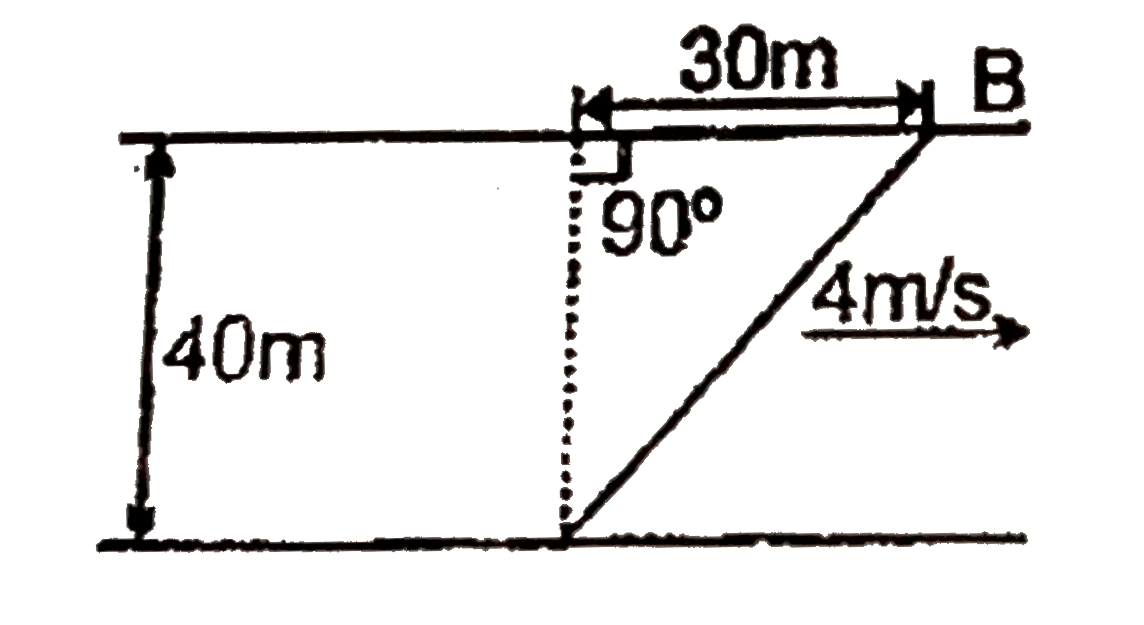
Av0b√a2+b2Bv0a√a2+b2Cv0b√2aDv0a√2bA man wants to reach point B on the opposite bank of a river flowing at a speed 4m/s as shown in the figure. What minimum speed relative to water should the man have so that he can reach point B directly by swimming?
 A8m/sB3.2m/sC6.5m/sD7√2m/s
A8m/sB3.2m/sC6.5m/sD7√2m/sA man who can swim at a speed v relative to the water wants to cross a river of width d, flowing with a speed u. The point opposite him across the river is P.
AThe minimum time in which he can cross the river is dvBHe can reach the point P in time dvCHe can reach the point P in time d√v2−u2DHe cannot reach P if u>v
A man wants to reach point B on the opposite bank of a river flowing at a speed 4m/s as shown in the fig 1E.125 (a) what minimum speed relative to water should the man have so that he can reach point B directly by swimming? In which direction should he swin?
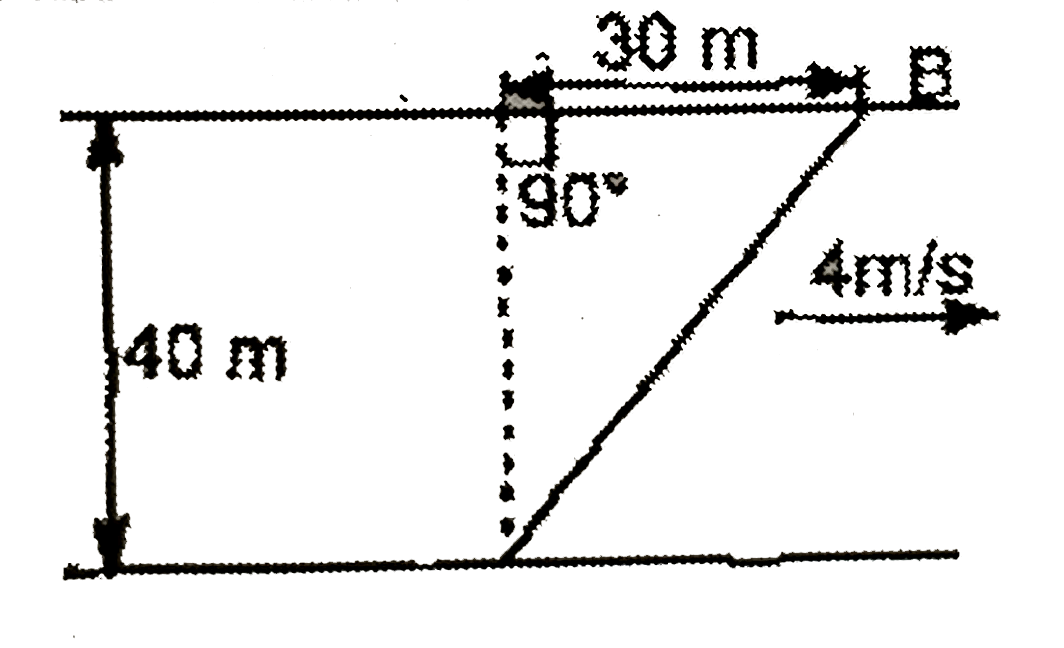
View SolutionThe velocity of water current in a river changes with distance along the perpendicular to the river according to the law u=2u0dy for 0≤y≤d2 where u0= velocity in the mid-stream d= width of the river =2u0d(d−y) for d2≤y≤d.
A boat travels from a point O on one block of the river to the opposite bank and its steering angle is constantly changed to keep its relative velocity perpendicular to the river current. Calculate the time in which the boat will reach the other bank. The velocity of the boat in still water is u0.
View SolutionA swimmer starts to swim from point a to cross a river. He wants to reach point B on the opposite side of the river. The line AB makes an angle 60∘ with the river flow as hown. The velocity of the swimmer in still water is same as that of the water

(i) In what direction should he try to direct his velocity ? Calculate angle between his velocity anf river velocity.
(ii) Find the ratio of the time taken to cross the river in this situation to the minimum time in which he can cross this river.
View SolutionA man who can swim at a speed v relative to the water wants to cross a river of width d flowing with a speed u. The point opposite him across the river is A.
View SolutionA boat takes 10 minutes to cross a river in a straight line from a point A on the bank to a point B on the other bank and 20 minutes to do the return journey. The current flows at 3 km/h. and the speed of the boat relative to water is 6 km/h. The width of the river and the down stream distance from A to B are
View Solution
