A man places a chain (of mass m and length l) on a table slowly. Initially, the lower end of the chain just touches the table. The main brings down the chain by length l/2. Work done by the man in this process is
(a) −mg12
(b) −mgl4
(c) −3mgl8
(d) −mgl8
The correct Answer is:C
To solve the problem, we need to calculate the work done by the man while lowering the chain by a length of l2. The work done can be determined by calculating the change in potential energy of the chain.
1. Understanding the Initial Position of the Chain:
- Initially, the lower end of the chain just touches the table, and the entire chain is hanging vertically. The center of mass of the chain is at a height of l2 from the table.
2. Calculating Initial Potential Energy (PE_initial):
- The potential energy of the chain can be calculated using the formula:
PEinitial=mgh
- Here, h=l2 (the height of the center of mass), so:
PEinitial=mg(l2)=mgl2
3. Understanding the Final Position of the Chain:
- After lowering the chain by l2, half of the chain (length l2) is on the table, and the other half is still hanging.
- The center of mass of the hanging part (which is now l2) is at a height of l4 from the table.
4. Calculating Final Potential Energy (PE_final):
- The mass of the hanging part is m2 (since half of the chain is hanging). The potential energy of this hanging part is:
PEfinal=(m2)g(l4)=mgl8
5. Calculating the Change in Potential Energy:
- The work done by the man is equal to the change in potential energy:
ΔPE=PEfinal−PEinitial
- Substituting the values:
ΔPE=mgl8−mgl2
- To combine these, convert mgl2 to a fraction with a denominator of 8:
mgl2=4mgl8
- Now substituting:
ΔPE=mgl8−4mgl8=−3mgl8
6. Conclusion:
- The work done by the man in lowering the chain is:
W=−3mgl8
- The negative sign indicates that the work is done against the gravitational force.
Final Answer:
The work done by the man in this process is −3mgl8.
- Initially, the lower end of the chain just touches the table, and the entire chain is hanging vertically. The center of mass of the chain is at a height of l2 from the table.
- The potential energy of the chain can be calculated using the formula:
PEinitial=mgh
- Here, h=l2 (the height of the center of mass), so:
PEinitial=mg(l2)=mgl2
- After lowering the chain by l2, half of the chain (length l2) is on the table, and the other half is still hanging.
- The center of mass of the hanging part (which is now l2) is at a height of l4 from the table.
- The mass of the hanging part is m2 (since half of the chain is hanging). The potential energy of this hanging part is:
PEfinal=(m2)g(l4)=mgl8
- The work done by the man is equal to the change in potential energy:
ΔPE=PEfinal−PEinitial
- Substituting the values:
ΔPE=mgl8−mgl2
- To combine these, convert mgl2 to a fraction with a denominator of 8:
mgl2=4mgl8
- Now substituting:
ΔPE=mgl8−4mgl8=−3mgl8
- The work done by the man in lowering the chain is:
W=−3mgl8
- The negative sign indicates that the work is done against the gravitational force.
The work done by the man in this process is −3mgl8.
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Linked Comprehension
55 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Subjective
23 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
What will be the work done by external agent to slowly hang the lower end of the chain to the peg?
View SolutionA uniform chain of mass m and length l overhangs a table with its two third part on the table. Fine the work to be done by a person to put the hanging part back on the table.
View SolutionA uniform chain of mass m and length l is lying on a horizontal table with one-third of its length hanging over the edge of the table.

What is the speed of the chain, when it just loses contact with the table?
View SolutionHalf length of the chain of mass m and length / is overhanging. What is speed of chain when it just slips off the smooth table?
View SolutionA chain of mass m and length l lies on a horizontal table. The chain is allowed to slide down gently from the side of the table. Find the speed of the chain at the instant when last link of the chain slides from the table. Neglect friction everywhere.
(a) the force from thelicopter and
(b) the gravitational force on her
(c ) What are speed ot the kinetic energy and.
(d) the speed of the astronaut just before she reaches the helicopter?
View SolutionA uniform chain of mass m & length L is kept on a smooth horizontal table such that Lnportion of the chaing hangs from the table. The work dione required to slowly bringsthe chain completely on the table is
View SolutionA very flexible uniform chain of mass M and length L is suspended vertically so that its lower and just touches the surface of a table. When the upper end of the chain is released it falls with each link coming to rest the instant it strikes the table. Find the force exerted by the chain on the table at the moment when y part of the chain has already rested on the table.
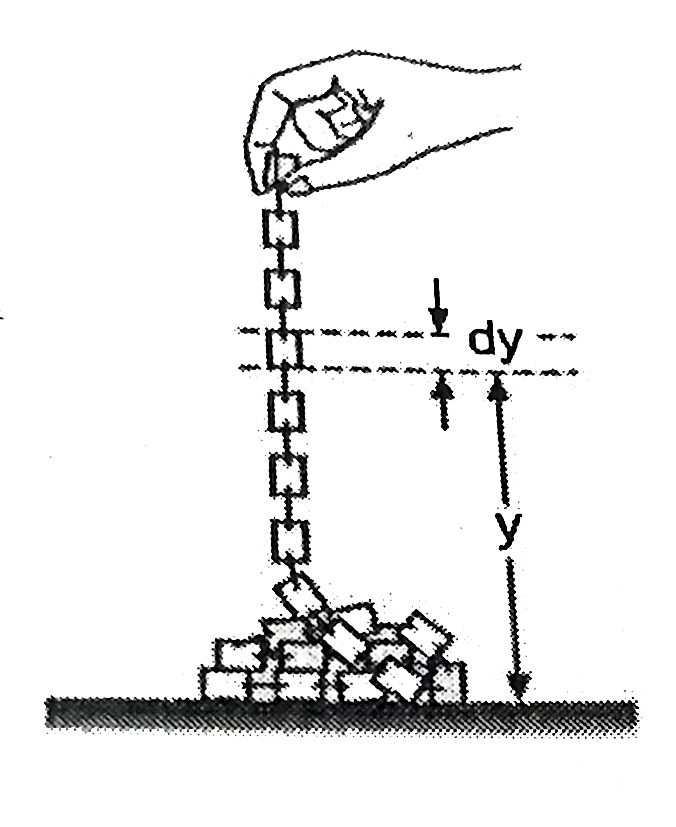
View SolutionA uniform rope of mass m per unit length, hangs vertically from a support so that the lower end just touches the table top shown in figure. If it is released, show that at the time a length y of the rope has fallen, the force on the table is equivalent to the weight of the length 3y of the rope.

View SolutionA uniform chain of mass m and length l is at the verge of sliding under the effect of gravity of the hanging part. Find the

a. coefficient of friction, between chain and table.
b. work done by friction and gravity till the chain leaves the table if the hanging part is pulled gently and released.
c. speed of the chain at the time of leaving the table in part (b) .
d. work done by the external force acting at the end A of the chain in slowly pulling the chain completely onto the table.
View SolutionA uniform chain of length L and mass M overhangs a horizontal table with its two third part on the table. The friction coefficient between the table and the chain is µ. The work done by the friction during the period the chain slips off the table is [−2kμMgL]. Find the value of k.
View Solution
