Question

A mass $m$ is placed at $P$ a distance $h$ along the normal through the centre $O$ of a thin circular ring of mass $M$ and radius $r$ Fig.
If the mass is removed futher away such that $OP$ becomes $2h$, by what factor the force of gravitational will decrease, if $h=r$ ?

Explanation

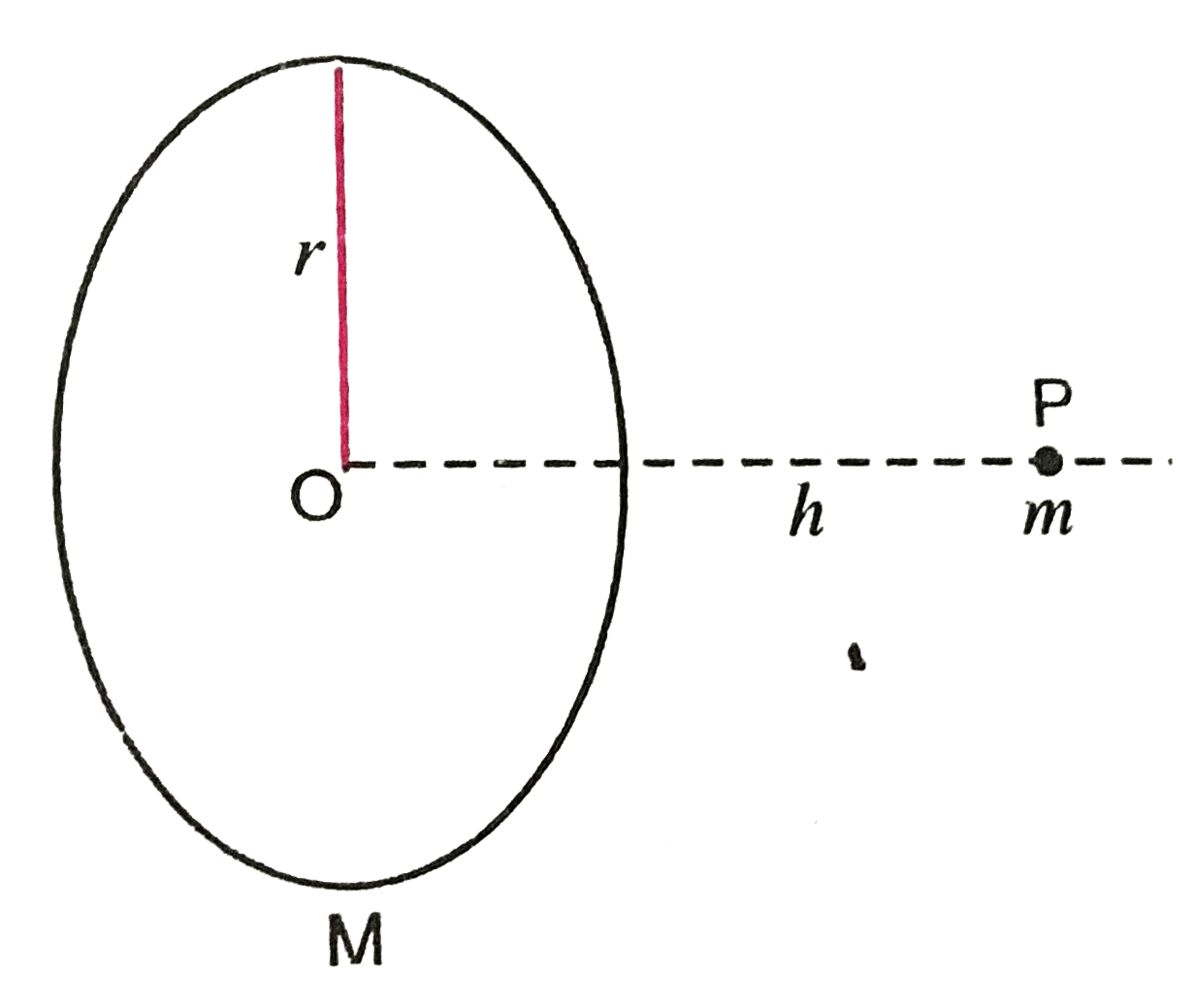
Consider the diagram, in which a system consisting of a ring and a point mass is shown

Gravitational force acting on an object of mass m, placed at point P at a distance `h` along the normal through the centre of a circular ring of mass M and radius `r` is given by
`F = (GMmh)/((r^(2) + h^(2))^(3//2))`(along PO)....(i)
When mass is displaced upto distance `2h`, then
`F' = (GMm xx 2h)/([r^(2) + (2h)^(2)]^(3//2)) " " [:. h = 2r]`
When `h = r`, then from Eq. (i)
`F = (GMm xx r)/((r^(2) + r^(2))^(3//2)) rArr F = (GMm)/(2sqrt(2r^(2)))`
and `F' (2GMmr)/((r^(2) + 4r^(2))^(3//2)) = (2GMm)/(5 sqrt(5r^(2)))` [From Eq. (ii) substituting `h = r`]
`:. (F')/(F) = (4sqrt2)/(5sqrt5)`
`rArr F' = (4sqrt2)/(5sqrt5) F`