A mass of 6 kg is suspended by a rope of length 2 m from the ceilling A force of 50 N in the horizontal direction is applied at the mid - point P of the rope as shown . What is the angle the rope makes with the vertical in equilibrium ? (Take = 10ms−2) . Neglect mass of the rope .
To solve the problem of finding the angle the rope makes with the vertical in equilibrium when a horizontal force is applied, we can follow these steps:
Step 1: Identify the forces acting on the mass
The forces acting on the mass are:
1. The weight of the mass (W) acting downwards, which is given by:
W=mg
where m=6kg and g=10m/s2.
2. The tension (T) in the rope acting at an angle θ with the vertical.
3. The horizontal force (F) of 50 N acting at the midpoint of the rope.
Step 2: Calculate the weight of the mass
Substituting the values into the weight formula:
W=mg=6kg×10m/s2=60N
Step 3: Set up the equilibrium conditions
In equilibrium, the vertical and horizontal components of the forces must balance out.
- Vertical forces:
The vertical component of the tension must balance the weight of the mass:
Tcos(θ)=W
Substituting the weight:
Tcos(θ)=60N(1)
- Horizontal forces:
The horizontal component of the tension must balance the applied horizontal force:
Tsin(θ)=F
Substituting the horizontal force:
Tsin(θ)=50N(2)
Step 4: Divide the equations to eliminate T
Dividing equation (2) by equation (1):
Tsin(θ)Tcos(θ)=5060
This simplifies to:
tan(θ)=5060=56
Step 5: Calculate the angle θ
To find θ, take the arctangent:
θ=tan−1(56)
Using a calculator or trigonometric tables:
θ≈40.0∘
Conclusion
The angle the rope makes with the vertical in equilibrium is approximately 40∘.
---
The forces acting on the mass are:
1. The weight of the mass (W) acting downwards, which is given by:
W=mg
where m=6kg and g=10m/s2.
Substituting the values into the weight formula:
W=mg=6kg×10m/s2=60N
In equilibrium, the vertical and horizontal components of the forces must balance out.
The vertical component of the tension must balance the weight of the mass:
Tcos(θ)=W
Substituting the weight:
Tcos(θ)=60N(1)
The horizontal component of the tension must balance the applied horizontal force:
Tsin(θ)=F
Substituting the horizontal force:
Tsin(θ)=50N(2)
Dividing equation (2) by equation (1):
Tsin(θ)Tcos(θ)=5060
This simplifies to:
tan(θ)=5060=56
To find θ, take the arctangent:
θ=tan−1(56)
θ≈40.0∘
The angle the rope makes with the vertical in equilibrium is approximately 40∘.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - conceptual problmes
45 Videos
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Very short answer questions
73 Videos
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Assertion- Reason Type Questions
17 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 NCERT Comprehension
4 Videos
- MATHEMATICAL TOOLSBOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks
5 Videos
Similar Questions
A mass of 20 kg is suspended by a rope of length 2 m from a ceiling. A force of 173.2 N in the horizontal direction is applied at the midpoint of the rope as shown in Fig. What is the angle the rope makes with the horizontal in equilibrium ? Take g = 10ms−2. Neglect mass of the rope.
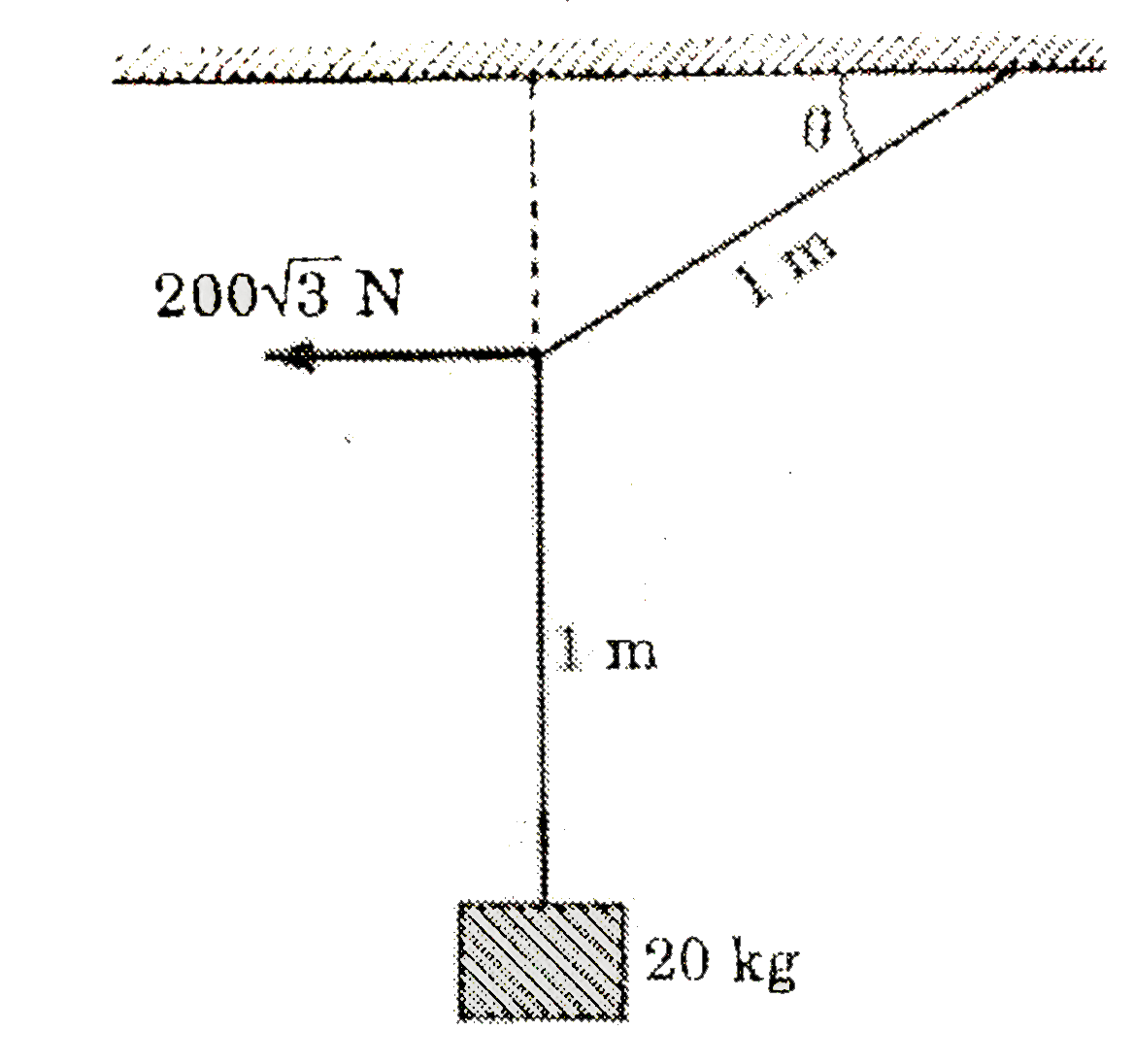
View SolutionA mass of 3kg is suspended by a rope of length 2m from the ceilling A force of 40N in the horizontal direction is applied atmidpoint P of the rope the as shown. What is the angle the rope makes with the vertical in equilibrium and the tension in part of string attached to the ceiling ? (Neglect the mass of the rope, g=10m/s2) .
View Solution
Knowledge Check
A mass of 4kg is suspended by a rope of length 4m from a ceiling. A force of 20N in the horizontal direction is applied at the mid-point of the rope as shown in figure. What is the angle which the rope makes with the vertical in equilibrium? Neglect the mass of the rope. Take g=10ms−2 .
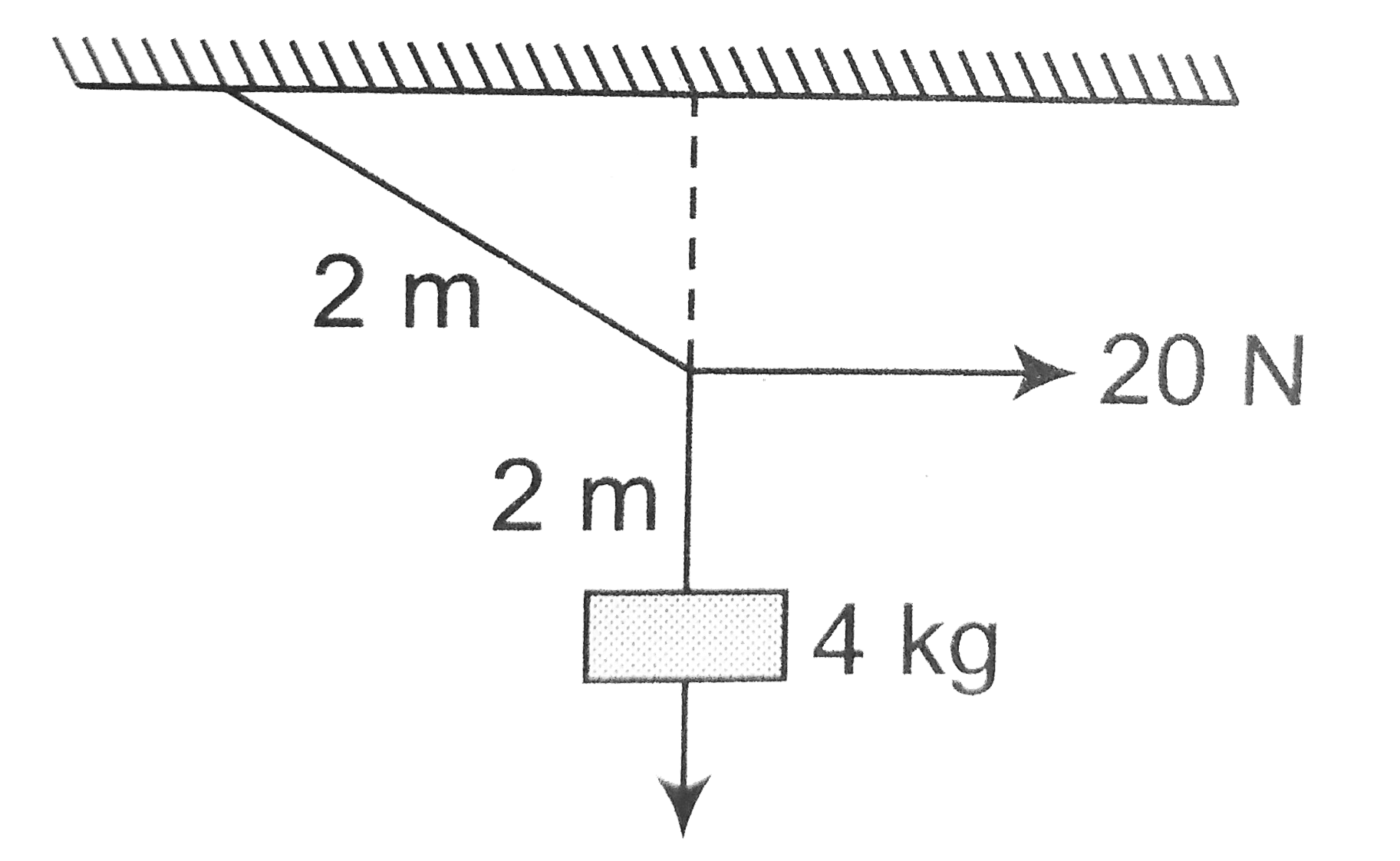 Atan−12Btan−1(12)Ctan−1√2Dtan−1(1)(√2)
Atan−12Btan−1(12)Ctan−1√2Dtan−1(1)(√2)A mass of 6 kg is suspended by a rope of length 2m from a celling. A force of 50N is applied in horizontal direction at the mid point of the rope. What is the angle of the rope with the verticle in equilibrium:-
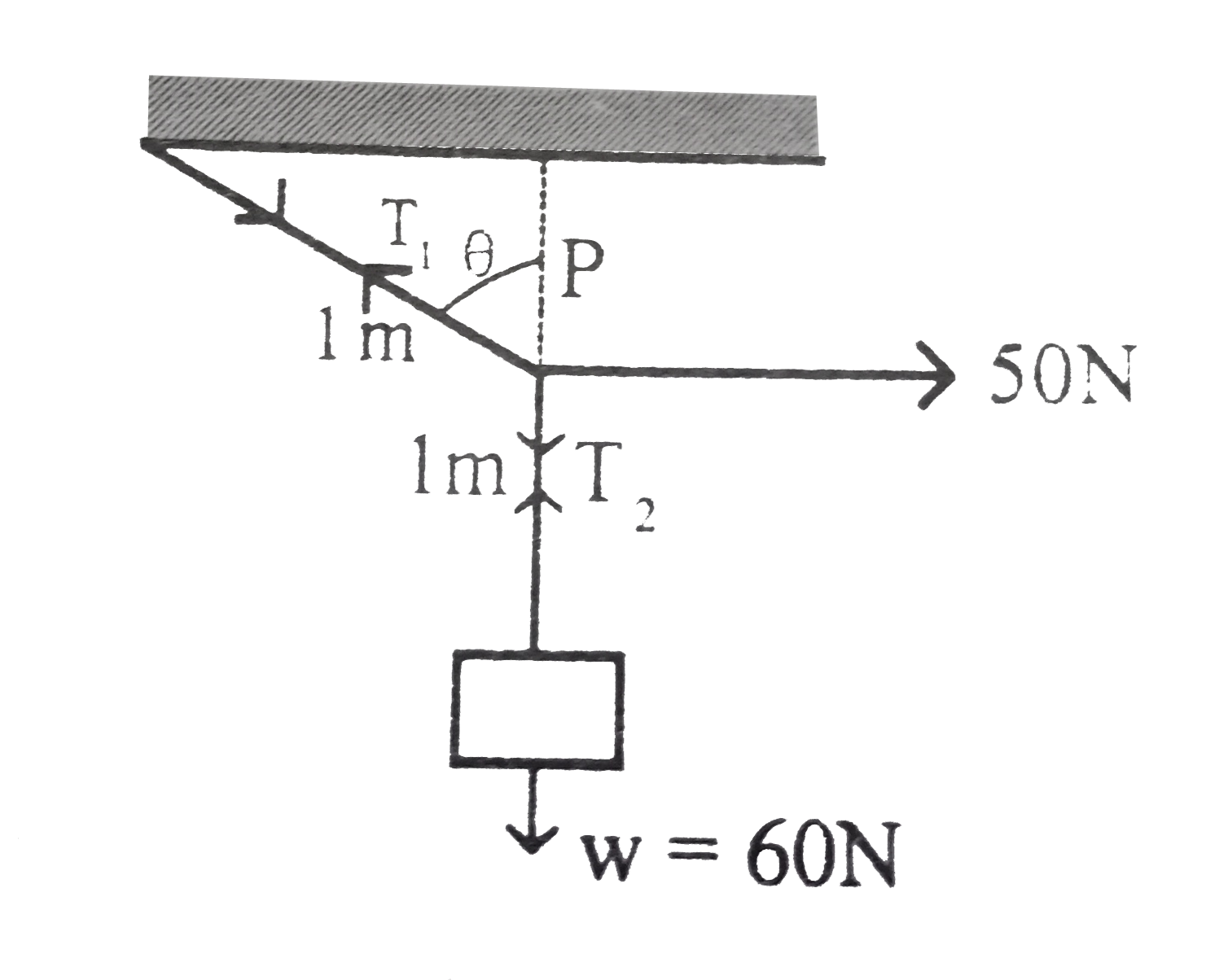 Atan−1(45)Btan−1(54)Ctan−1(56)DNone of these
Atan−1(45)Btan−1(54)Ctan−1(56)DNone of theseA block of mass 5kg is suspended by a massless rope of length 2 m from the ceiling. A force of 50 N is applied in the horizontal direction at the midpoint P of the rope, as shown in the figure. The angle made by the rope with the vertical in equilibrium is (Take g=10ms−2m .
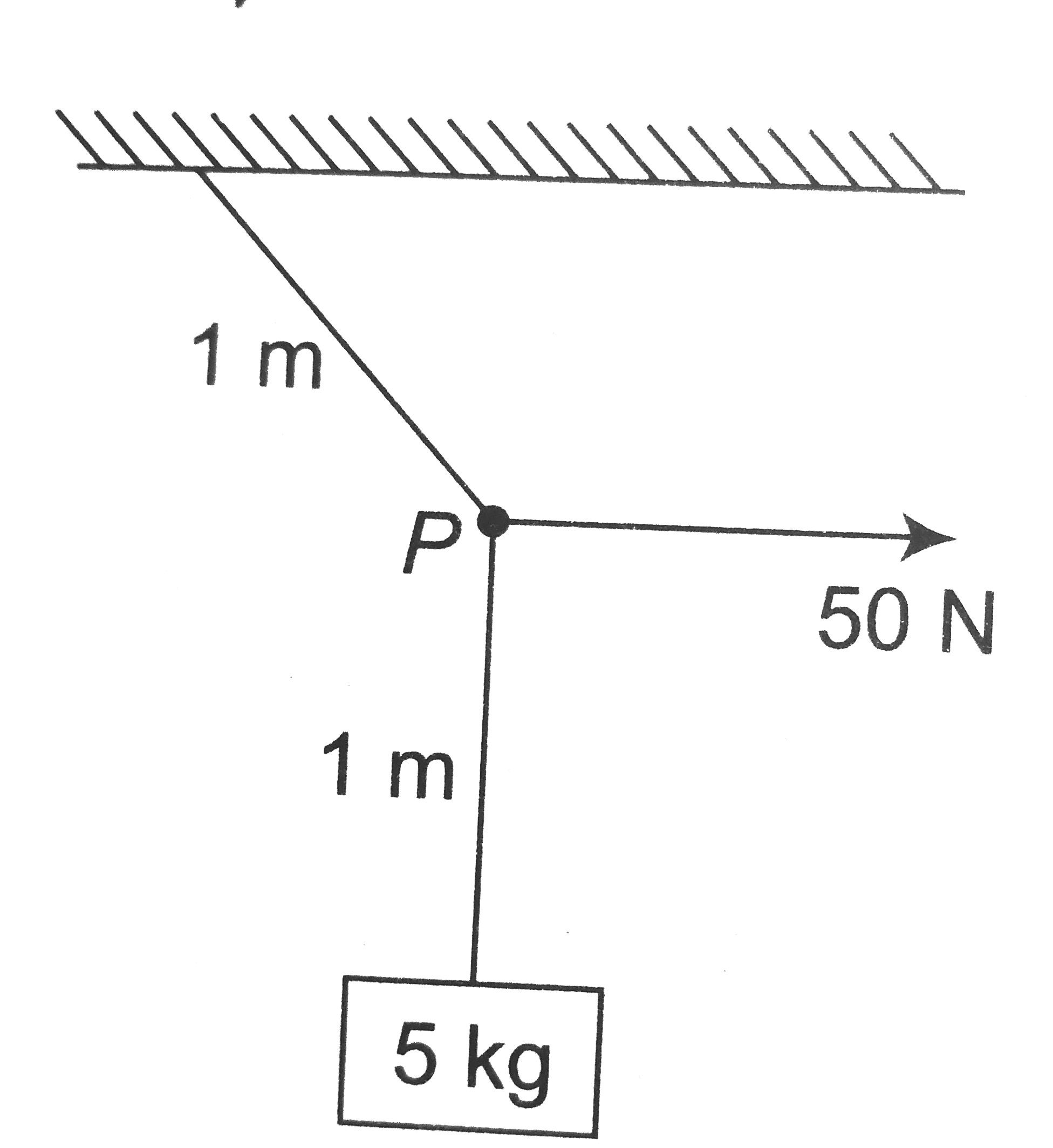 A30∘B40∘C60∘D45∘
A30∘B40∘C60∘D45∘
A mass of 3kg is suspended by a rope of length 2m from the ceiling. A force of 40 N in the horizonal direction is applied at midpoint P of the rope as shown. What is the angle the rope makes with the vertical in equilibrium and the tension in part of string attached to the ceiling? (Neglect the mass of the rope, g=10m/s2)
View SolutionA mass of 10 kg is suspended vertically by a rope of length 2 m from a ceiling. A force of 60 N is applied at the middle point of the rope in the horizontal direction, as shown in Fig. Calculate the angle the rope makes with the vertical. Neglect the mass of the rope and take g=10ms−2.

View SolutionA mass of 10 kg is suspended by a rope of length 2.8m from a ceiling. A force of 98 N is applied at the midpoint of the rope as shown in figure. The angle which the rope makes with the vertical in equilibrium is
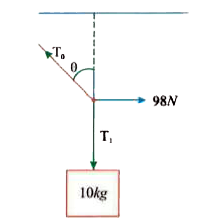
View SolutionA mass of 10kg is suspended by a rope of length 2.8m from a ceiling. A force of 98N is applied at the midpoint of the rope as shown in figure. The angle which the rope makes with the vertical in equilibrium is
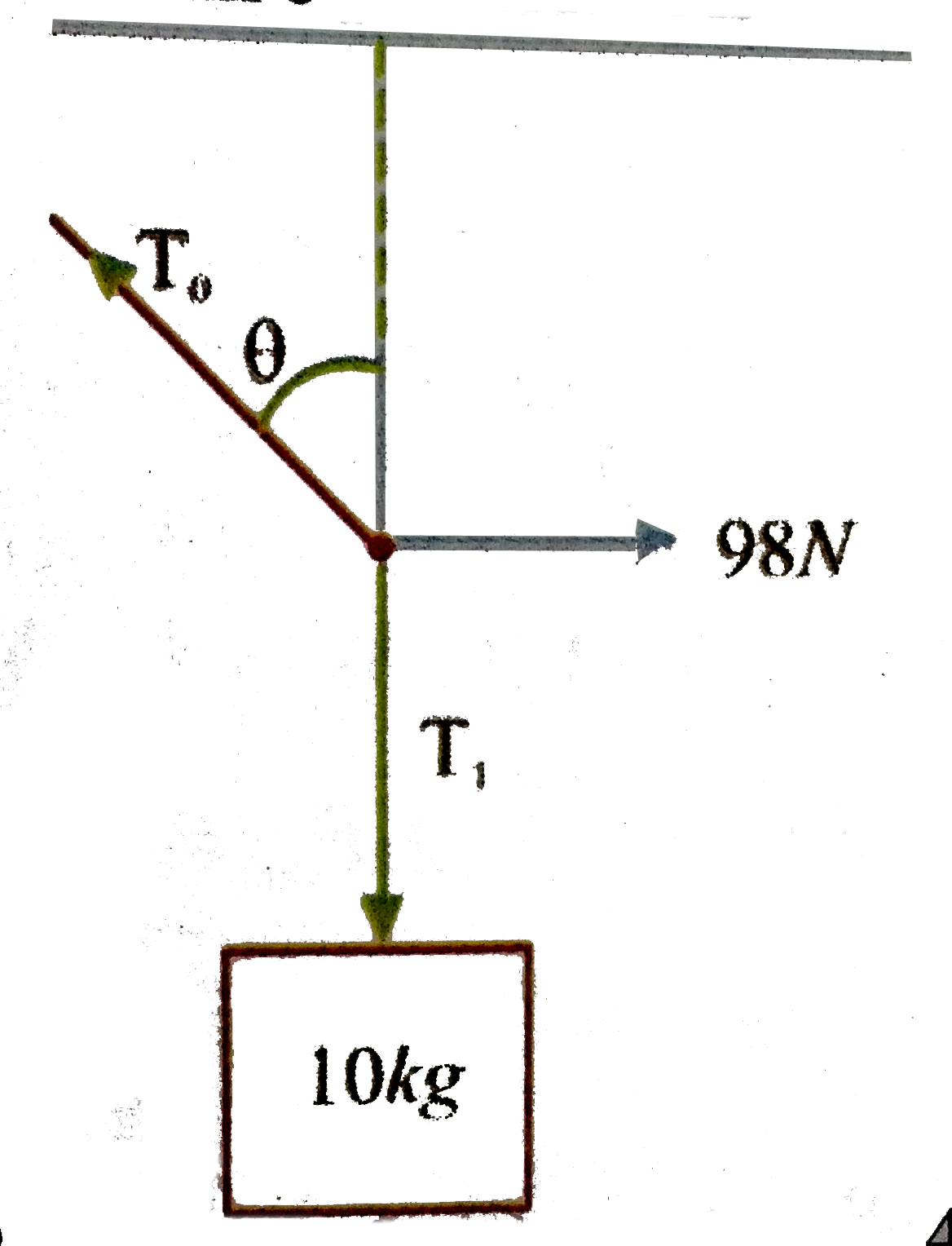 .
.
View SolutionA mass of 20 kg is suspended by a rope of length 4 m from the ceiling. A force of 60 N is applied at the midpoint of the rope in the horizontal direction. What is the angle made by the rope with the vertical in equilibrium? Assume that the mass of the rope is negligible and g=10m/s2
View Solution
