A mass of mass 60kg is pulling a mass M by an inextensible light rope passing through a smooth and massless pulley as shown in figure. The coefficient of friction between the mass and ground is μ=1/2 find the maximum value of M that can be pulled on the ground

T=Mg(T= tension in the rope)
N=60g−Tsin60∘(N is normal reaction between the man and the ground) and Tcos60∘=μN
Solving these three equations with proper substitutions, we get
M=120√3+2kg
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.216videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.327videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Solved Examples12videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer5videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
Similar Questions
A block of mass m = 2kg is accelerating by a force F = 20N applied on a smooth light pulley as shown in the figure. If the coefficient of kinetic friction between the block and the surface is μ=0.3, find its acceleration.
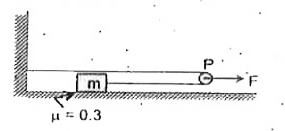 View Solution
View SolutionTwo masses of 10 kg and 20 kg are connected with an inextensible string passing over two smooth pulleys as shown in the figure. The acceleration of 20 kg mass will be :
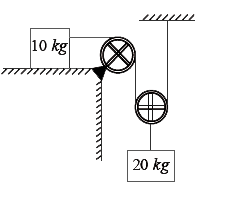 View Solution
View Solution
Knowledge Check
- Question 1 - Select One or More
Two masses m and M(m<M) are joined by a light string passing over a smooth and light pulley (as shown)
 Athe acceleration of each mass is (M−mM+m)gBthe tension in the string connecting masses is (2MmM+m)gCthe thrust acting on the pulley is (4MmM+m)gDNone of the above
Athe acceleration of each mass is (M−mM+m)gBthe tension in the string connecting masses is (2MmM+m)gCthe thrust acting on the pulley is (4MmM+m)gDNone of the above - Question 2 - Select One
A block of mass m is placed on the top of another block of mass M as shown in the figure. The coefficient of friction between them is μ.

The maximum acceleration with which the block M may move so that m also moves along with it isAμgBμMmgCμmMgDgμ - Question 3 - Select One
Two blocks of masses m1 and m2 are connected through a massless inextensible string .A block of mass m1 is placed at the fixed rigid inclined surface while the block of mass m2 hanging at the other end of the string which is passing through a fixed massless frictionless pulley shown in figure The coefficient of static friction between the block and the inclined plane is 0.8 The system of masses m1 and m2 released from rest
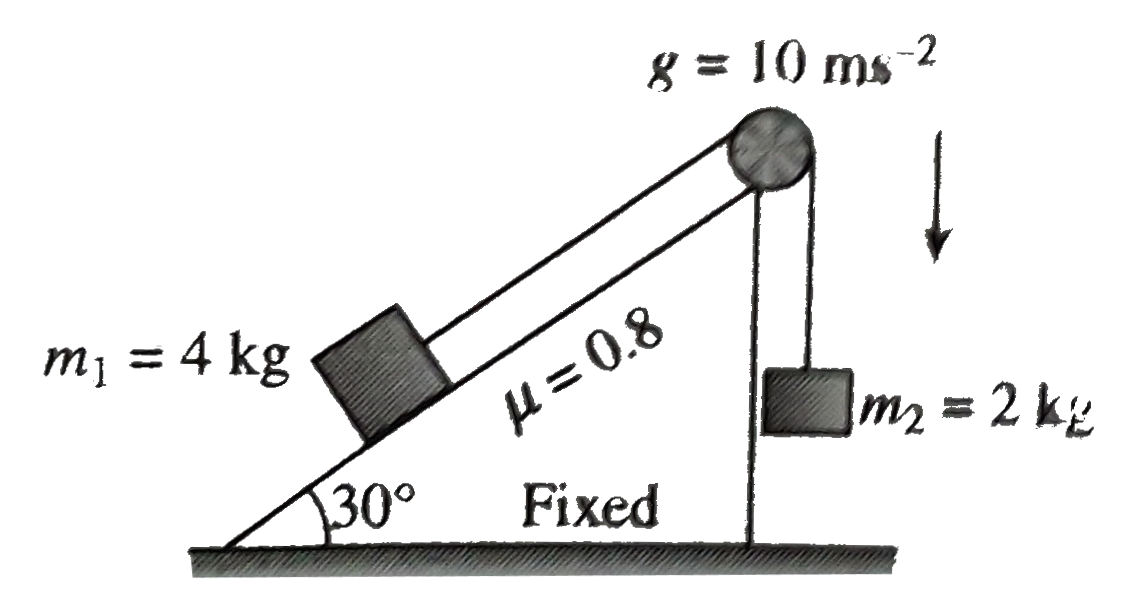 AThe tension in the string is 20N after releasing the systemBThe contact force by the inclined surface on the block in along normal to the inclined surfaceCThe magnitude of contact force by the inclined surface on the m1 is 20√3NDNone of these
AThe tension in the string is 20N after releasing the systemBThe contact force by the inclined surface on the block in along normal to the inclined surfaceCThe magnitude of contact force by the inclined surface on the m1 is 20√3NDNone of these
A block A of massm which is placed a rough inclined face of a wedge of same mass being pulled through light string and with force F as shown in figure The coefficient of friction between inclined face and block A is μ while there is no friction between the ground and wedge it the whole system moves with same acceleration then find the value of F
 View Solution
View SolutionA body of mass 20 kg is moving on a rough horizxontal plane. A block of mass 3 kg is connected to the 20 kg mass by a string of negligible mass through a smooth pulley as shown in the figure. The coefficient of kinetic friction between the heavier mass and teh surface is
(g=10m/s2).
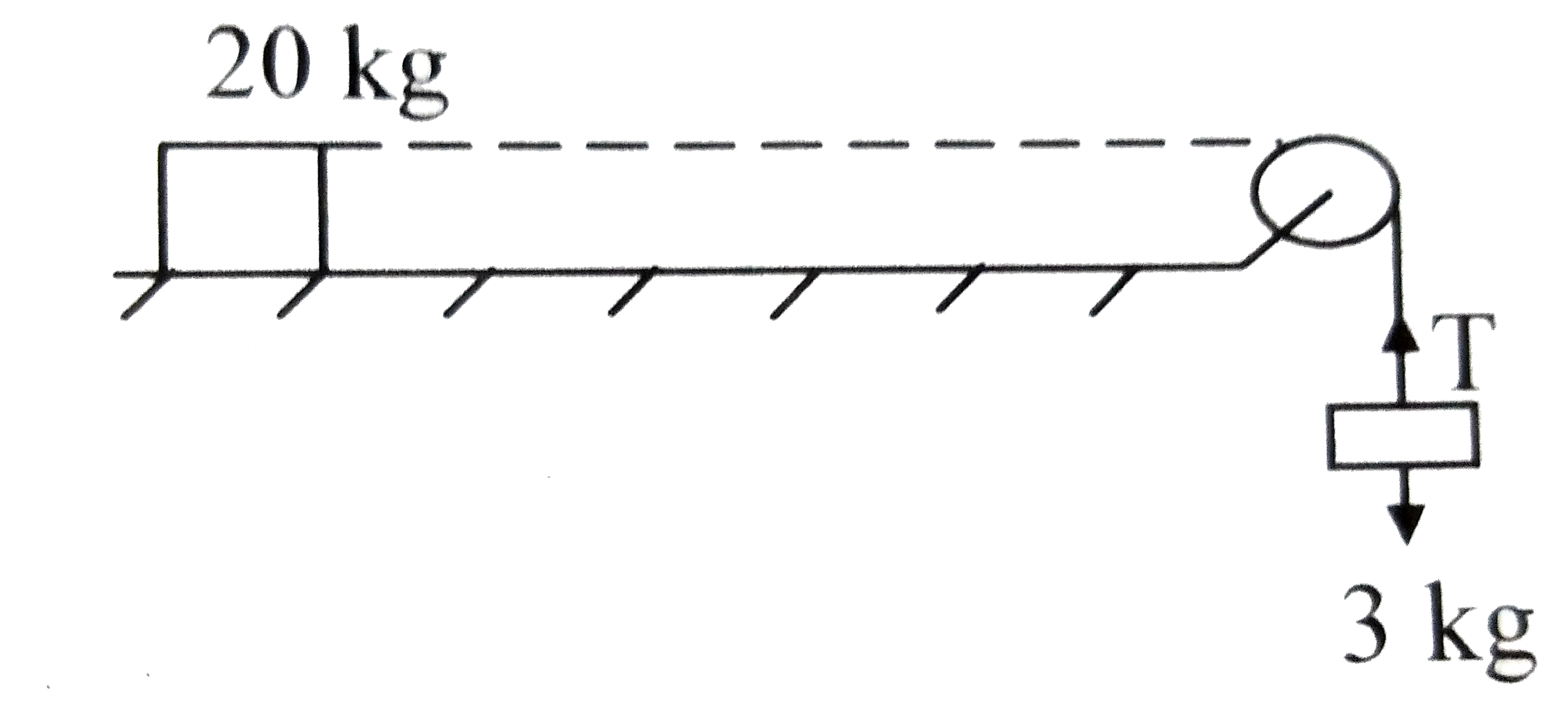 View Solution
View SolutionFind the acceleration of the block of mass M in the situation of figure. The coefficient of friction between the two blocks is μ1 and that between the bigger block and the ground is μ2.
View SolutionA particle of mass m connected with a hanging bob of mass M by an inextensible string is stationary relative to the rotating platform . The coefficient of static friction between the particle and platform is μ

Find the
a. maximum angular speed ω1
b. maximum angular speed ω2
(forM>μm)View SolutionA particle of mass m is pulled along an arbitrary curved surface without acceleration as shown in figure. Coefficient of friction between surface and particle is μ. Then


codes:View Solution

