An insect craws up a hemispherical surface very slowly (see fig.). The coefficient of friction between the insect and the surface is 1/3. If the line joining the center of the hemispherical surface to the insect makes an angle α with the vertical, the maximum possible value of α is given by

From FBD friction f=mgsinα
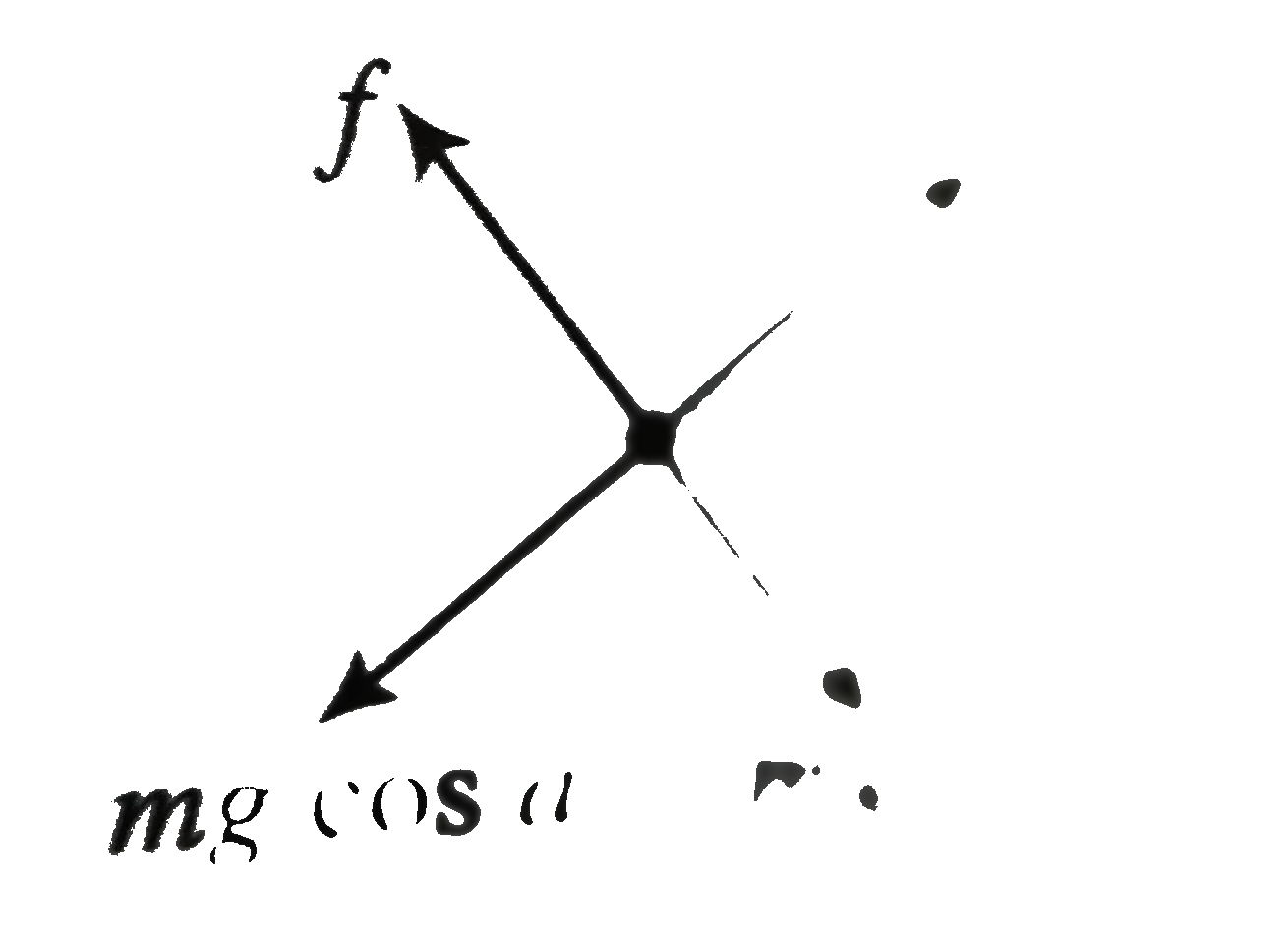
N=mgcosαfN=tanα
For the maximum value of α the friction limiting friction , so
μ=tanα⇒cosα=3
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.216videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.327videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Solved Examples12videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer5videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
Similar Questions
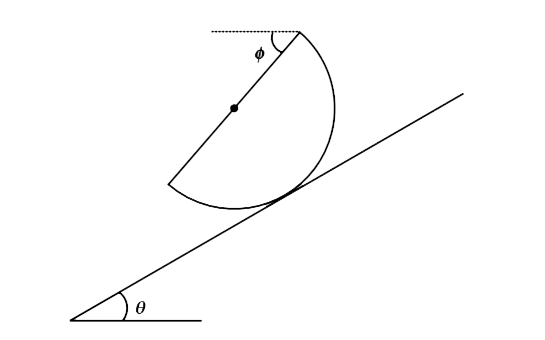
A uniform hemisphere placed on an incline is on verge of sliding. The coefficient of friction between the hemisphere and the incline is μ=0.3.
Find the angle ϕ that the circular base of the hemisphere makes with the horizontal.
Given sin(tan−10.3)≅0.29 and sin−1(0.77)≅50∘
 View Solution
View SolutionA crate is pulled along a horizontal surface at constant velocity by an applied force F that makes an angle θ with the horizontal. The coefficient of kinetic friction between the crate and the surface is μ. Find the angle θ such that the applied force is minimum to slide the block. Also find the minimum value of this force.
View Solution
Knowledge Check
- Question 1 - Select One
An insect crawls up a hemispherical surface very slowly (see the figure). The coefficient of friction between the insect and the surface is 1/3. If the line joining the centre of the hemispherical surface to the insect makes an angle α with the vertical, the maximum possible value of α is given by
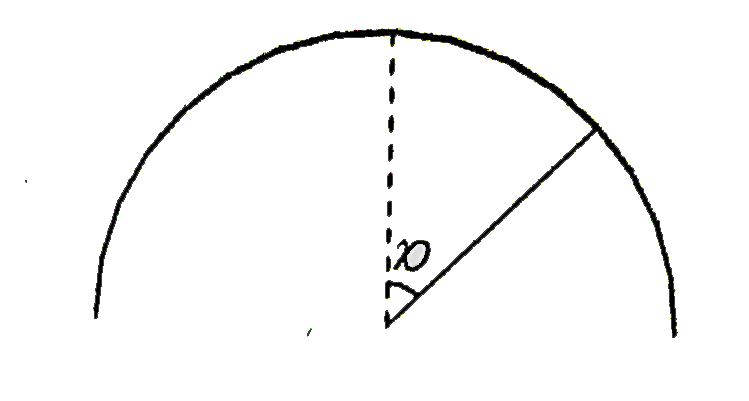 Acotα=3Btanα=3Csecα=3Dcosecα=3
Acotα=3Btanα=3Csecα=3Dcosecα=3 - Question 2 - Select One
The coefficient of friction between an insect and a hemispherical bowl of radius r is μ. The maximum height to which the insect can crawl in the bowl is
Ar√1+μ2Br[1−1√1+μ2]Cr√1+μ2Dr[√1+μ2−1] - Question 3 - Select One
The coefficient of friction between a hemispherical bowl and an insect is √0.44 and the radius of the bowl is 0.6m. The maximum height to which an insect can crawl in the bowl will be
A0.4mB0.2mC0.3mD0.1m
A rectangular block is kept on a rough horizontal surface and given some initial velocity. The coefficient of friction between the block and the surface is constant. The block will topple O either at the very beginning or not at all just before coming to rest only if the coefficient of friction at the ground O is > 1 only if some external force acts on it in addition to the frictional force
View SolutionThe coefficient of friction between a hemispherical bowl and an insect is √0.44 and the radius of the bowl is 0.6m. The maximum height to which an insect can crawl in the bowl will be .
View Solution
An insect of mass m, starts moving on a rough inclined surface from point A. As the surface is vert sticky, the corfficient of fricion between the insect and the incline is μ=1. Assume that it can move in any direction, up the incline or down the incline thenView SolutionA particle is placed at rest inside a hollow hemisphere of radius R. The coefficient of friction between the particle and the hemisphere is μ=1√3. The maximum height up to which the particle can remain stationary is
View Solution
A solid sphere of mass m and radius R is rolling without slipping on a rough horizontal surface with angular acceleration α. Centre of mass of sphere lies at a distance R√2 from the centre of sphere. Find the normal force applied by sphere on the surface at an instant when line joining centre of mass of sphere and centre of sphere makes an angle 45∘ with the vertical and angular velocity of sphere at this instant is ω.View Solution

