A massless, inextensible string is wrapped round the circumference of a disc of mass M and radius R. The second end of the string is tied to a m which stands at vertical height 'h' from the ground initially. What will be the velocity of mass m when it is released and it touches the ground?

√2gh
√2gh.Mm
√2gh×mM
(4mgh×1M+2m)1/2
The correct Answer is:D
Here the equation of motion for connected bodies will be
mg−T=ma …(i)
and τ=12MR2.aR
T.R.=12MRa
or T=12Ma ...(ii)
from (i) and (ii) mg=(M2+m)a
or a=2mgM+2m
Now v=√2ah=√4mghM+2m
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - ROTATIONAL MOTIONEXERCISE - LEVEL-III (MCQ)
10 Videos
- ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - ROTATIONAL MOTIONEXERCISE - RCQ
8 Videos
- ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - ROTATIONAL MOTIONEXERCISE - RCQ
8 Videos
- RAY OPTICSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICSEXERCISE - RECENT COMPETITIVE QUESTION
32 Videos
- SOLIDS & SEMICONDUCTOR DEVICESBOOK - MODERN PUBLICATIONCHAPTER - SOLIDS & SEMICONDUCTOR DEVICESEXERCISE - Revision Test
28 Videos
Similar Questions
An ideal inextensible string is wrapped over the disc of mass m and radius R. The other end of the string is connected to mass m. the string is passing over an ideal pulley A as shown in the figure. At any time t, mass m and disc are moving downward with acceleration of magnitude a1 and a2 respectively. The disc is rotating clockwise with angular acceleration of magnitude α . There is no slipping betweeb string and disc. choose the incorrect option
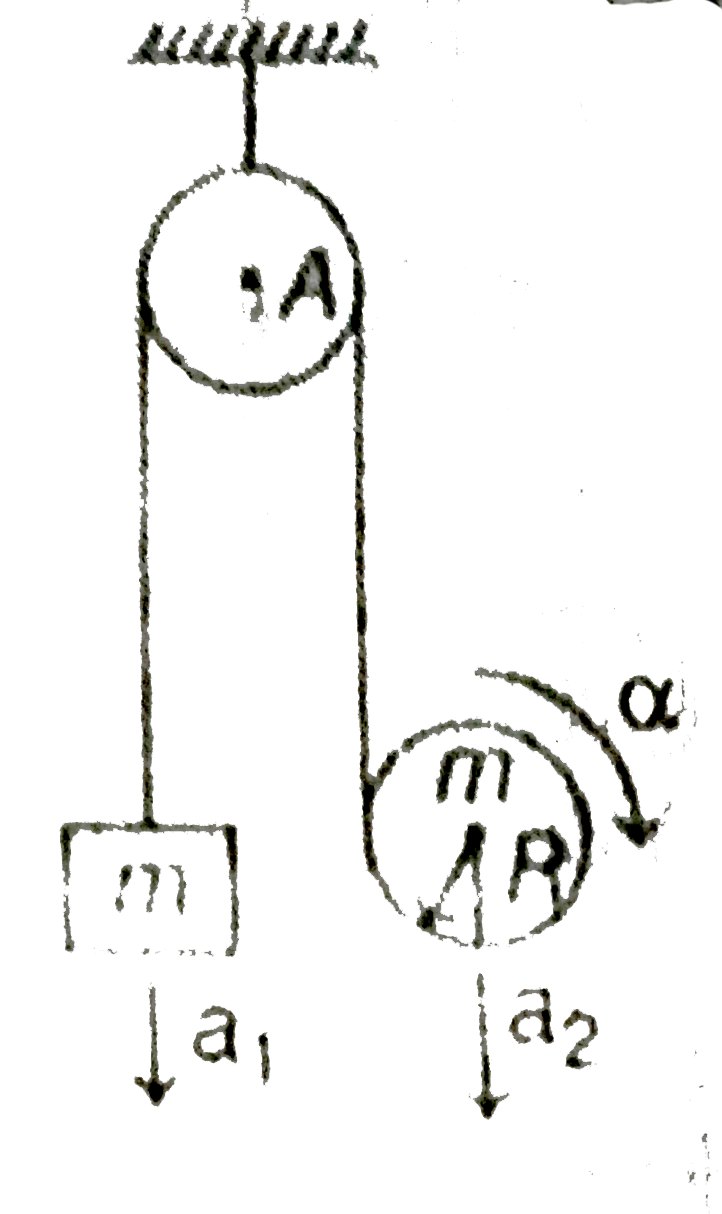
View SolutionA string of negligible mass is wrapped on a cylindrical pulley of mass M and radius R. The other end of string is tied to a bucket of mass m. If the pulley rotates about a horizontal axis then the tension in the string is :
View Solution
Knowledge Check
A massless rope is wrapped several times on a disc of mass M and radius R. The other end is tied to a mass m which at the beginning is at a height of h above ground as shown in the figure. When released the velocity of the mass as it touches the ground is
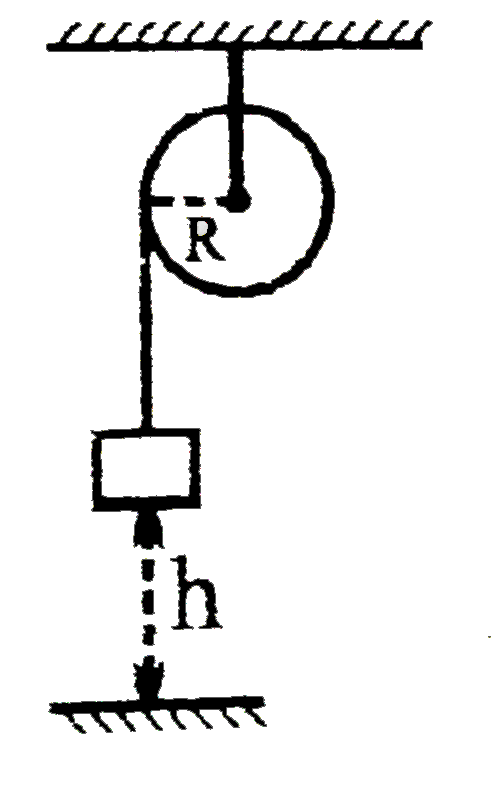 A√4mgh2m+MB√2ghC√4mgh3MD√4mghM+m
A√4mgh2m+MB√2ghC√4mgh3MD√4mghM+mA massless rope is wrapped several times on a disc of mass M and radius R. The other end is tied to a mass m which at the beginning is at a height of h above ground as shown in the figure. When released the velocity of the mass as it touches the ground is
 A√2ghB√2ghMmC√2ghm/MD√4gh/2m+M
A√2ghB√2ghMmC√2ghm/MD√4gh/2m+MAn ideal inextensible string is wrapped over the disc of mass m and radius R. The other end of the string is connected to mass m. the string is passing over an ideal pulley A as shown in the figure. At any time t, mass m and disc are moving downward with acceleration of magnitude a1 and a2 respectively. The disc is rotating clockwise with angular acceleration of magnitude α . There is no slipping betweeb string and disc. choose the incorrect option
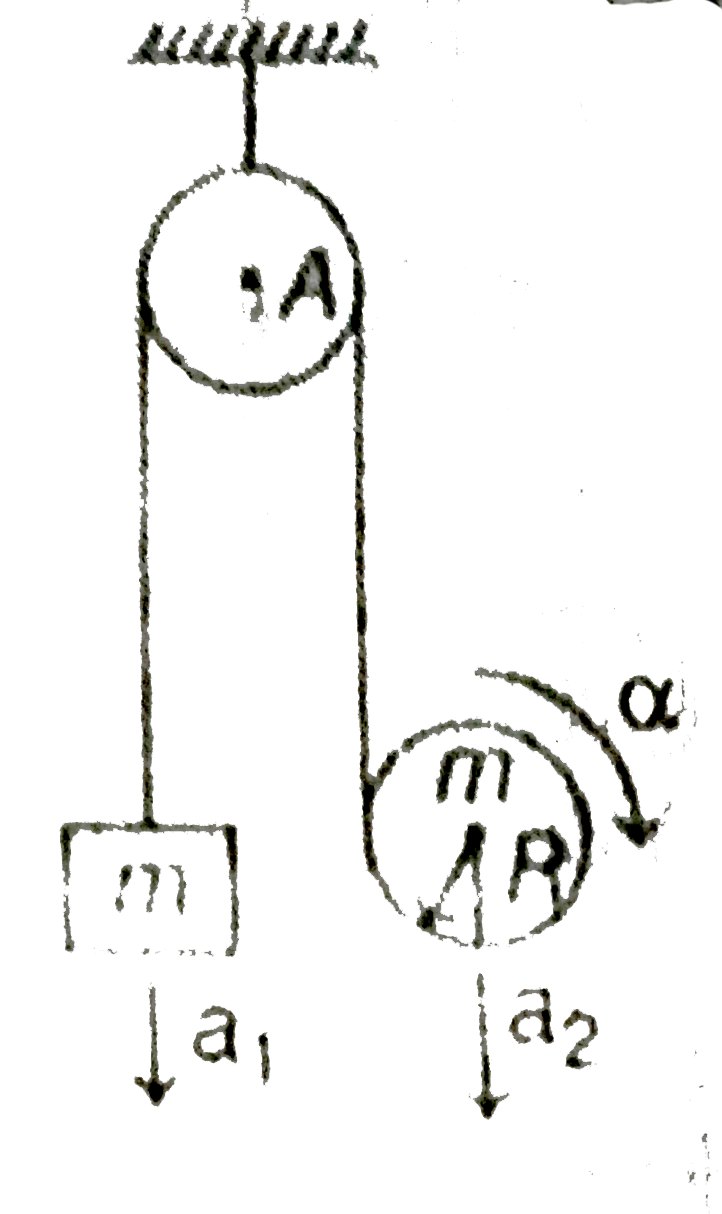 Aa1=a2BαR>a1CαR=a1DαR<a2
Aa1=a2BαR>a1CαR=a1DαR<a2
A string wrapped around a cyliner of mass m and radius R. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
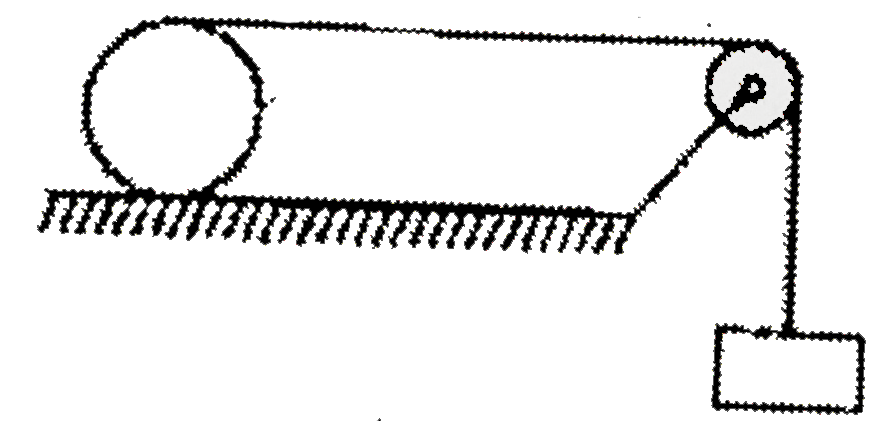
Velocity of point of contact 'of cylinder at this moment is:
View SolutionA string wrapped around a cyliner of mass m and radius R. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
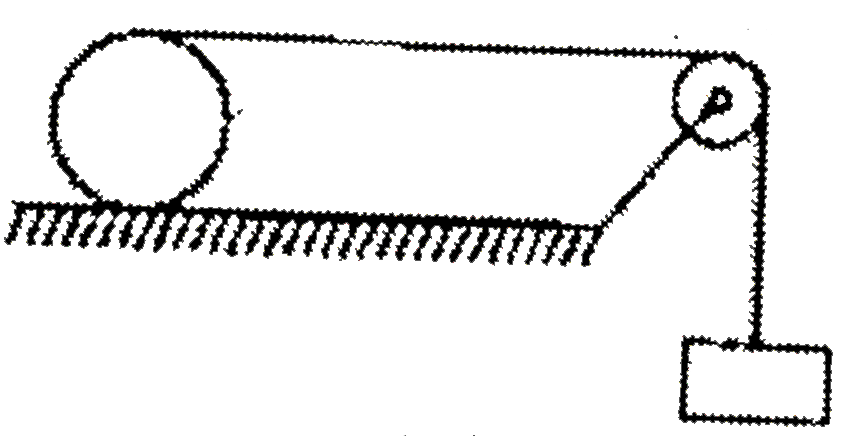
Velocity of hanging block at this moment is: is:
View SolutionA string wrapped around a cyliner of mass m and radius R. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
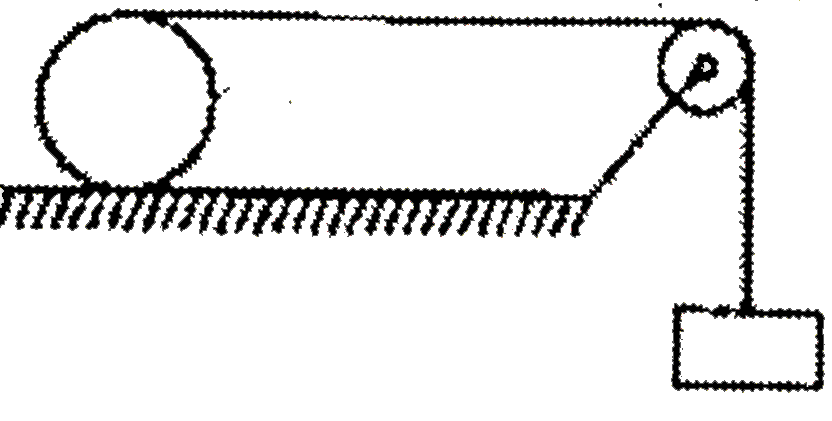
Acceleration of hanging mass is:
View SolutionA string wrapped around a cyliner of mass m and radius R. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
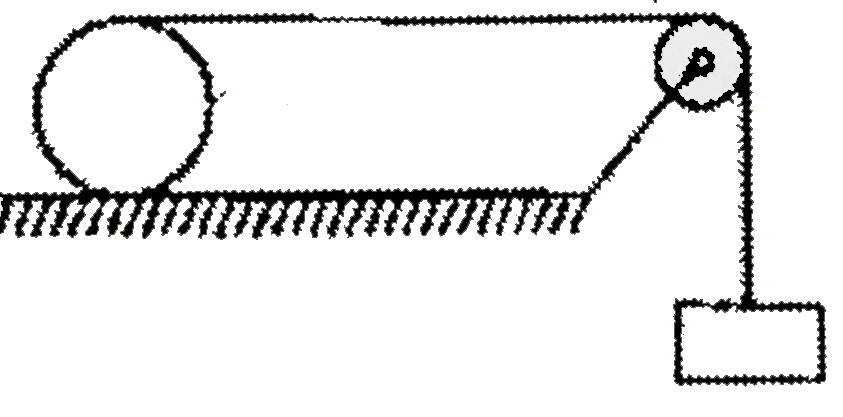
Acceleration of cylinder is:
View SolutionA string is wrapped around a cylinder of mass M and radius R. The string is pulled vertically upwards to prevent the centre of mass from falling as the cylinder unwinds the string. The tension in the string is
View Solution
