A massless rod of kngth L is suspended by two identical strings AB and CD of equal length. A block of mass m is suspended from point O such that BO is equal to 'x'. Further it is observed that the frequency of 1st harmonic in AB is equal to 2nd harmonic frequency in CD, 'x' is

L5
4L5
3L4
L4
The correct Answer is:A
Frequency of the first harmonic of
AB=12l√TABm
Frequency of the 2nd harmonic of
CD=1l√TCDm
Given that the two frequencies are equal.
∴12l√TABm=1l√TCDm⇒TAB4=TCD
⇒TAB=4TCD
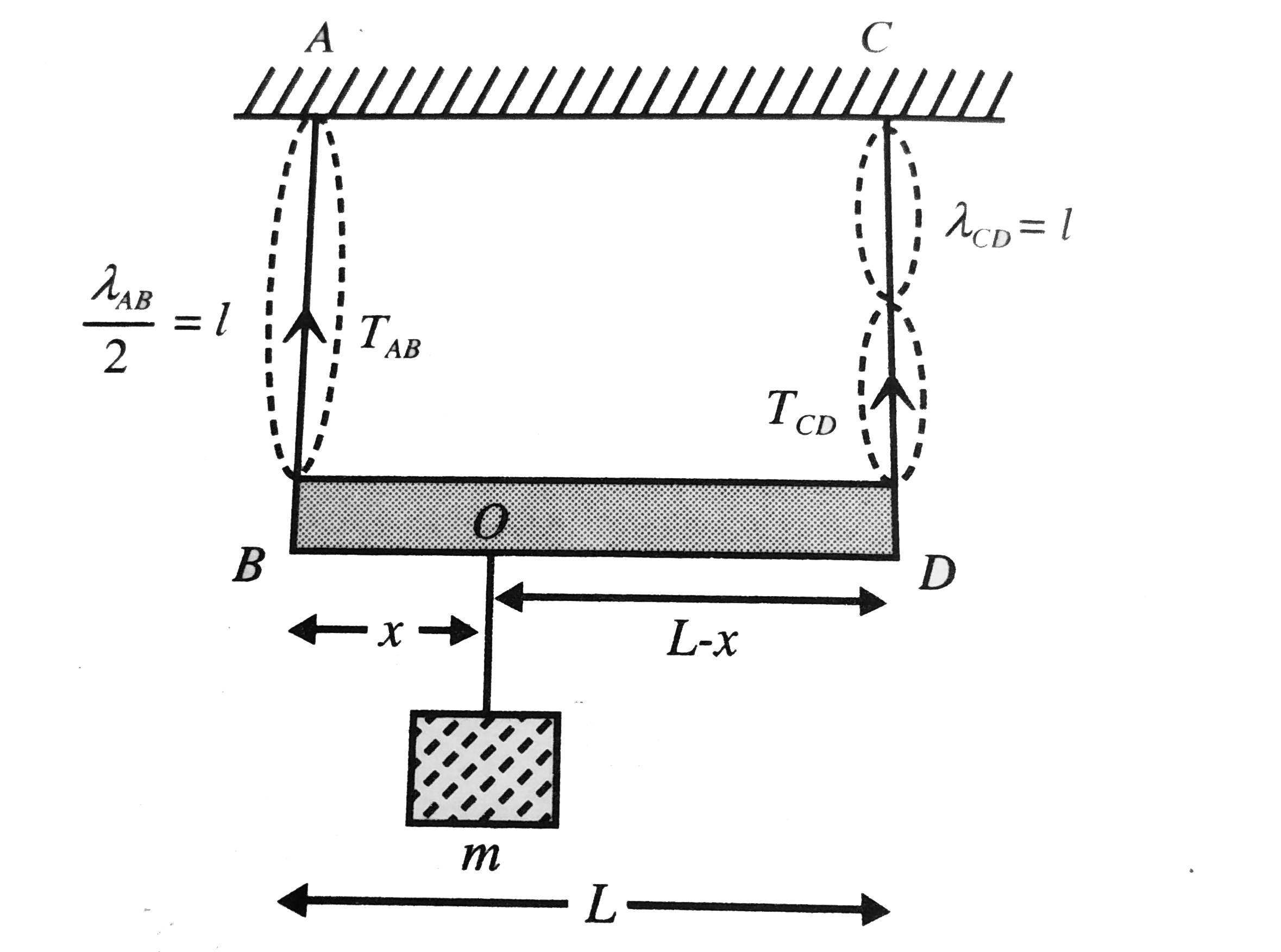
For rotational of massless rod taking torque about point O,
TAB×x=TCD(L−x)
Solve to get x=L5.
Topper's Solved these Questions
- ARCHIVES 2 VOLUME 6BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ARCHIVES 2 VOLUME 6EXERCISE - Multiple Correct
22 Videos
- ARCHIVES 2 VOLUME 6BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ARCHIVES 2 VOLUME 6EXERCISE - Comprehension
12 Videos
- ARCHIVES 2 VOLUME 6BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ARCHIVES 2 VOLUME 6EXERCISE - True/False
4 Videos
- ARCHIVES 1 VOLUME 6BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ARCHIVES 1 VOLUME 6EXERCISE - Integer
4 Videos
- BASIC MATHEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.6
20 Videos
Similar Questions
A massless rod of length L is suspened by two identical string AB and CD of equal length. A block of mass m is suspended from point O such that BO is equal to 'x'. Further it is observed that the frequency of 1st harmonic in AB is equal to 2nd harmonic frequency in CD. 'x' is
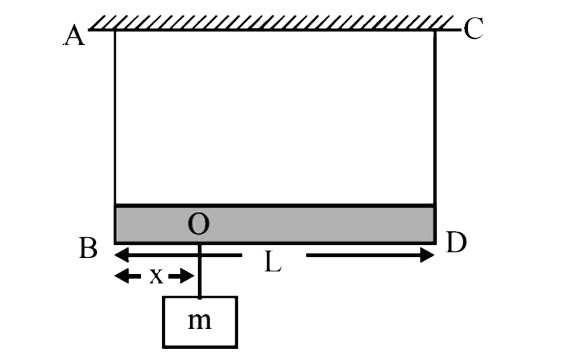
View SolutionA massless rod BD is suspended by two identical massless strings AB and CD of equal lengths. A block of mass m is suspended at point P such that BP is equal to x, If the fundamental frequency of the left wire is twice the fundamental frequency of right wire, then the value of x is :-
_E01_188_Q01.png)
View Solution
Knowledge Check
A massless rod of length L is suspened by two identical string AB and CD of equal length. A block of mass m is suspended from point O such that BO is equal to 'x'. Further it is observed that the frequency of 1st harmonic in AB is equal to 2nd harmonic frequency in CD. 'x' is
 AL5B4L5C3L4DL4
AL5B4L5C3L4DL4
A point mass m is suspended at the end of a massless wire of length l and cross section. If Y is the Young's modulus for the wire, obtain the frequency of oscillation for the simple harmonic motion along the vertical line.
View SolutionA block of mass 3m is suspended by a meter scale rod of mass m as shown in figure. If the tension in the string A is equal to kmg in equilibrium, then value of k will be
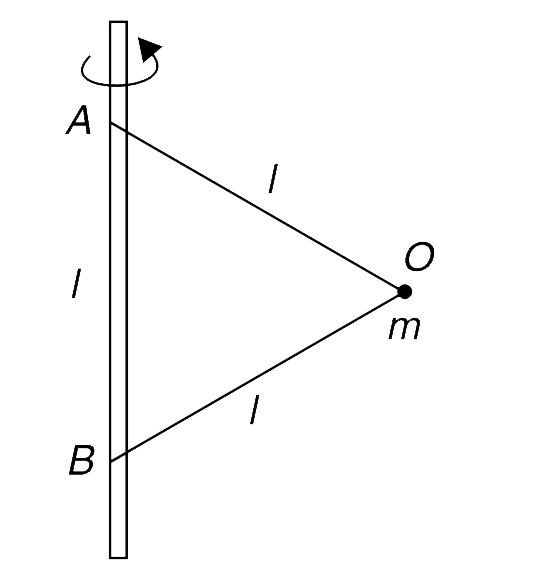
View SolutionA particle of mass m is attached to a vertical rod with two inextensible strings AO and BO of equal lengths l. Distance between A and B is also l. The setup is rotated with angular speed ω with rod as the axis.
View SolutionA block of mass M suspended from a spring oscillates with time period T. If spring is cut in to two equal parts and same mass M is suspended from one part, new period os oscillation is
View SolutionA block of mass M suspended from a spring oscillates with time period T. If spring is cut in to two equal parts and same mass M is suspended from one part, new period os oscillation is
View Solution
A uniform rod AB is suspended from a point X, at a variable distance x from A, as shown. To make the rod horizontal , a mass m is suspended from its end A. A set of (m,x) value is recorded that give a straight line, when plotted, are :
View SolutionTwo identical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
View Solution
