A metal piece of mass 160 g lies iln equilibrium inside a glass of water figure. The ppece touches the bottom of the glass at a small number of points. If the density of the metl is 8000 kg m−3, find the normal fore exerted by the bottom of the glass on the metal piece.

2N
8N
0.16N
1.4N
The correct Answer is:D
As the piece touches the glass at small number of points, water would be there at the bottom of the piece also and hecne buoyancy acts on it.
From equilibrium condition mg=FB+N
FB=Vρwaterg=mρmetal×ρwater×g
=0.168×10=0.2N
So, N=mg−FB=1601000×10−0.2=1.4N
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Multipe Correct15videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Assertion-Reasoning8videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Subjective25videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE1videos
GRAVITATION
Similar Questions
A metal piece of mass 160 g lies in equilibrium inside a glass of water as shown in figure. The piece touches the bottom of the glass at a small number of points. If the density of the metal is 8000kgm−3, find the normal fore exerted by the bottom of the glass on the metal piece.
 View Solution
View SolutionThe volume of a piece of metal is 50 cm3. If the density of metal is 2.5 g cm−3, find the mass of metal.
View SolutionA glass full of water has a bottom of area 20cm2, top of area 20cm, height 20cm and volume half a litre.
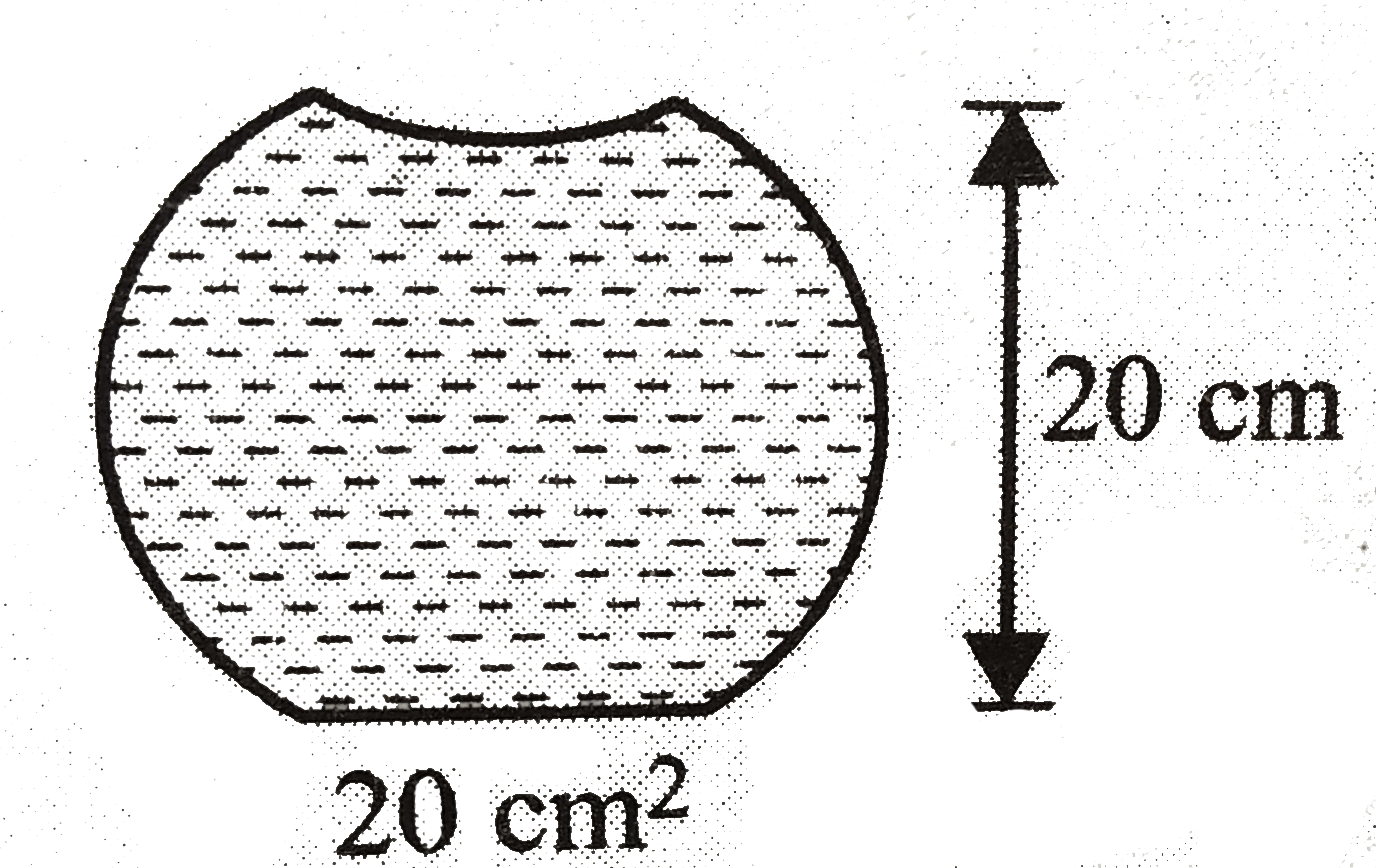
a. Find the force exerted by the water on the bottom.
b. Considering the equilibrium of the v, after. find the resultant force exerted by the side, of the glass on the water. Atmospheric pressure =1.0×105N/m2. Density of water =1000kg/m−3 and g=10m/s2View SolutionA piece of iron has a volume of 25cm3 and mass 195 g. Find the density of iron in kgm−3
View SolutionA curved glass vessel full of water upto a height of 10 cm has a bottom of area 10cm2, top of area 30cm2 and volume 1 L.
(i) Find the force exerted by the water on the bottom.
(ii) Find the resultant force exerted by the sides of the glass on the water.
(iii) If the glass vessel is covered by a jar and the air inside the jar is completely pumped out, what will be the answers to parts (a) and (b)
(iv) If a glass vessel of different shape is used provided the height, the bottom area and the volume are unchanged, will the answers to parts (a) and (b) change.
(Take, g=10ms−2 , density of water =103kgm−2 and atmospheric pressure =1.01×105Nm−2)View SolutionA glass full of water upto a height of 10 cm has a bottom of are 10cm2, top of area 30cm2 and volume 1 litre.
(a) Find the force exerted by the water on the bottom.
(b) Find the resultant force exerted by the sides of the glass on the water.
(c ) If the glass is convered by a jar and the air inside the jar is completely pumped out, what will be the answer to parts (a) and (b).
(d) If a glass of different shape is used, provided the height, the bottom area, the top area and the volume are unchanged, will the answer to parts (a) and (b) change.
Take g=10m/s3, density of water=103kg/m3 and atmospheric pressure =1.01×105N/m2.View SolutionA piece of brass of volume 30cm3 has a mass of 252 g. Find the density of brass in kgm−3
View SolutionThe mass of a lead piece is 115 g. When it is immersed into a measuring cylinder, the water level rises from 20 mL mark to 30 mL mark. Find the density of the lead in kg m−3
View SolutionA calorimeter of mass 50 g and specific heat capacity 0.42Jg−1∘C−1 contains some mass of water at 20°C. A metal piece of mass 20 g at 100∘C is dropped into the calorimeter. After stirring, the final temperature of the mixture is found to be 22∘C. Find the mass of water used in the calorimeter.
[specific heat capacity of the metal piece = 0.3Jg−1∘C−1
specific heat capacity of water = 4.2Jg−1∘C−1]View SolutionAn ideal massles spring S can be compressed 1 m by a force of 100 N in equilibrium. The same spring is placed at the bottom of a frictionless plane inclined at 30∘ to the horizontal. A 10 kg block M is released from rest at the top of the incline and is brought to rest momentarily after compressing the spring by 2 m. If g=10m/s2, the speed of mass just before it touches the spring is √10xm/s. Find value of x?
 View Solution
View Solution

