A large wooden piece in the form of a cylinder floats on water with two-thirds of its length immersed. When a man stands on its upper surface, a further one-sixth of its length is immersed. The ratio between the masses of the man and the wooden piece is
1:2
1:3
1:4
1:5
The correct Answer is:C
To solve the problem, we need to analyze the situation using the principles of buoyancy and the relationship between the weight of the displaced water and the weight of the floating object.
1. Understanding the Initial Condition:
- Let the length of the wooden cylinder be L.
- The volume of the wooden piece that is submerged when it is floating is 23L.
- The volume of the wooden piece can be expressed as Vwood=A⋅L, where A is the cross-sectional area.
2. Calculating the Weight of the Wooden Piece:
- The weight of the wooden piece is equal to the weight of the water displaced by the submerged portion.
- The volume of water displaced is Vdisplaced=A⋅23L.
- The weight of the displaced water is given by:
Wdisplaced=Volume×Density of water×g=A⋅23L⋅ρwater⋅g
- Therefore, the weight of the wooden piece is:
Wwood=mwood⋅g=A⋅23L⋅ρwater⋅g
3. Condition When the Man Stands on the Wooden Piece:
- When the man stands on the wooden piece, an additional 16L of the cylinder is submerged.
- The total submerged length now is 23L+16L=46L+16L=56L.
- The volume of water displaced now is:
Vdisplaced new=A⋅56L
- The weight of the displaced water is now:
Wdisplaced new=A⋅56L⋅ρwater⋅g
4. Setting Up the Equation:
- The total weight when the man is standing on the wooden piece is the weight of the wooden piece plus the weight of the man:
mwood⋅g+mman⋅g=A⋅56L⋅ρwater⋅g
- Dividing through by g gives:
mwood+mman=A⋅56L⋅ρwater
5. Equating the Two Conditions:
- From the first condition, we have:
mwood=A⋅23L⋅ρwater
- Substitute mwood into the equation from step 4:
A⋅23L⋅ρwater+mman=A⋅56L⋅ρwater
6. Solving for the Mass of the Man:
- Rearranging gives:
mman=A⋅56L⋅ρwater−A⋅23L⋅ρwater
- Converting 23 to a fraction with a denominator of 6:
23=46
- Thus, we have:
mman=A⋅L⋅ρwater(56−46)=A⋅L⋅ρwater⋅16
7. Finding the Ratio of Masses:
- Now we can find the ratio of the mass of the man to the mass of the wooden piece:
mmanmwood=A⋅L⋅ρwater⋅16A⋅23L⋅ρwater
- Simplifying this gives:
mmanmwood=1/62/3=16⋅32=14
Final Answer:
The ratio between the masses of the man and the wooden piece is 14.
- Let the length of the wooden cylinder be L.
- The volume of the wooden piece that is submerged when it is floating is 23L.
- The volume of the wooden piece can be expressed as Vwood=A⋅L, where A is the cross-sectional area.
- The weight of the wooden piece is equal to the weight of the water displaced by the submerged portion.
- The volume of water displaced is Vdisplaced=A⋅23L.
- The weight of the displaced water is given by:
Wdisplaced=Volume×Density of water×g=A⋅23L⋅ρwater⋅g
- Therefore, the weight of the wooden piece is:
Wwood=mwood⋅g=A⋅23L⋅ρwater⋅g
- When the man stands on the wooden piece, an additional 16L of the cylinder is submerged.
- The total submerged length now is 23L+16L=46L+16L=56L.
- The volume of water displaced now is:
Vdisplaced new=A⋅56L
- The weight of the displaced water is now:
Wdisplaced new=A⋅56L⋅ρwater⋅g
- The total weight when the man is standing on the wooden piece is the weight of the wooden piece plus the weight of the man:
mwood⋅g+mman⋅g=A⋅56L⋅ρwater⋅g
- Dividing through by g gives:
mwood+mman=A⋅56L⋅ρwater
- From the first condition, we have:
mwood=A⋅23L⋅ρwater
- Substitute mwood into the equation from step 4:
A⋅23L⋅ρwater+mman=A⋅56L⋅ρwater
- Rearranging gives:
mman=A⋅56L⋅ρwater−A⋅23L⋅ρwater
- Converting 23 to a fraction with a denominator of 6:
23=46
- Thus, we have:
mman=A⋅L⋅ρwater(56−46)=A⋅L⋅ρwater⋅16
- Now we can find the ratio of the mass of the man to the mass of the wooden piece:
mmanmwood=A⋅L⋅ρwater⋅16A⋅23L⋅ρwater
- Simplifying this gives:
mmanmwood=1/62/3=16⋅32=14
The ratio between the masses of the man and the wooden piece is 14.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Multipe Correct15videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Assertion-Reasoning8videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Subjective25videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE1videos
GRAVITATION
Similar Questions
A wooden block floats in water with two-third of its volume submerged.
When the same block is placed in oil, three quarters of its volume is immersed in oil. Calculate the density of oil.View SolutionA piece of wood floats in water with two-thirds of its volume submerged in water. In a certain oil it has 0.95 of its volume submerged. What is the density of wood and the oll?
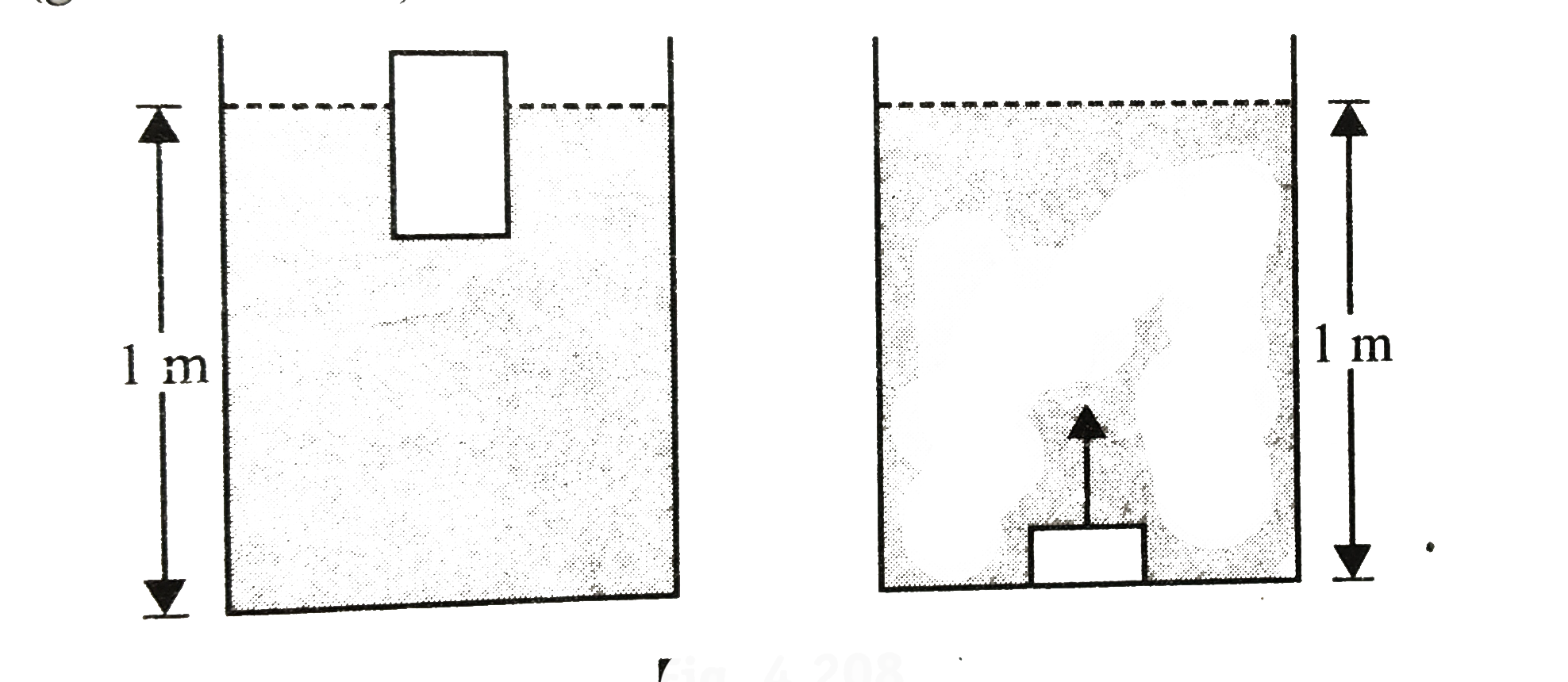
View SolutionA wooden block in the form of a uniform cylinder floats with one-third length above the water surface. A small chip of this block is held at rest at the bottom of a container containing water to a height of 1m and is then released. The time in which it will rise to the surface of water is =10m/s2)
 View Solution
View SolutionA wooden block floats in water with two third of its volume submerged. A. Calculate the density of wood.b. When the same block is placed in oil, three - quarter of its volume in immersed in oil. Calculate the density of oil.
View SolutionA body floats in water with its one-third volume above the surface. The same body floats in a liquid with one-third volume immersed. The density of the liquid is
View SolutionTwo solids A and B floats in water. It is observed that A floats with half of its volume immersed and B Floats with 2/3 of its volume immersed. The ratio of densities of A and B is
View SolutionA body P floats in water with half its volume immersed. Another body Q floats in a liquid of density 34th of the density of water with two - third of the volume immersed. The ratio of density of P to that of Q is
View SolutionA hollow cylindrical container floats in water with half its length immersed. A liquid of specific gravity σ is slowly poured into the container until the levels of the liquid inside the container and of water outside are the same. It is observed that the container is submerged to two-thirds its length. Then the value of σ is
View SolutionA uniform chain of mass m and length l is lying on a horizontal table with one-third of its length hanging over the edge of the table.

What is the speed of the chain, when it just loses contact with the table?View SolutionA uniform cube of mass M is floating on the surface of a liquid with three fourth of its volume immersed in the liquid (density=ρ). The length of the side of the cube is equal to
 View Solution
View Solution

