A metal ring of mass m and radius R is placed on a smooth horizontal table and is set rotating about its own axis in such a way that each part of the ring moves with a speed v. Find the tension in the ring.
To find the tension in a rotating metal ring of mass m and radius R, we can follow these steps:
1. Understanding the System:
- We have a metal ring of mass m and radius R that is rotating about its own axis. Each part of the ring moves with a speed v.
2. Angular Velocity:
- The angular velocity ω of the ring can be expressed as:
ω=vR
3. Consider a Small Element:
- Take a small element of the ring, dm, which subtends a small angle dθ at the center of the ring. The length of this small arc is:
dl=Rdθ
- The mass of this small element can be expressed as:
dm=m2πR⋅Rdθ=m2πdθ
- Here, m2πR is the mass per unit length of the ring.
4. Tension in the Ring:
- The tension T in the ring acts tangentially. For the small element dm, the tension acts inward and has components that can be resolved.
- The net inward force (centripetal force) required to keep the small mass dm moving in a circular path is given by:
FR=dm⋅v2R
5. Resolving Tension Forces:
- The tension in the ring contributes to the centripetal force. The components of the tension acting towards the center can be expressed as:
FR=2Tsin(dθ2)
- For small angles, we can approximate sin(dθ2)≈dθ2.
6. Setting Up the Equation:
- Equating the centripetal force to the tension components gives:
2T⋅dθ2=dm⋅v2R
- Substituting dm:
Tdθ=(m2π)⋅v2R
7. Cancelling dθ:
- Rearranging gives:
T=mv22πR
Final Result:
The tension in the ring is:
T=mv22πR
- We have a metal ring of mass m and radius R that is rotating about its own axis. Each part of the ring moves with a speed v.
- The angular velocity ω of the ring can be expressed as:
ω=vR
- Take a small element of the ring, dm, which subtends a small angle dθ at the center of the ring. The length of this small arc is:
dl=Rdθ
- The mass of this small element can be expressed as:
dm=m2πR⋅Rdθ=m2πdθ
- Here, m2πR is the mass per unit length of the ring.
- The tension T in the ring acts tangentially. For the small element dm, the tension acts inward and has components that can be resolved.
- The net inward force (centripetal force) required to keep the small mass dm moving in a circular path is given by:
FR=dm⋅v2R
- The tension in the ring contributes to the centripetal force. The components of the tension acting towards the center can be expressed as:
FR=2Tsin(dθ2)
- For small angles, we can approximate sin(dθ2)≈dθ2.
- Equating the centripetal force to the tension components gives:
2T⋅dθ2=dm⋅v2R
- Substituting dm:
Tdθ=(m2π)⋅v2R
- Rearranging gives:
T=mv22πR
The tension in the ring is:
T=mv22πR
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.125videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.216videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer5videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
Similar Questions
A metal rign of mass m and radius R is placed on a smooth horizontal table and is set rotating abut its own axis in such a way that each part of the ring moves with a speed v. Find the tension in the ring.
View SolutionFor a uniform ring of mass M and radius R at its centre
View SolutionA ring of mass m and radius R is placed on a rough inclined plane so that it rolls without slipping . Match the following table.


 View Solution
View SolutionA ring of mass m and radius R is given a charge q. It is then rotated about its axis with angular velocity ω.Find
(iii)Magnetic moment of ring.View SolutionA smooth ring of mass m and radius R=1m is pulled at P with a constant acceleration a=4ms−2 on a horizontal surface such that the plane of the ring lies on the surface. Find the angular acceleration of the ring at the given position. (in rad/s2)
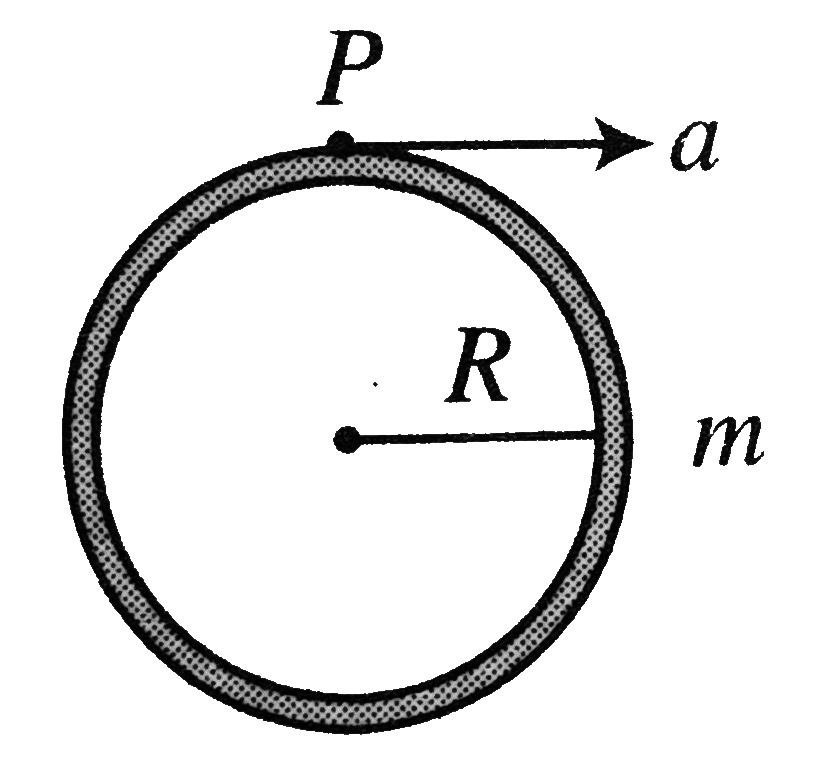 View Solution
View SolutionA small bead of mass m moving with velocity v gets threaded on a stationary semicircular ring of mass m and radius R kept on a horizontal table. The ring can freely rotate about its centre. The bead comes to rest relative to the ring. What will be the final angular velocity of the system?
 View Solution
View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be
 View Solution
View SolutionFrom a complete ring of mass M and radius R, a 30∘sector is removed. The moment of inertia of the incomplete ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is
 ,View Solution
,View Solution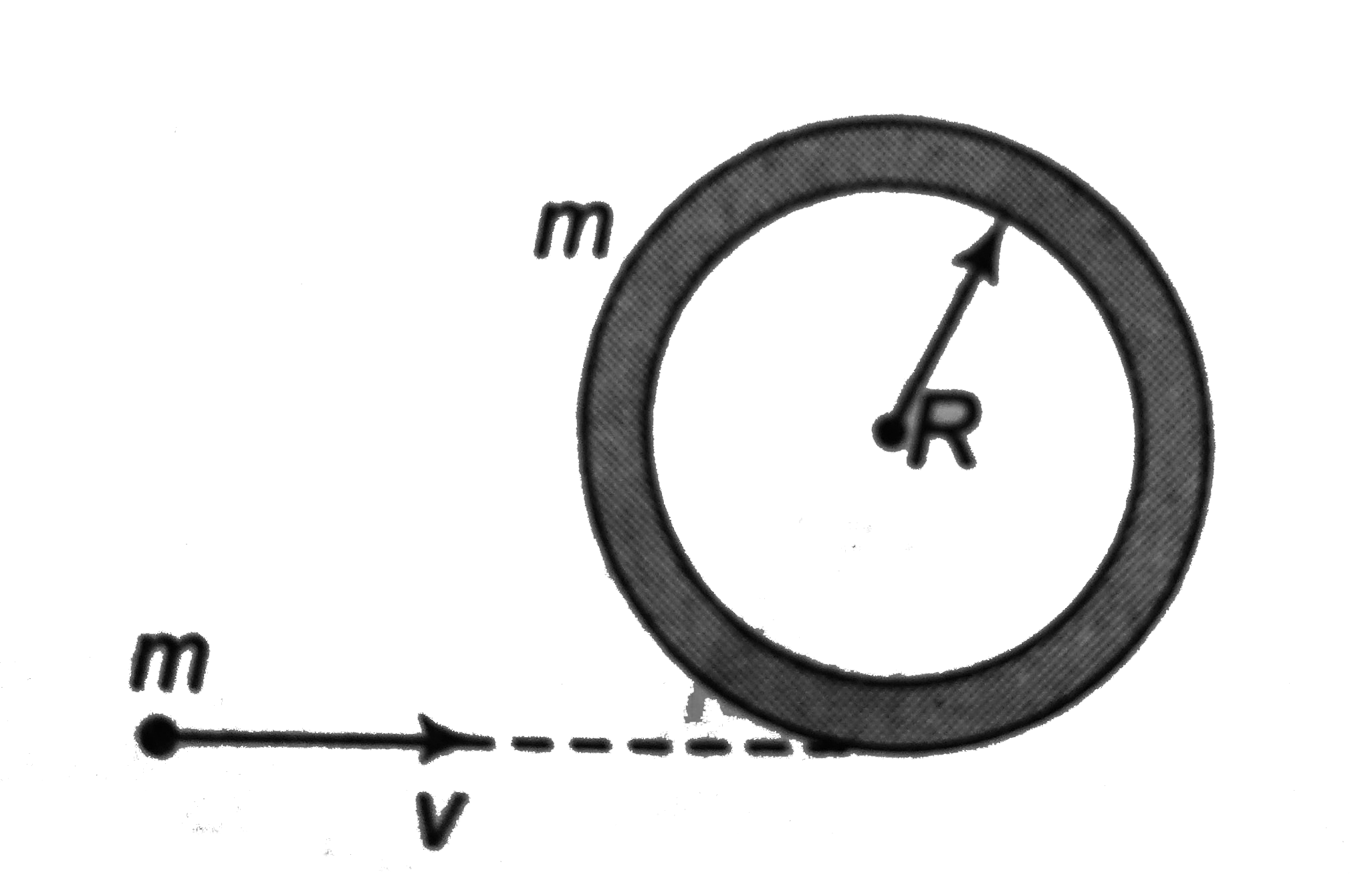
A circular ring of mass m and radius R rests flat on a horizontal smooth surface as shown in figure. A particle of mass m, and moving with a velocity v. Collides inelastically (e=0) with the ring the angular velocity with which the system rotates after the particle strikes the ring isView SolutionA ring of mass m and radius R is given a charge q. It is then rotated about its axis with angular velocity ω.Find
(i)Current produced due to motion of ringView Solution
