A metallic hemisphere is having dust on its surface. The sphere is rotated about a vertical axis passing through its centre at angular speed ω=10rads–1. Now the dust is visible only on top 20% area of the curved hemispherical surface. Radius of the hemisphere is R = 0.1 m. Find the coefficient of friction between the dust particle and the hemisphere [g=10ms–2].
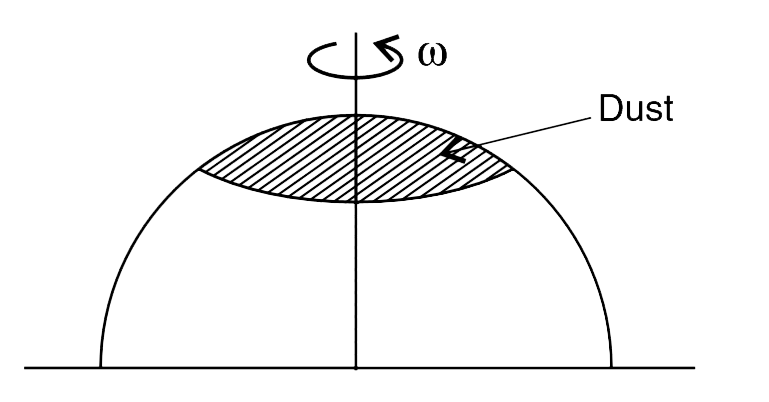
The correct Answer is:2.45
Step by step video, text & image solution for A metallic hemisphere is having dust on its surface. The sphere is rotated about a vertical axis passing through its centre at angular speed omega = 10 "rad" s^( –1). Now the dust is visible only on top 20% area of the curved hemispherical surface. Radius of the hemisphere is R = 0.1 m. Find the coefficient of friction between the dust particle and the hemisphere [g = 10 ms^(–2)]. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A particle is placed inside a hemispherical bowl which rotates about its vertical axis with constant angular speed ω. It is just prevented from sliding down when the line joining it to the centre of the hemisphere is 45∘ with the vertical. The radius of the bowl is 10√2m. The coefficient of friction between the particle and the bowl is 0.5 and g=10ms−2. Find the magnitude of ω.
View SolutionA metal disc of radius R can rotate about the vertical axis passing through its centre. The top surface of the disc is uniformly covered with dust particles. The disc is rotated with gradually increasing speed. At what value of the angular speed (ω) of the disc the 75%of the top surface will become dust free. Assume that the coefficient of friction between the dust particles and the metal disc is μ=0.5. Assume no interaction amongst the dust particles.
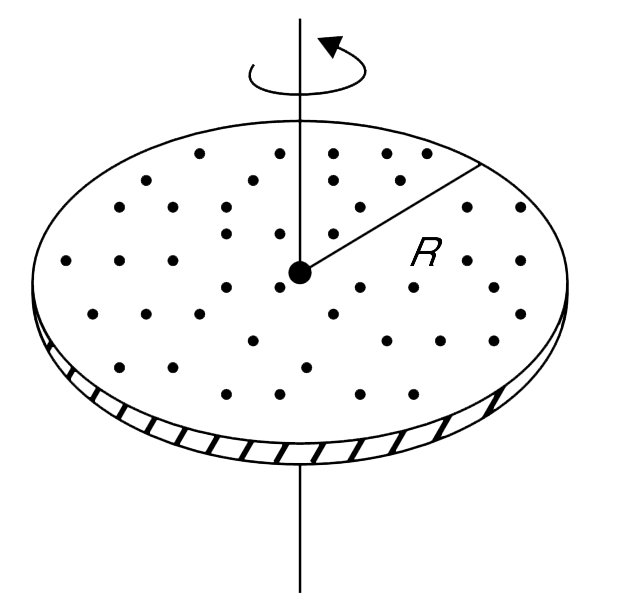
View Solution
Knowledge Check
A metal sphere of radius r and specific heat s is rotated about an axis passing through its centre at a speed of n rotations per second. It is suddenly stopped and 50% of its energy is used in increasing its temperature. The the rise in temperature of the sphere is
A2π2n2r25sB1π2n210r2sC78πr2n2sD5(πrn)214sA metal sphere of radius r and specific heat s is rotated about an axis passing through its centre at a speed of n rotations per second. It is suddenly stopped and 50% of its energy is used in increasing its temperature. The the rise in temperature of the sphere is
A2π2n2r25sB1π2n210r2sC78πr2n2sD5(πrn)214sA uniform disc of mass M and radius R is rotating about a horizontal axis passing through its centre with angular velocity ω . A piece of mass m breaks from the disc and flies off vertically upwards. The angular speed of the disc will be
A(M−2m)ω(M−m)B(M+2m)ω(M+m)C(M−2m)ω(M+m)D(M+2m)ω(M−m)
A metal sphere of radius R and specific heat C is rotated about an axis passing through its centre at a speed n rotation/second. It is suddenly stopped and 50% of its energy is used in increasing its temperature, then find the rise in temperature of the sphere
View SolutionA coin is placed at the edge of a horizontal disc rotating about a vertical axis through its axis with a uniform angular speed 2 rad s−1. The radius of the disc is 50 cm. Find the minimum coefficient of friction between disc and coin so that the coin does not slip. (Take g=10m/s2)
View SolutionA particle of mass m is placed over a horizontal circular table rotating with an angular velocity ω about a vertical axis passing through its centre. The distance of the object from the axis is r. Find the force of friction f between the particle and the table.
View SolutionA uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity ω. A particle of same mass m and having velocity of 2ωR towards centre of the disc collides with the disc moving horizontally and sticks to its rim. Then
View SolutionA uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity ω. A particle of same angular velocity mass m and moving horizontally with velocity 2ωR towards centre of the disc collides and sticks to its rim. The impulse on the particle due to the disc is
View Solution
