A metallic sphere of radius 18 cm has been given a charge of 5×10−6C. The energy of the charged conductor is
0.2J
0.6J
1.2J
2.4J
The correct Answer is:B
To find the energy of a charged metallic sphere, we can follow these steps:
Step 1: Identify the given values
- Radius of the sphere, R=18cm=0.18m
- Charge on the sphere, Q=5×10−6C
Step 2: Calculate the capacitance of the sphere
The formula for the capacitance C of a metallic sphere is given by:
C=4πϵ0R
where ϵ0 (the permittivity of free space) is approximately 8.85×10−12F/m.
Substituting the values:
C=4π(8.85×10−12)(0.18)
Calculating C:
C≈4×3.14×8.85×10−12×0.18
C≈2.00×10−12F
Step 3: Calculate the energy stored in the sphere
The energy U stored in a capacitor is given by the formula:
U=12CV2
We also know that V (the potential) can be expressed in terms of charge and capacitance:
V=QC
Substituting this into the energy formula gives:
U=12C(QC)2=12Q2C
Step 4: Substitute the values into the energy formula
Now substituting Q=5×10−6C and C≈2.00×10−12F:
U=12(5×10−6)22.00×10−12
Calculating U:
U=1225×10−122.00×10−12=12×12.5=6.25J
Final Answer
The energy of the charged conductor is approximately 6.25J.
---
- Radius of the sphere, R=18cm=0.18m
- Charge on the sphere, Q=5×10−6C
The formula for the capacitance C of a metallic sphere is given by:
C=4πϵ0R
where ϵ0 (the permittivity of free space) is approximately 8.85×10−12F/m.
C=4π(8.85×10−12)(0.18)
Calculating C:
C≈4×3.14×8.85×10−12×0.18
C≈2.00×10−12F
The energy U stored in a capacitor is given by the formula:
U=12CV2
We also know that V (the potential) can be expressed in terms of charge and capacitance:
V=QC
Substituting this into the energy formula gives:
U=12C(QC)2=12Q2C
Now substituting Q=5×10−6C and C≈2.00×10−12F:
U=12(5×10−6)22.00×10−12
Calculating U:
U=1225×10−122.00×10−12=12×12.5=6.25J
The energy of the charged conductor is approximately 6.25J.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - HOTS
5 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - EXEMPLAR PROBLEMS
3 Videos
- ELECTROMAGNETIC WAVESBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Assertion And Reason
15 Videos
- MAGNETISM AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - NCERT Exemplar
5 Videos
Similar Questions
A hollow metallic sphere of radius 10 cm is given a charge of 3.2×10−9C. The electric intensity at a point 4 cm from the center is
View SolutionTwo metallic spheres of radii 1cm and 2cm are given charges 10−2C and 5×10−2C respectively. If they are connected by a conducting wire, the final charge on the smaller sphere is
View Solution
Knowledge Check
A body has a positive charge of 8×10−19C. It has :
Aan excess of 5 electronsBa deficiency of 5 electronsCan excess of 8 electronsDa deficiency of 8 electrons
A hollow sphere of radius 0.1 m has a charge of 5×10−8C. The potential at a distance of 5 cm from the centre of the sphere is
(14πε0=9×109Nm2C−2)
View SolutionTwo isolated metallic spheres of radii 2 cm and 4 cm are given equal charge, then the ratio of charge density on the surfaces of the spheres will be
View SolutionA conducting sphere of radius r has a charge . Then .
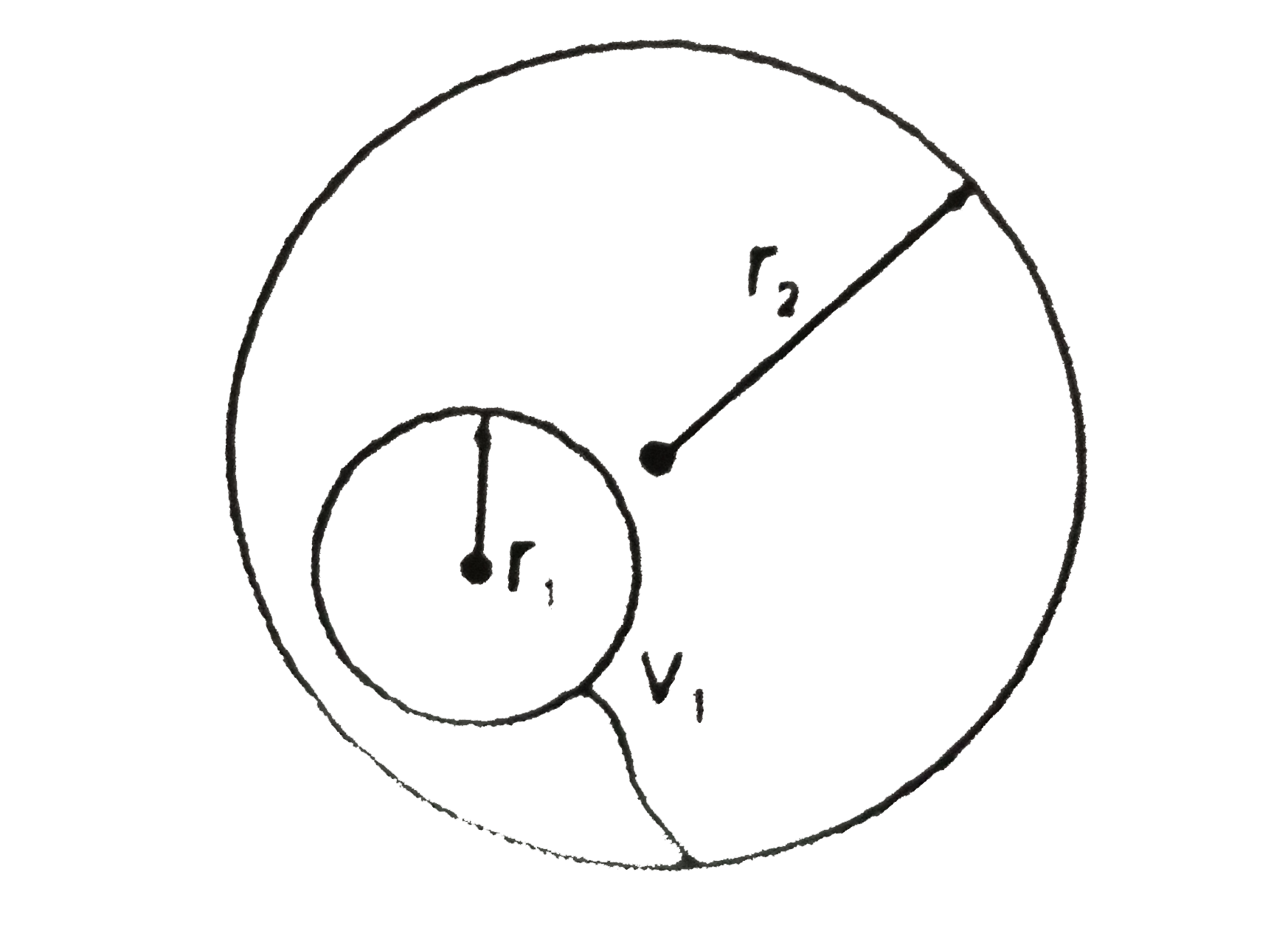
View SolutionA metal sphere of radius r1 charges to a potential V1 is then placed in a thin-walled uncharged conducting spherical shell of radius r2. Determine the potential acquired by the spherical shell after it has been connected for a short time to the sphere by a conductor.
View SolutionA spherical conductor of radius 12 cm has a charge of 1.6×10−7C distributed uniformly on its surface. What is the electric field (a) inside the sphere (b) just outside the sphere (c ) at a point 18 cm from the center of the sphere ?
View SolutionTwo metal spheres of radii 0.01 m and 0.02 m are given a charge of 15 mC and 45 mC, respectively. They are then connected by a wire. The final charge on the first is …×10−3C.
View SolutionA hollow metallic sphere of radius 0.1 m is charged to a potential of 5 V. The potential at its centre is
View Solution
