A motor drives a body along a straight line with a constant force. The power P developed by the motor must vary with time t as
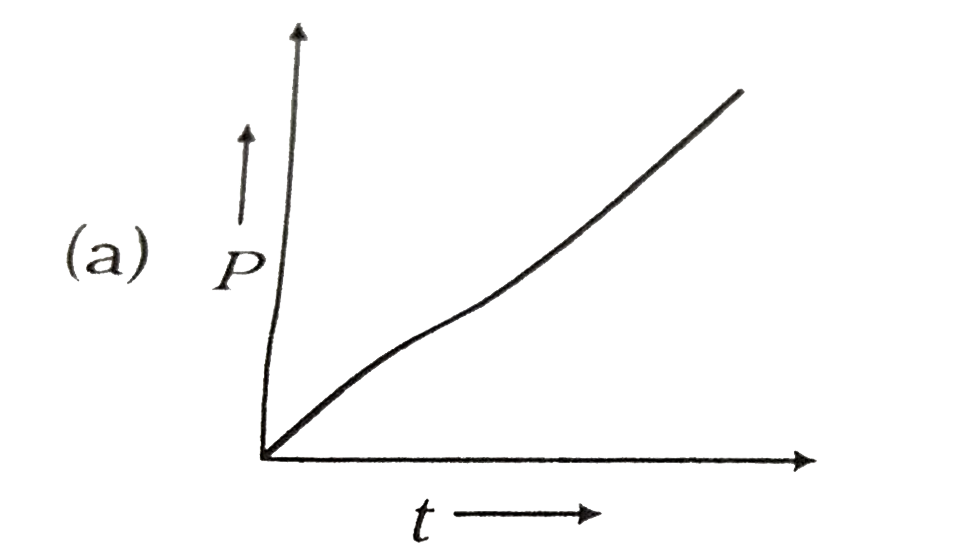

The correct Answer is:A
To solve the problem, we need to analyze the relationship between power, force, and velocity when a motor drives a body with a constant force. Here’s a step-by-step solution:
Step 1: Understand the relationship between force, mass, and acceleration
Given that the motor drives the body with a constant force F, we can express this using Newton's second law:
F=ma
where m is the mass of the body and a is its acceleration. Since the force is constant, the acceleration a must also be constant.
Step 2: Relate velocity to time
Using the equation of motion for uniformly accelerated motion, we have:
v=u+at
Assuming the initial velocity u=0 (the body starts from rest), this simplifies to:
v=at
This shows that the velocity v of the body increases linearly with time t since a is constant.
Step 3: Write the expression for power
The power P developed by the motor is given by the formula:
P=F⋅v
Substituting the expression for velocity from Step 2:
P=F⋅(at)
Since F is constant, we can rewrite this as:
P=(F⋅a)t
This indicates that power P is directly proportional to time t.
Step 4: Conclusion about the relationship
From the equation P=(F⋅a)t, we can conclude that as time increases, power also increases linearly. Thus, we can express this relationship as:
P∝t
Step 5: Identify the correct graph
Since power varies linearly with time, the graph of power P versus time t will be a straight line passing through the origin.
Final Answer
The power P developed by the motor varies with time t as:
P∝t
The correct option is that the graph of power versus time is a straight line passing through the origin.
---
Given that the motor drives the body with a constant force F, we can express this using Newton's second law:
F=ma
where m is the mass of the body and a is its acceleration. Since the force is constant, the acceleration a must also be constant.
Using the equation of motion for uniformly accelerated motion, we have:
v=u+at
Assuming the initial velocity u=0 (the body starts from rest), this simplifies to:
v=at
This shows that the velocity v of the body increases linearly with time t since a is constant.
The power P developed by the motor is given by the formula:
P=F⋅v
Substituting the expression for velocity from Step 2:
P=F⋅(at)
Since F is constant, we can rewrite this as:
P=(F⋅a)t
This indicates that power P is directly proportional to time t.
From the equation P=(F⋅a)t, we can conclude that as time increases, power also increases linearly. Thus, we can express this relationship as:
P∝t
Since power varies linearly with time, the graph of power P versus time t will be a straight line passing through the origin.
The power P developed by the motor varies with time t as:
P∝t
The correct option is that the graph of power versus time is a straight line passing through the origin.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRANCE SPECIAL QUESTIONS
16 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MATCH THE COLUMNS
7 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - CHECK POINT 6.3
10 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - E Integer Type Questions
11 Videos
Similar Questions
A machine is delivering constant power to drive a body along a straight line. What is the relation between the distance travelled by the body against time ?
View SolutionA body moves under the action of a constant force along a straight line. The instantaneous power developed by this force with time t is correctly represented by.
View SolutionA body is moved along a straight line by a machine delivering constant power . The distance moved by the body is time t is proptional to
View SolutionA body is moved along a straight line by a machine delivering constant power . The distance moved by the body is time t is proptional to
View SolutionA body is moved along a straight line by a machine delivering constant power . The distance moved by the body is time t is proptional to
View SolutionThe power supplied by a force acting on a particle moving in a straight line is constant. The velocity of the particle varies with the displacement x as :
View SolutionThe power supplied by a force acting on a particle moving in a straight line is constant. The velocity of the particle varies with displacement as x1K. Find the value of K.
View SolutionA body starting from rest moves along a straight line with a constant acceleration. The variation of speed (v) with distance (s) is represented by the graph:
View SolutionThe position - time graph for a particle moving along a straight line is shown in figure. The total distance travelled by it in time t = 0 to t = 10 s is
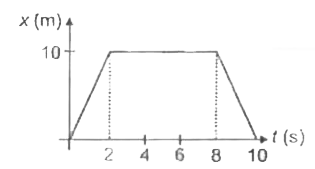
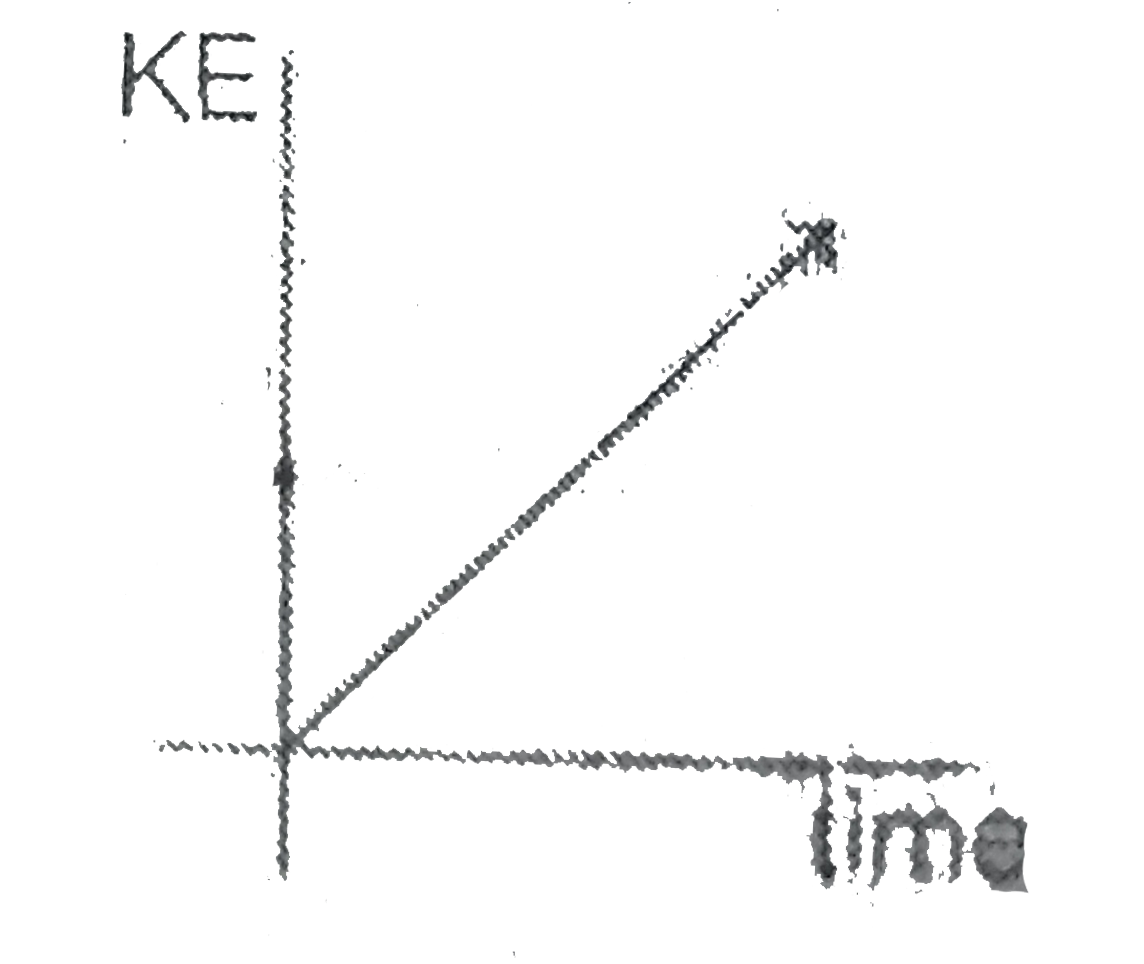
View SolutionThe kinetic energy (KE) versus time graph for a particle moving along a straight line is as shown in the figure. The force versus time graph for the particle may be
View Solution
