A motorcycle is going on an overbridge of radius R. The driver maintains a constant speed. As the motorcycle is ascending on the overbridge, the normal force on it
increase
decrease
remains the same
fluctuates
The correct Answer is:A
To solve the problem regarding the normal force acting on a motorcycle ascending an overbridge of radius R while maintaining a constant speed, we can follow these steps:
1. Understanding Forces Acting on the Motorcycle:
- When the motorcycle is on the overbridge, two main forces act on it: the gravitational force (mg) acting downward and the normal force (N) acting perpendicular to the surface of the bridge.
2. Identifying the Components of Forces:
- As the motorcycle ascends, we can break down the gravitational force into two components:
- One component acting towards the center of the circular path: mgcosθ
- The other component acting perpendicular to the surface: mgsinθ
3. Applying Newton's Second Law:
- For circular motion, the net centripetal force required to keep the motorcycle moving in a circle is given by:
Fcentripetal=mv2R
- The net force towards the center of the circle can be expressed as:
mgcosθ−N=mv2R
- Rearranging this gives us the equation for the normal force:
N=mgcosθ−mv2R
4. Analyzing the Change in Normal Force:
- As the motorcycle ascends the overbridge, the angle θ decreases. This means that cosθ increases because cosine is a decreasing function in the range of 0 to 90 degrees.
- Since the speed v is constant, the term mv2R remains constant.
5. Conclusion on Normal Force:
- As cosθ increases, the term mgcosθ increases, leading to an increase in the normal force N.
- Therefore, the normal force acting on the motorcycle increases as it ascends the overbridge.
Final Answer:
The normal force on the motorcycle increases as it ascends the overbridge.
---
- When the motorcycle is on the overbridge, two main forces act on it: the gravitational force (mg) acting downward and the normal force (N) acting perpendicular to the surface of the bridge.
- As the motorcycle ascends, we can break down the gravitational force into two components:
- One component acting towards the center of the circular path: mgcosθ
- The other component acting perpendicular to the surface: mgsinθ
- For circular motion, the net centripetal force required to keep the motorcycle moving in a circle is given by:
Fcentripetal=mv2R
- The net force towards the center of the circle can be expressed as:
mgcosθ−N=mv2R
- Rearranging this gives us the equation for the normal force:
N=mgcosθ−mv2R
- As the motorcycle ascends the overbridge, the angle θ decreases. This means that cosθ increases because cosine is a decreasing function in the range of 0 to 90 degrees.
- Since the speed v is constant, the term mv2R remains constant.
- As cosθ increases, the term mgcosθ increases, leading to an increase in the normal force N.
- Therefore, the normal force acting on the motorcycle increases as it ascends the overbridge.
The normal force on the motorcycle increases as it ascends the overbridge.
Topper's Solved these Questions
- CIRCULAR MOTIONBook:HC VERMA ENGLISHChapter:CIRCULAR MOTIONExercise:Objective -2
Explore 6 Videos
- CIRCULAR MOTIONBook:HC VERMA ENGLISHChapter:CIRCULAR MOTIONExercise:Exercises
Explore 30 Videos
- CIRCULAR MOTIONBook:HC VERMA ENGLISHChapter:CIRCULAR MOTIONExercise:worked out Examples
Explore 13 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBook:HC VERMA ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONExercise:Objective -2
Explore 11 Videos
- FLUID MECHANICSBook:HC VERMA ENGLISHChapter:FLUID MECHANICSExercise:All Questions
Explore 90 Videos
Similar Questions
Knowledge Check
A body of mass m is moving in a circle of radius r with a constant speed v. The work done by the centripetal force in moving the body over half the circumference of the circle is
Amv2/rBzeroCmv2/rDr2/mv2A particle is moving on a circular path of radius R with constant speed v. During motion of the particle form point A to point B
 AAverage speed is v/2BThe magnitude of average velocity is v/πCThe magnitude of average acceleration is 2v2πRDAverage velocity is zero.
AAverage speed is v/2BThe magnitude of average velocity is v/πCThe magnitude of average acceleration is 2v2πRDAverage velocity is zero.
A car is going round a circle of radius R1 with constant speed. Another car is going round a circle of radius R2 with constant speed. If both of them take same time to complete the circles, the ratio of their angular speeds and linear speeds will be
View SolutionA particle is moving in a circle of radius R with constant speed. The time period of the particle is T. In a time t=T6
Average velocity of the particle is…..
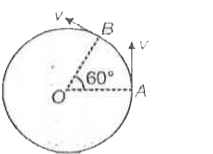
View SolutionA particle is moving in a circle of radius r having centre at O with a constant speed v . The magnitude of change in velocity in moving from A to B is
View SolutionA body of mass m is moving in a circle of radius r with a constant speed v, The force on the body is mv2r and is directed towards the centre what is the work done by the from in moving the body over half the circumference of the circle?
View SolutionA train of mass M is moving on a circular track of radius R with constant speed v. The length of the train is half of the perimeter of the track. The linear momentum of the train will be
View SolutionA train of mass M is moving on a circular track of radius R with constant speed v. The length of the train is half of the perimeter of the track. The linear momentum of the train will be
View Solution