A non-deformed spring whose ends are fixed has a stiffness $x = 13 N / m$ . A small body of mass $m = 25 g$ is attached at the point removed from one of the ends by $η = 1 / 3$ of the spring's length. Neglecting the mass of the spring, find the period of small longitudinal oscillations of the body. The force of gravity is assumed to be absent.

Video Solution

Text Solution

Verified by Experts

At first let us calculate the stiffness $k_{1}$ and $k_{2}$ of both the parts of the spring. If we subject the original spring of stiffness $k$ having the natural length $l_{0}$ (say), under the deforming forces $F - F$ (say) to elongate the spring by the amount $x$ , then
$F = k x ... . (1)$
Therefore the elongation per unit length of the spring is $x / l_{0}$ . Now let us subject one of the parts of the spring of natural length $η l_{0}$ under the same deforming forces $F - F$ . Then the elongation of the spring will be
$\frac{x}{l_{0}} η l_{0} = η x$
Thus $F = k_{1} (η x) ... . (2)$
Hence from Eqns $(1)$ and $(2)$
$k = η k_{1}$ or $k_{1} = k / η ... . (3)$
Similarly $k_{2} = \frac{k}{1 - η}$
The position of the block $m$ when both the parts of the spring are non- deformed, is its equilibrium position $O$ . Let us displace the block $m$ towards right or in positive $x$ axis by the small distance $x$ . Let us depict the forces acting on the block when it is at a distance $x$ from its equilibrium position (figure). From the second law of motion in projection form $i . e ., F_{x} = m w_{x}$
$- k_{1} x - k_{2} x = m .. x$
or, $- (\frac{k}{η} + \frac{k}{1 - η}) x = m .. x$
Thus $.. x = - \frac{k}{m} \frac{1}{η (m)} x$
Hence the sought time period
$T = 2 π \sqrt{η (1 - n) m / k} = 0.13 s$

Updated on:21/07/2023

On a smooth inclined plane, a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has force constant K , the period of oscillation of the body (assuming the springs as massless) is
A $2 π {(\frac{m}{2 K})}^{1 / 2}$
B $2 π {(\frac{2 M}{K})}^{1 / 2}$
C $2 π \frac{M g sin θ}{2 K}$
D $2 π {(\frac{2 M g}{K})}^{1 / 2}$
On a smooth inclined plane a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has a force constant k, the period of oscilation of the body is (assuming the spring as massless)

A $2 π \sqrt{\frac{M}{2 k}}$
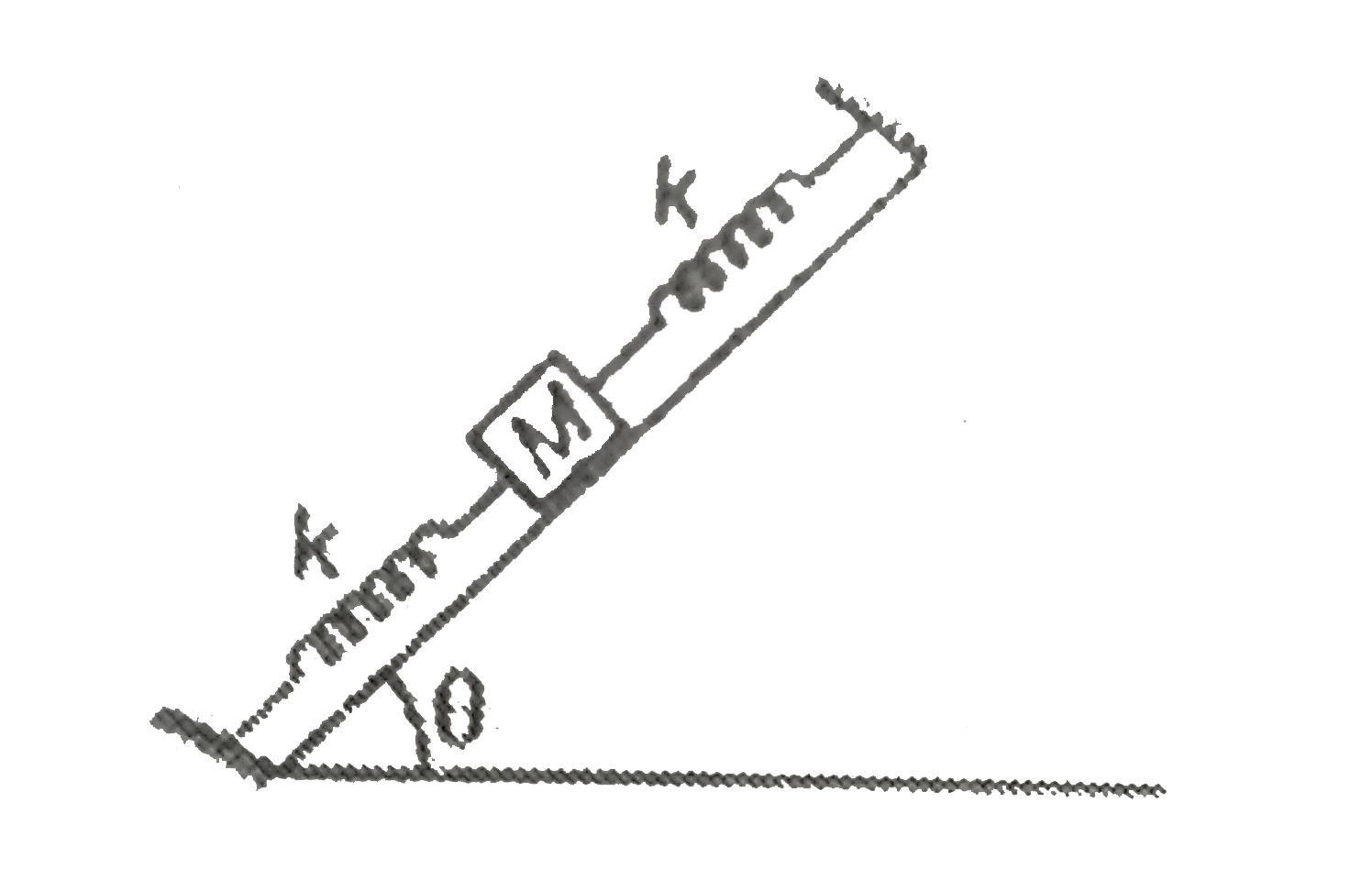B $2 π \frac{\sqrt{2 M}}{k})$
C $2 π \frac{\sqrt{M sin θ}}{2 k}$
D $2 π \frac{\sqrt{2 M sin θ}}{k})$
On a smooth inclined plane a body of mass M is attached between two springs. The other ends of the spring are fixed to ffirm supports. If each spring has a force constant k, the period of oscillation of the body is: (assuming the spring as massless)

A $2 π \sqrt{\frac{M}{2 K}}$
B $2 π \sqrt{\frac{2 M}{K}}$
C $2 π \sqrt{\frac{M Sin θ}{K}}$
D $2 π \sqrt{\frac{2 M Sin θ}{K}}$