(a) Obtain the expression for the magnetic energy stored in a solenoid in terms of magnetic field B, area A and length l of the solenoid. (b) How does this magnetic energy compare with the electrostatic energy stored in a capacitor?
(a) From Eq. (6.19), the magnetic energy is
UB=12LI2
=12L(Bμ0n)2 (since B=μ0ni, for a solenoid)
12(μ0n2Al)(Bμ0n)2 [From Eq. (6.17)]
=12μ0B2Al
(b) The magnetic energy per unit volume is,
ub=UBV (where V is volume that contains flux)
=UBAl
=B22μ0
We have already obtained the relation for the electrostatic energy stored per unit volume in a parallel plate capacitor (refer to Chapter 2, Eq. 2.77),
uE=12ε0E2
In both the cases energy is proportional to the square of the field strength. Equations (6.20) and (2.77) have been derived for special cases: a solenoid and a parallel plate capacitor, respectively. But they are general and valid for any region of space in which a magnetic field or/and an electric field exist.
Topper's Solved these Questions
- BOOK - NCERT ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise17videos
ELECTROMAGNETIC INDUCTION
- BOOK - NCERT ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Exercise34videos
ELECTRIC CHARGES AND FIELDS
- BOOK - NCERT ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise15videos
ELECTROMAGNETIC WAVES
Similar Questions
Derive the expression for the magnetic energy stored in a solenoid in terms of magnetic field B, area A and length l of the solenoid carrying a steady current 1. How does this magnetic energy per unit volume compare with the electrostatic energy density stored in a parallel plate capacitor ?
View SolutionThe total electrostatic energy stored in both the capacitor is
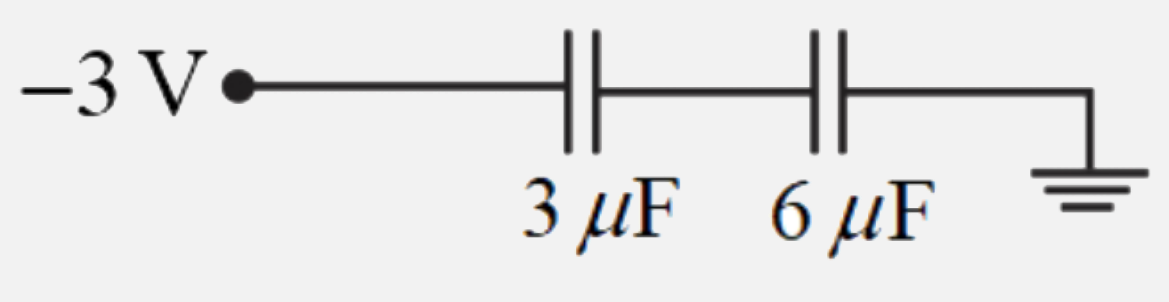 View Solution
View SolutionIn the figure magnetic energy stored in the coil is
 View Solution
View SolutionStrating from the expression for the energy W=12LI2, stored in a solenoid of self-inductance L to build up the current I, obtain the expression for the magnetic energy in terms of the magnetic field B, area A and length l, of the solenoid having n number of turns per unit length. Hence show that the energy density is given by B2/2μo.
View SolutionThe magnetic energy stored in a long solenoid of area of cross-section A in a small region of length L is
View SolutionThe total electrostatic energy stored in both the capacitors (in μJ) is
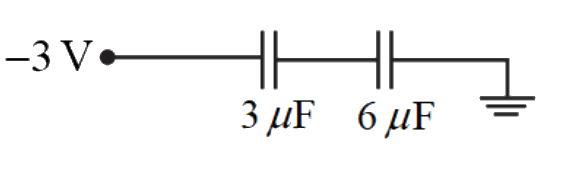 View Solution
View SolutionDeduce an expression for the potential energy stored in a parallel plate capacitor.
View SolutionA 12 pF capacitor is connected to a 50 V battery. How much electrostatic energy is stored in the capacitor ?
View SolutionThe expression for magnetic induction inside a solenoid of length L carrying a current I and having N number of turns is
View SolutionThe magnetic field along the axis of an air cored solenoid is B. The magnetic field energy density is
View Solution

