A pan of mass and a block of mass are connected to each other by a light inextensible string, passing over a light pulley as shown in Fig. Initially, the block is resting on a horizontal floor. A ball of mass collides with the pan at a speed . Consider this instant of collision as . Assume collision to be perfectly inelastic. Now, Fig. answer the following questions based on the above information.

Find the velocity of pan + ball system at . Assume that the block comes to rest instantaneously after striking the floor.
downward
upward
upward
downward
The correct Answer is:D
Due to collision an impulsive tension occurs in the string.
For ball pan system
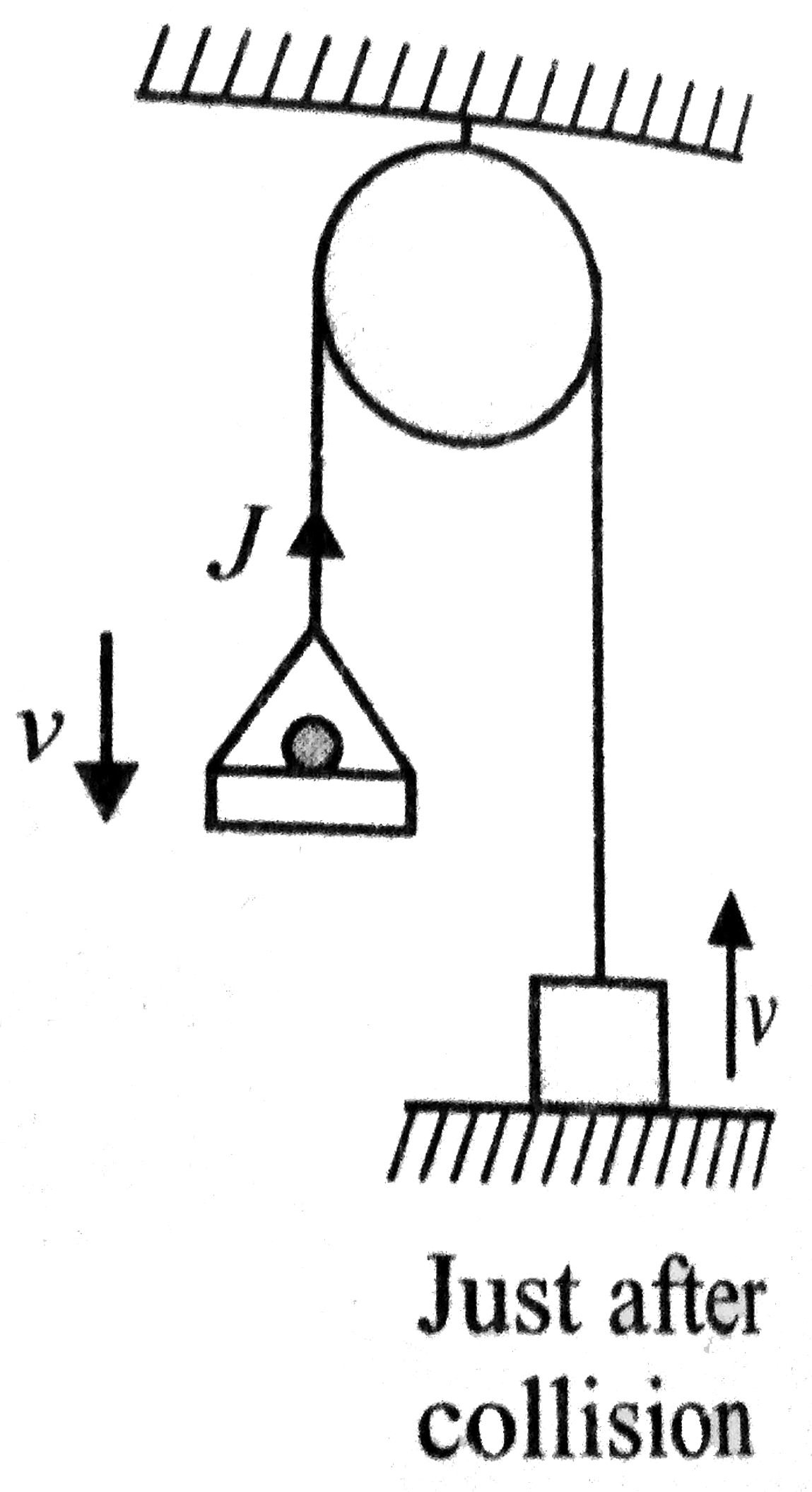
For block
As the string is taut and the mass of the block is greater than the mass of ball pan, so the block and ball pan are under deceleration given by
So, block will again come to ground after time , given by
At this instant, the pan ball system is moving with and the stirng gets slacked, so the system is moving under gravity.
To determine the speed of the system at , first find the time after which string is again jerked. that will happen when pan ball system crosses its instant during its downward journey, i.e., after its time of flight of motion under gravity.
i.e., string will again jerk at
For , the system is again under a retardation of . Before this, find the velocity of various component of system just after jerk.
We have
and
(downward)
The maximum height attained by theh block after the second jerk is given by
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Integer
16 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Fill In The Blanks
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A bullet is fired on a fixed target. It penetrates inside the target through distance d=3.75cm and then stops. mass of the bullet is m=1kg and of the target is M=4kg. Now an identical bullet moving with the same velocity is fired on the identical target which is placed at rest on a frictionless horizontal surface. Then find the distance (in cm) to which the bullet will penetrate inside the target?
View SolutionA particle of mass 4 m which is at rest explodes into three fragments. Two of the fragments each of mass m are found to move with a speed v each in mutually perpendicular directions. The total energy released in the process of explosion is ............
View SolutionStatement I: In a two-body collision, the momenta of the particles are equal and opposite to one another, before as well as after the collision when measured in the centre of mass frame.
Statement. II: The momentum of the system is zero from the centre of mass frame.
View SolutionA colorimeter contains 400g of water at a temperature of 5∘C. Then, 200g of water at a temperature of +10∘C and 400g of ice at a temperature of −60∘C are added. What is the final temperature of the contents of calorimeter?
Specific heat capacity of water −1000 cal/kg/K
Specific latent heat of fusion of ice =80×1000 cal/kg
Relative specific heat of ice =0.5
View SolutionTo find the distance d over which a signal can be seen clearly in foggy conditions, a railways-engineer uses dimensions and assumes that the distance depends on the mass density ρ of the fog, intensity (power/area) S of the light from the signal and its frequency f. the engineer finds that d is proportional to S1/n. the value of n is
View SolutionA block of mass m and α pan of equla mass are connected by a string going over a smooth light pulley as shwon in figure. Initially the systemis at rest when a particle of mass m falls on the pan and sticks to it. If the particle strikes thepan witha speed v find the speed with which the system moves just after the collision.
View SolutionA pan of mass m = 1.5 kg and a block of mass M = 3 kg are connected to each other by a light inextensible string, passing over a light pulley as shown in Fig. Initially, the block is resting on a horizontal floor. A ball of mass m_0 = 0.5 kg collides with the pan at a speed v_0= 20 m//s . Consider this instant of collision as t = 0 . Assume collision to be perfectly inelastic. Now, Fig. answer the following questions based on the above information. Mark the correct statement(s) for this situation
View SolutionA pan of mass m = 1.5 kg and a block of mass M = 3 kg are connected to each other by a light inextensible string, passing over a light pulley as shown in Fig. Initially, the block is resting on a horizontal floor. A ball of mass m_0 = 0.5 kg collides with the pan at a speed v_0= 20 m//s . Consider this instant of collision as t = 0 . Assume collision to be perfectly inelastic. Now, Fig. answer the following questions based on the above information. Find the time t at which the block strikes the floor for the first time
View SolutionA pan of mass m=1.5kg and a block of mass M=3kg are connected to each other by a light inextensible string, passing over a light pulley as shown in Fig. Initially, the block is resting on a horizontal floor. A ball of mass m0=0.5kg collides with the pan at a speed v0=20m/s. Consider this instant of collision as t=0. Assume collision to be perfectly inelastic. Now, Fig. answer the following questions based on the above information.

. Find the maximum height reached by the block alter the second jerk.
View SolutionTwo blocks A and B , each of mass 10 kg , are connected by a light string passing over a smooth pulley as shown in the figure. Block A will remain at rest if the friction on it is
View SolutionA block of mass M is placed on a rough horizontal surface. It is connected by means of a light inextensible string passing over a smooth pulley . The other end of string is connected to a block of mass m. There is no friction between vertical surface and block m
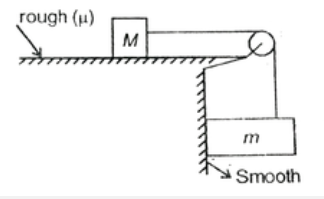
The minimum value of coefficient of friction μ such that system remains at rest , is
View Solutionचाल 5 मी/से से गतिमान द्रव्यमान 10 किग्रा का एक गुटका विरामावस्था में रखे द्रव्यमान 20 किग्रा के एक दूसरे गुटके से टकराता है तथा चाल 2 मी/से से वापस लौट आता है | टक्कर के उपरांत दूसरे गुटके का वेग क्या होगा ?
View SolutionTwo masses of 10 kg and 20 kg are connected with an inextensible string passing over two smooth pulleys as shown in the figure. The acceleration of 20 kg mass will be :
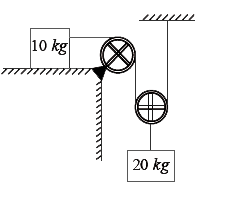
View SolutionA block of mass m_(1)=2 kg is kept on a smooth horizontal table. Another block of mass m_(2)=1 kg is connected to m_(1) by a light inextensible string passing over a smooth pulley as shown in the figure. If the blocks are released, what will be the (a) acceleration of each block (b) tension in the string?
View SolutionA block of mass m and a pan of equal mass are connected by a string going over a smooth light pulley as shown in figure. Initially the system is at rest when a particle of mass m falls on the pan and sticks to it. If the particle strikes the pan with a speed v find the speed with which the system moves just after the collision.
View Solution
