A parallel plate capacitor , each with plate area A and separation d , is charged to a potential difference V . The battery used to charge it remains connected . A dielectric slab of thickness of and dielectric constant K is now placed between the plates . What change , if any , will take place in :
charge on plates ?
Justify your answer
Given that plate area of either plate of parallel plate capacitor = A distance between the plates = d and potential difference between the plates = V
Hence initially capacitance C=∈0Ad and charge on plates Q = CV
As the battery remains connected throughout the potential difference between the plates remains unchanged (V. = V) On placing a dielectric slab of the thickness .d. and dielectric constant .K. between the plates
New capacitance of the capacitor C.=K∈0Ad=KC
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - LONG ANSWER QUESTIONS-II
13 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SELF ASSESSMENT TEST
1 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SHORT ANSWER QUESTIONS
48 Videos
- ELECTROMAGNETICE INDUCTIONBOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETICE INDUCTIONEXERCISE - Self Assessment Test Section -D
1 Videos
- EXAMINATION PAPER 2020 (SOLVED)BOOK - U-LIKE SERIESCHAPTER - EXAMINATION PAPER 2020 (SOLVED)EXERCISE - SECTION D
6 Videos
Similar Questions
A parallel plate capacitor , each with plate area A and separation d , is charged to a potential difference V . The battery used to charge it remains connected . A dielectric slab of thickness of and dielectric constant K is now placed between the plates . What change , if any , will take place in :
capacitance of the capacitor ? Justify your answer .
View SolutionA parallel plate capacitor , each with plate area A and separation d , is charged to a potential difference V . The battery used to charge it remains connected . A dielectric slab of thickness of and dielectric constant K is now placed between the plates . What change , if any , will take place in :
electric filed intensity between the plates ? Justify your answer .
View Solution
Knowledge Check
Separation between the plates of parallel plate capacitor is 5 mm. this capacitor, having air as the dielectric medium between the plates, is charged to a potential difference 25 V using a battery. The battery is then disconnected and a dielectric slab of thickness 3mm and dielectric constant K=10 is placed between the plates as shown. potential difference between the plates after the dielectric slab has been introduced is-
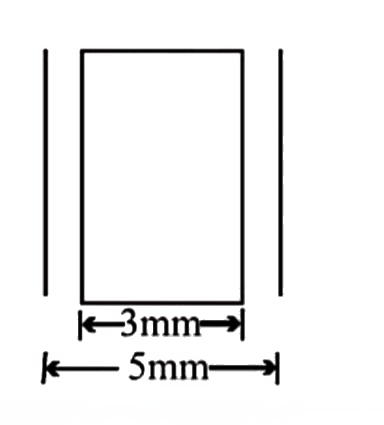 A18.5VB13.5VC11.5VD6.5V
A18.5VB13.5VC11.5VD6.5VA parallel plate capacitor of plate area A and plate separation d is charged to potential difference V and then the battery is disconnected. A slab of dielectric constant K is then inserted between the plates of the capacitor so as to fill the space between the plates. If Q, E and W denote respectively, the magnitude of charge on each plate, the electric field between the plates (after the slab is inserted), and work done on the system, in question, in the process of inserting the slab, then
A(a) Q=ε0AVdB(b) Q=ε0KAVdC(c) E=VKdD(d) W=ε0AV22d[1−1K]
A parallel plate capacitor each with plate area A and separation ‘d’ is charged to a potential difference V. The battery used to charge it is then disconnected. A dielectric slab of thickness d and dielectric constant K is now placed between the plates. What change if any, will take place in
(i) charge on the plates
(ii) electric field intensity between the plates,
(iii) capacitance of the capacitor
Justify your answer in each case
View SolutionA parallel plate capacitor each with plate area A and separation ‘d’ is charged to a potential difference V. The battery used to charge it is then disconnected. A dielectric slab of thickness d and dielectric constant K is now placed between the plates. What change if any, will take place in
(i) charge on the plates
(ii) electric field intensity between the plates,
(iii) capacitance of the capacitor
Justify your answer in each case
View SolutionA parallel plate capacitor has plates of area 0.080m2 and a separation of 1.2 cm . A battery charges the plates to a potential difference of 120V and is then disconnected . A dielectric slap of thickness 4.0mm and dielectric constant 4.8 is then placed symmetrically between the plates (a) What is the capacitance with the slab in place ? What is the free charge q (c) before and (d) after the slap is inserted ? What is the magnitude of the electric field (e) in the space between the plates and dielectric and (f) in the electric itself? (g) with the slab in place, what is the potential difference across teh plates (h) How much external work is involved in inserting the slab?
View SolutionSeparation between the plates of parallel plate capacitor is 5 mm. this capacitor, having air as the dielectric medium between the plates, is charged to a potential difference 25 V using a battery. The battery is then disconnected and a dielectric slab of thickness 3mm and dielectric constant K=10 is placed between the plates as shown. potential difference between the plates after the dielectric slab has been introduced is-

View SolutionA parallel - plate capacitor of plate area Aand plate separation d is charged to a potential difference V and then the battery is disconnected . A slab of dielectric constant K is then inserted between the plate of the capacitor so as to fill the space between the plate .Find the work done on the system in the process of inserting the slab.
View SolutionA parallel - plate capacitor of plate area A and plate separation d is charged to a potential difference V and then the battery is disconnected . A slab of dielectric constant K is then inserted between the plate of the capacitor so as to fill the space between the plate .Find the work done on the system in the process of inserting the slab.
View Solution
