Two parallel plate capacitors of capacitances C1 and C2 such that C2=2C1 are connected across battery of V volts as shown in the Fig . Initially the key K is kept closed to fully charge the capacitors . The key K is now thrown open and dielectric slabs of dielectric constant K0 are inserted in the two capacitors to completely fill the gap between the plates .

Find the ratio of the energies stored in the combination before and after the introduction of dielectric slabs .
Total initial energy of the combination Ui=12CiV2
As the key K is then thrown open , net charge Q remains constant but voltage V changes to Vf=VK0
∴ Total final energy of the combination Uf=12CfV2f=12(K0.Cf)(VK0)2=C1⋅V22K0⇒UiUf=K0
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - LONG ANSWER QUESTIONS-II
13 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SELF ASSESSMENT TEST
1 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SHORT ANSWER QUESTIONS
48 Videos
- ELECTROMAGNETICE INDUCTIONBOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETICE INDUCTIONEXERCISE - Self Assessment Test Section -D
1 Videos
- EXAMINATION PAPER 2020 (SOLVED)BOOK - U-LIKE SERIESCHAPTER - EXAMINATION PAPER 2020 (SOLVED)EXERCISE - SECTION D
6 Videos
Similar Questions
Two parallel plate capacitors of capacitances C1 and C2 such that C2=2C1 are connected across battery of V volts as shown in the Fig . Initially the key K is kept closed to fully charge the capacitors . The key K is now thrown open and dielectric slabs of dielectric constant K0 are inserted in the two capacitors to completely fill the gap between the plates .

Find the ratio of the net capacitance
View SolutionTwo dielectric slabs of dielectric constants K1andK2 are filled in between the two plates, each of area A, of the parallel plate capacitor as shown in the figure. Find the net capacitance of the capacitor.

View Solution
Knowledge Check
A parallel -plate air capacitor has capacity C. A dielectric slab of dielectric constant K, whose thickness is half of the air gap between the plates, is now inserted between the plates. The capacity of the capacitor will now be
AKC/2B2KC/(K+1)C2KC/(K−1)DC(K+1)/(K−1)
In the arrangement shown, the battery is disconnected and a dielectric slab of dielectric constant K is insereted between the plates of capacitor with capacitance C, so as to completely fill the space. What is the final potential differnece across capacitor with capacitance 2C ?
View SolutionTwo parallel plate capacitors of capacitances C and 2C are connected in parallel and charged to a potential difference V. The battery is then disconnected and the region between the plates of the capacitor C is completely filled with a material of dielectric constant K. The potential differences across the capacitors now becomes...........
View SolutionTwo parallel plate capacitors of capacitances C and 2C are connected in parallel and charged to a potential difference V. The battery is then disconnected and the region between the plates of the capacitor C is completely filled with a material of dielectric constant K. The potential differences across the capacitors now becomes...........
View SolutionFigure shows two idential capacitors, C1andC2, each of 1μF capacitance connected to a battery of 6 V. Initially switch 'S' is closed. After sometime 'S' is left open and dielectric slabs of dielectric constant K = 3 are inserted to fill completely the space between the plates of the two capacitors. How will the (i) charge and (ii) potential difference between the plates of the capacitors be affected after the slabs are inserted?

View SolutionFigure shows two identical capacitors C1andC2 each of 2μF capacitance, connected to a battery of 5 V. Initially switch 'S' is closed. After some time 'S' is left open and dielectric slavs of dielectric constant K = 5 are inserted to fill completely the space between the plates of the two capacitors. How will the (i) charge and (ii) potential difference between the plates of the capacitors be affected after the slabs are inserted?
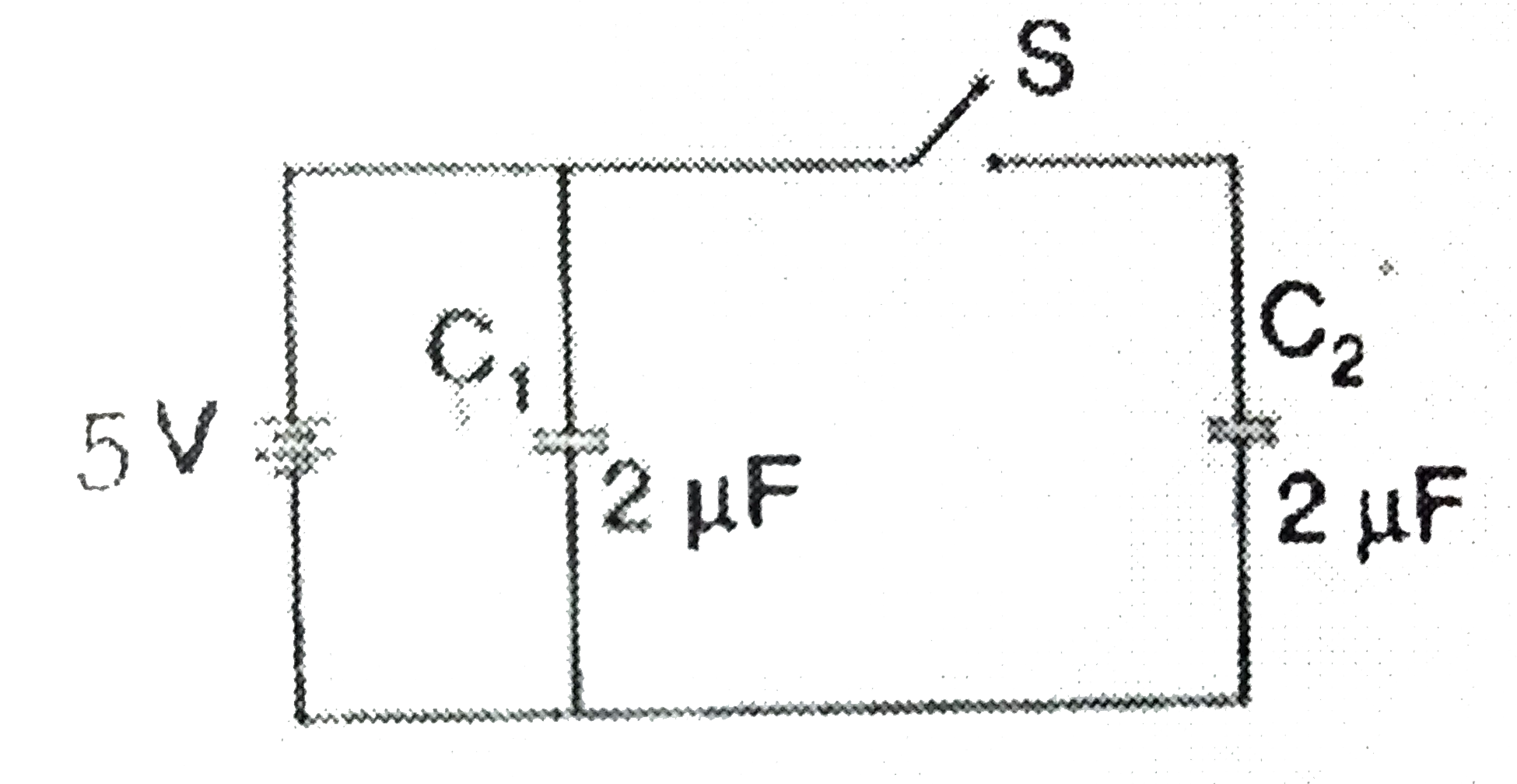
View SolutionFigure shows two identical capacitors C1andC2 each of 2μF capacitance, connected to a battery of 5 V. Initially switch 'S' is closed. After some time 'S' is left open and dielectric slavs of dielectric constant K = 5 are inserted to fill completely the space between the plates of the two capacitors. How will the (i) charge and (ii) potential difference between the plates of the capacitors be affected after the slabs are inserted?

View SolutionFigure shows two identical caoacitors C1andC2 each of 1.5μF caoacitance, connected to a battery of 2 V. Initially switch 'S' is closed. After some time 's' is left open and dielectric slabs of dielectric constant K=2 are inserted to fill completely the space between the plates of the two capacitors. How will the (i) charge and (ii) potential difference between the plates of the capacitors be affected after the slabs are inserted.
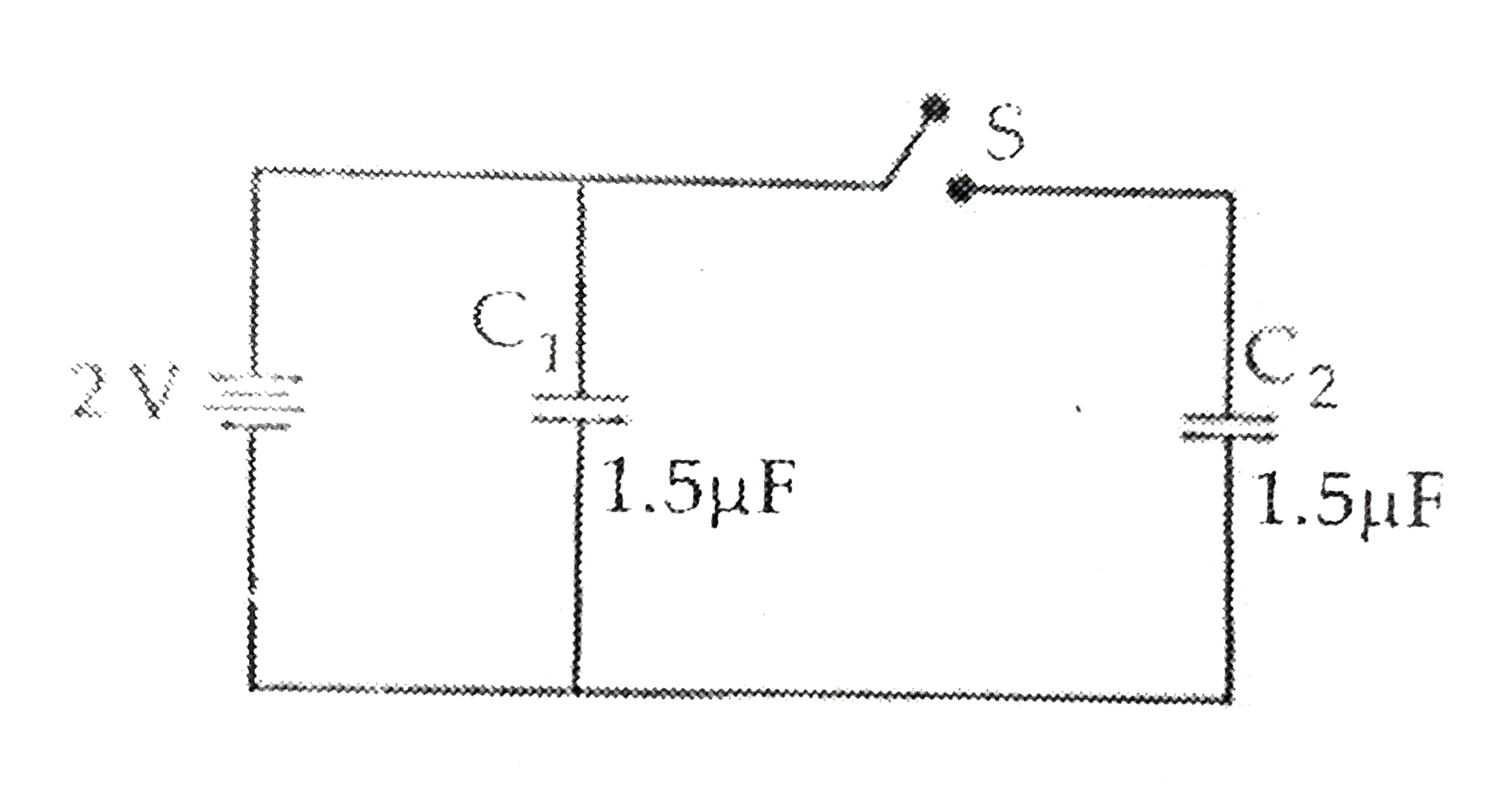
View Solution
