A parallel-plate capacitor is filled with a delectric meterial having resistivity(ρ)and dielectric constant K.The capcitor is charged and disconnected from the charging source. The capacitor is slowly discharged through the dielectric.Show that the time constant of the discharge is independent of all gepmetrical parameters like the plate area or separation between the plates. Find this time constant.
To solve the problem, we need to derive the time constant for the discharge of a parallel-plate capacitor filled with a dielectric material. Let's go through the steps systematically.
Step 1: Understand the Capacitor's Charge Equation
When the capacitor is charged and then disconnected from the charging source, the charge Q on the capacitor at any time t during discharge can be expressed as:
Q(t)=Q0e−t/(RC)
where Q0 is the initial charge, R is the resistance through which the capacitor discharges, and C is the capacitance of the capacitor.
Step 2: Determine the Capacitance with Dielectric
The capacitance C of a parallel-plate capacitor filled with a dielectric material is given by:
C=K⋅A⋅ϵ0d
where:
- K is the dielectric constant,
- A is the area of the plates,
- ϵ0 is the permittivity of free space,
- d is the separation between the plates.
Step 3: Determine the Resistance
The resistance R of the dielectric material can be expressed in terms of its resistivity ρ:
R=ρ⋅dA
where:
- ρ is the resistivity of the dielectric,
- d is the thickness of the dielectric,
- A is the area of the plates.
Step 4: Substitute Capacitance and Resistance into the Time Constant
The time constant τ for the discharge of the capacitor is given by:
τ=R⋅C
Substituting the expressions for R and C:
τ=(ρ⋅dA)⋅(K⋅A⋅ϵ0d)
Now simplifying this expression:
τ=ρ⋅d⋅K⋅A⋅ϵ0d⋅A
The d and A cancel out:
τ=ρ⋅K⋅ϵ0
Step 5: Conclusion
The final expression for the time constant τ is:
τ=ρ⋅K⋅ϵ0
This shows that the time constant is independent of the geometrical parameters such as the plate area A and the separation d.
When the capacitor is charged and then disconnected from the charging source, the charge Q on the capacitor at any time t during discharge can be expressed as:
Q(t)=Q0e−t/(RC)
where Q0 is the initial charge, R is the resistance through which the capacitor discharges, and C is the capacitance of the capacitor.
The capacitance C of a parallel-plate capacitor filled with a dielectric material is given by:
C=K⋅A⋅ϵ0d
where:
- K is the dielectric constant,
- A is the area of the plates,
- ϵ0 is the permittivity of free space,
- d is the separation between the plates.
The resistance R of the dielectric material can be expressed in terms of its resistivity ρ:
R=ρ⋅dA
where:
- ρ is the resistivity of the dielectric,
- d is the thickness of the dielectric,
- A is the area of the plates.
The time constant τ for the discharge of the capacitor is given by:
τ=R⋅C
Substituting the expressions for R and C:
τ=(ρ⋅dA)⋅(K⋅A⋅ϵ0d)
Now simplifying this expression:
τ=ρ⋅d⋅K⋅A⋅ϵ0d⋅A
The d and A cancel out:
τ=ρ⋅K⋅ϵ0
The final expression for the time constant τ is:
τ=ρ⋅K⋅ϵ0
This shows that the time constant is independent of the geometrical parameters such as the plate area A and the separation d.
Topper's Solved these Questions
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - questions for short answer
17 Videos
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - objective 2
9 Videos
- DISPERSION AND SPECTRABOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer
6 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer
6 Videos
Similar Questions
A parallel - plate capacitor, filled with a dielectric of dielectric constant k, is charged to a potential V0. It is now disconnected from the cell and the slab is removed. If it now discharges, with time constant τ, through a resistance, then find time after which the potential difference across it will be V0?
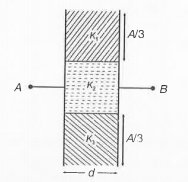
View SolutionA parallel plate capacitor of plate area A and separation d filled with three dielectric materials as show in figure. The dielectric constants are K1, K2 and K3 respectively. The capacitance across AB will be :
View SolutionA charged capacitor is discharged through a resistance. The time constant of the circuit is η. Then the value of time constant for the power dissipated through the resistance will be
View SolutionA parallel plate capacitor has a dielectric (of dielectric constant k) between the plates. The plates are charged to a surface charge density σ0. What is the density of the polarized charge that appear on the surface of the dielectric.
View SolutionA parallel plate capacitor with air as dielectric is charged to a potential .v. using a battery . Removing the battery. The charged capacitor is then connected across an identical uncharged parallel plate capacitor filled with was of dielectric constant k. The common potential of both the capacitor is
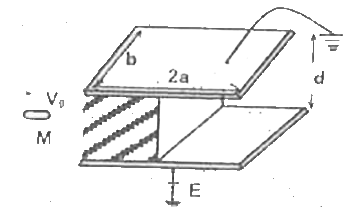
View SolutionA parallel plate capacitor is half filled with a dielectric slab of dielectric constant (K) and mass M. Capacitor is connected to a cell of e.m.f. E. Plates are held fixed on horizontal surface. A bullet of mass M hits the dielectric elastically and it is found that the dielectric slab just leaves out the capacitor. Find the speed of the bullet?
View SolutionA parallel capacitor of capacitance C is charged and disconnected from the battery. The energy stored in it is E. If a dielectric slab of dielectric constant 6 is inserted between the plates of the capacitor then energy and capacitance will become.
View SolutionA parallel plate capacitor with square plates is filed with four dielectrics of dielectric constants K1,K2,K3,K4, arranged as shown in the figure. The effective dielectric constant K will be :
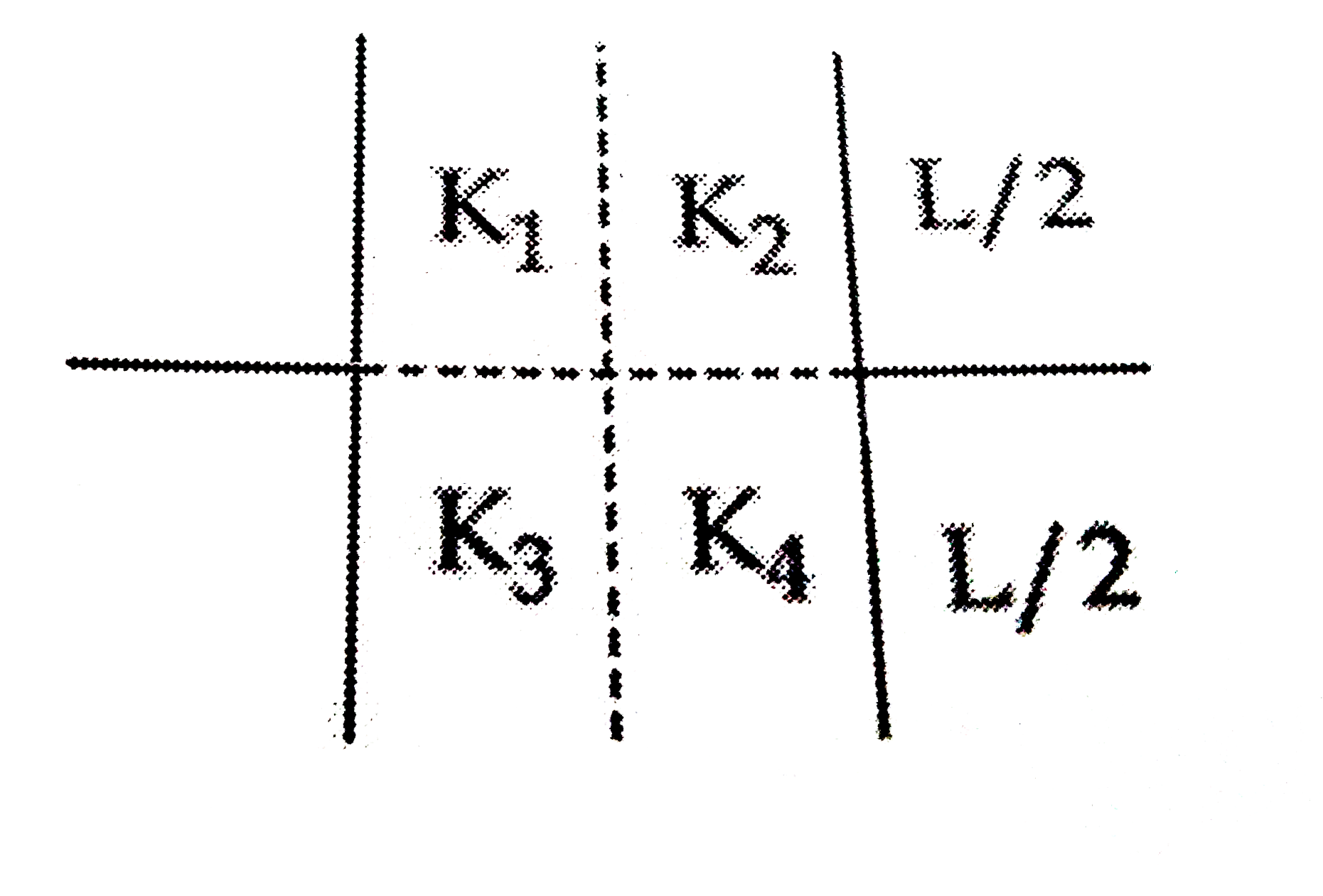
View SolutionA parallel plate capacitor with liquid filled between the plates (dielectric constant of liquid, k=4)has capacitance 20μF. If the liquid is removed then capacitance of capacitor becomes
View SolutionFind an expression for the capacitance of a parallel plate capacitor when a dielectric slab of dielectric constant K and thickness t=d2 but the same area on the plates is inserted between the the capacitors plate. (d=separation between the plates)
View Solution
