A parallel plate capacitor with circular plates of radius 1 m has a capacitance of 1 nF. At t = 0, it is connected for charging in series with a resistor R=1MO¬a across a 2V battery. Calculate the magnetic field at a point P, halfway between the centre and the periphery of the plates, after t=10−3s. (The charge on the capacitor at time t is q (t) = CV [1 - exp (−t/τ)], where the time constant τ is equal to CR.)
![A parallel plate capacitor with circular plates of radius 1 m has a capacitance of 1 nF. At t = 0, it is connected for charging in series with a resistor R = 1 M Onega across a 2V battery. Calculate the magnetic field at a point P, halfway between the centre and the periphery of the plates, after t=10^(-3)s. (The charge on the capacitor at time t is q (t) = CV [1 - exp (-t//tau)], where the time constant tau is equal to CR.)](https://d10lpgp6xz60nq.cloudfront.net/physics_images/KPK_AIO_PHY_XII_P1_C08_E02_001_Q01.png) Solution in Gujrati
Solution in Gujrati
Here, during charging of a capacitor, charge on its plate changes with time according to formula q=CV(1−e−t/RC). Hence surface charge density on the plate changes according to σ=qA. Hence electric field between the plates of a capacitor changes according to E=σ∈0. Because of this electric flux, associated with area A1=πr21 between the plates changes according to ΦE=A1E which gives rise to displacement current id=∈0dΦEdt. Because of this, we get induced magnetic field B whose magnitude can be obtained using Ampere - Maxwell law.
During the charging of a capacitor, charge on the plate of a capacitor at time t is given by q=q0(1−e−t/τ)
(Where q0=CV= maximum charge on the plate of a capacitor and τ=RC= time constant)
∴q=CV(1−e−t/RC)
∴q=CV−CVe−t/RC
∴dqdt=0−CVe−t/RC(−1RC)=VRe−t/RC ....(1)
(Where R = external resistance in the circuit)
At time t, displacement current enclosed by Amperean loop of radius r given by,
id=∈0dΦEdt
∴id=∈0ddt{A.E}
(Where A. = area enclosed by considered circular Amperean loop =πr2 and r = radius of this loop)
∴id=∈0ddt{πr2×σ∈0}
(Where σ= surface charge density on the plate of a capacitor)
∴id=πr2ddt(σ)
=πr2ddt(qπR20)
(Where R0= radius of plate of a capacitor)
=(rR0)2dqdt
∴id=(rR0)2VRe−t/RC [From equ. (1)] ....(2)
Placing the respective values,
id=(0.51)2(21×106)(2.718)−(10−31×106×1×10−9)
∴id=14×2106×(2.718)
∴id=0.184×10−6A
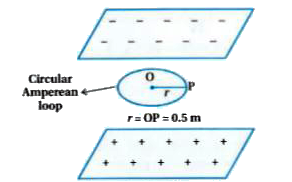
Now, as shown in the figure, because of above displacement current, magnitude of magnetic field at each point on the circumference of circular Amperean loop, considered between the plates of a capacitor, parallel to its plates will be same. If this magnitude is B then, according to Ampere - Maxwell, line integration of induced magnetic field, taken over loop will be,
∮→B.→dl=μ0(ic+id)
∴∫Bdlcos0∘=μ0(0+id) (∵ In the region between the plates ic=0 and →B||→dl)
∴B∫dl=μ0id
∴B(2πr)=μ0id
∴B=μ0id2πr ...(3)
=4π×10−70.184×10−62π×0.5
∴B=0.736×10−3T
Topper's Solved these Questions
- ELECTROMAGNETIC WAVESBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - SECTION B NUMERICALS (Numerical From Textual Exercise)
35 Videos
- ELECTROMAGNETIC WAVESBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - SECTION B NUMERICALS (Numerical From .DARPAN. Based On Textbook)
12 Videos
- ELECTROMAGNETIC WAVESBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - SECTION A QUESTIONS - ANSWERS (TRY YOURSELF)
45 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D MCQs (MCQs asked in Competitive Exams )
38 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - KUMAR PRAKASHANCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Section D ( MCQs asked in Cometitive Exams )
39 Videos
Similar Questions
Figure shows a capacitor made of two circular plates each of radius 12 cm, and separated by 5.0 cm. The capacitor is being charged by an external source (not shown in the figure). The charging current is constant and equal to 0.15 A.
Calculate the capacitance and the rate of change of potential difference between the plates.
View SolutionThe maximum electric field at a distance of 10m from an isotropic point source of light is 3.0Vm−1. Calculate (a) the maximum value of magnetic field, (b) average intensity of light at that place and (c ) the power of the source. [c=3×108ms−1,ε0=8.854×10−12C2N−1m−2]
View SolutionAccording to Maxwell which is missing term in Maxwell's - Ampere circuital law ?
View SolutionThree pure inductance each of 3 H are connected as shown in figure. The equivalent inductance of this connection between points A and B is ......

View SolutionCapacitance of a capacitor 100 μ F. The work is done for depositing chargc 8×10−18 C on it will be .........
View SolutionA parallel plate capacitor with circular plates of radius 1m has a capacitance of 0.5muF. At t=0, it is connected for charging inseries with a resistance R=2kOmega across a 4V battery. Calculate the magnetic field at a point P in between the plates and half way between the centre and periphery of the plates after 10^-3s . Fig.
View SolutionA parallel plate capacitor has an electric field of 10^(5)V//m between the plates. If the charge on the capacitor plate is 1muC , then force on each capacitor plate is-
View SolutionA parallel plate capacitor with circular plates of radius 1m has a capacitor of 1nF . At t = 0 , it is connected for charging in series with a resistor R = 1MOmega across a 2V battery. Calculate the magnetic field at a point P , halfway between the cnetre and the periphery of the plates, after t = 10^(-3)sec .
View SolutionA parallel plate capacitor with circular plates of radius 1m has a c apacitance of 1n F. At t=0,it is connected for charging in series with a resistance R=1MΩ across2V battery . Calculate the magnetic field at a point P, in between the plates and half way between the centre and the periphery of the plates after 10−3s.
View Solutionएक समांतर प्लेट संधारित्र जिसकी व्रत्ताकार प्लेटों की त्रिज्या 1m है धारिता 1nf है। समय t = 0 पर इसको आवेशित करने के लिए R= 1 MΩ के एक प्रतिरोधक के साथ श्रेणीक्रम में 2V की बैटरी से जोडा गया है (चित्र 8.3) । 10−3s ds पश्चात संधारित्र के बीच में दोनों प्लेटों के केंद्र एवं उनकी परिमिति के ठीक मध्य में स्थित बिंदु P पर चुंबकीय क्षेत्र का परिकलन कीजिए । [क्षण t पर संधारित्र पर आवेश q(t)=CV[1–exp(−t/π)] होता है जहाँ समय नियतांक τ=CR है ]।

View Solutionकिसी समांतर प्लेट संधारित्र की वृत्ताकार प्लेटो की त्रिज्या 1 m तथा धारिता C=1nF है। इसे चित्र 1।9 के अनुसार 2 V की बैटरी तथा 1MΩ के एक प्रतिरोधक के साथ श्रेणीक्रम में जोड़ा गया है। आवेशित करने के लिए सलंगन स्विच को समय t = 0 पर बंद किया जाता है समय t=1ms पर संधारित्र के बीच में दोनों प्लेटो के केंद एव उसकी परिमिति के ठीक माध्य में स्थति बिंदु P पर चुंबकीय क्षेत्र का मान ज्ञात करे। मान ले कि आवेशन के क्रम संधारित्र पर आवेश का तात्कालिक मान है- q(t)CV(1−etCR)
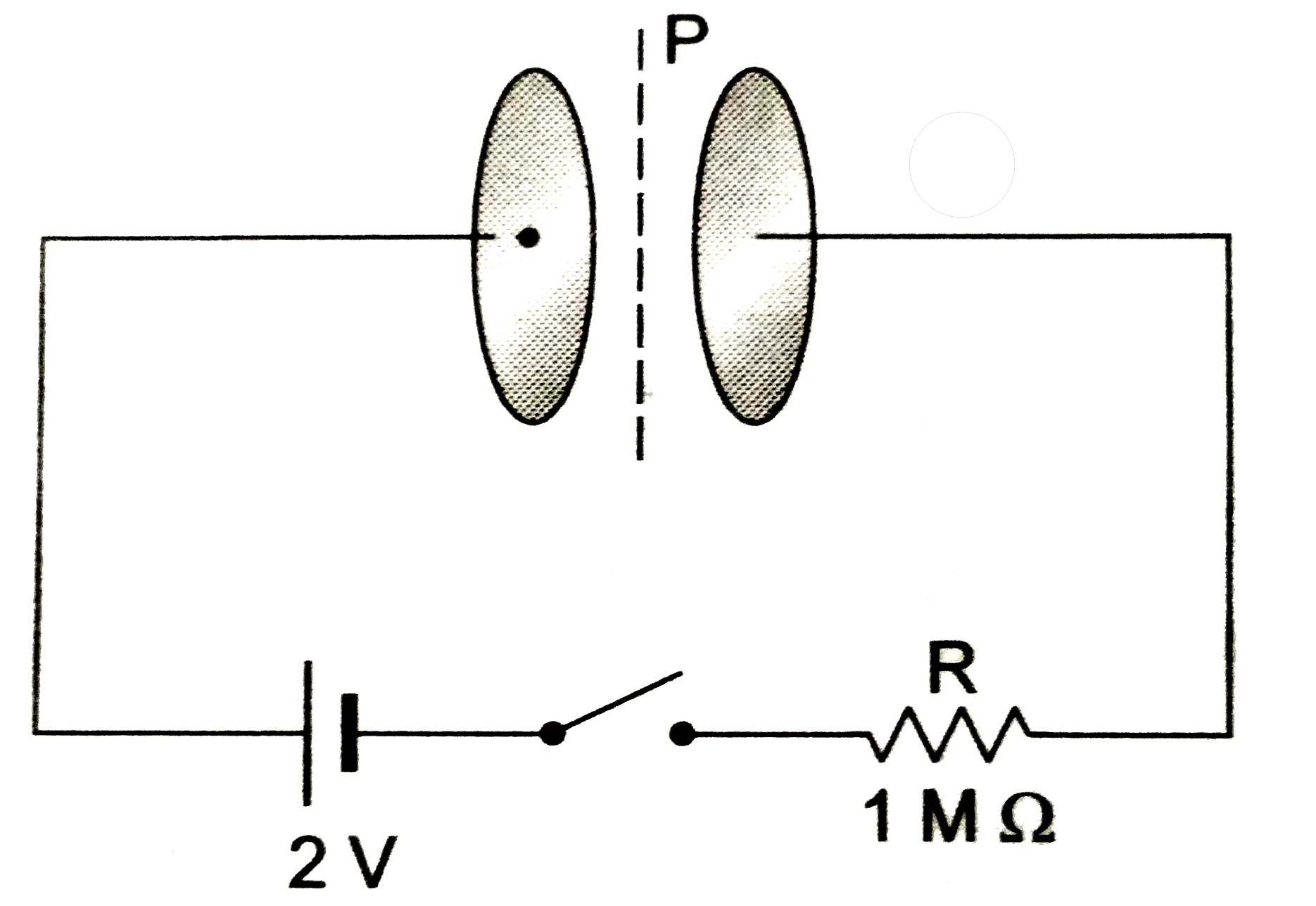
View SolutionA parallel plate capacitor with circular plates of radius 1m has a capacitance of 1 nF. At t=0 , It is connected for charging in series with are resistor R=1 M Q across a 2V battery (fig). Calculate the magnetic field at a point P halfway between the centre and the periphery of the plates. after t=10−3s. (The charge on the capacitor at time τ is q(t) CV [1 =exp (−t/τ) ], where the time constant τ is equal to CR).
View SolutionA parallel plate capacitor has an electric field of 10^(5)V//m between the plates. If the charge on the capacitor plate is 1muC , the force on each capacitor plate is
View Solutionएक समांतर प्लेट संधारित्र जिसकी वृताकार प्लटो की त्रिज्या 1m है धारिता 1nF है समय t =0 पर इसको आवेशित करने के लिए R=1MΩ के एक प्रतिरोधक के साथ श्रेणीक्रम में 2V की बैटरी से जोड़ा गया है ( चित्र ) 10−3S के पश्चात संधारित्र के बीच में दोनों प्लेटो के केंद्र एवं परिकलन कीजिए [क्षण t पर संधारित्र पर आवेश q(t)=CV[1−exp(−t/t) होता है जहाँ समय नियतांक τ=CR है
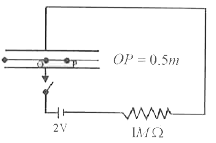
View SolutionA parallel plate capacitor with circular plates of radius 1m has a capacitance of 1nF. At t = 0, it is connected for chargeing in series with a resistor R=1 M Omega across a 2V battery (Figure). Calculate the magnetic field at a point P, halfway between the centre and the periphery of the plates, after t=10^(-3)s . (The charge on the capacitor at time t is q(t)=CV[1-exp((-t)/(tau))] , where the time constant tau is equal to CR).
View Solution
