A particle a having a charge of 5.0×10−7C is fixed in. a vertical wall. A second particle B of mass 100 g and. having equal charge is supended by a silk thread. of length 30 cm form the wall. The point of suspension is. 30 cm above the particle A. Find the angle of the thread. with the vertical when it stays in equilibrium. Solution in Tamil

The situation is shown in figure . Supppose the
piont suspension is O and let theta be the angle between
the thread and the vertical. Forces on the particle B are
(i) weight mg downward
(ii) tension T along the thread and
(iii) electric force of repulsion F along AB.
For equilibrium, these forces should add to zero. Let
X'' BX be the line perpendicular to OB. we shall take the
components of the forces along BX. This will giva a
relation between F, mg and θ
The verious andgles are shown in the figure. As
OA=OB,∠OAB= 90^@ - (theta)/(2)<br>Theother∠scanbewritendowndirectly.<br>Tak∈gcompo≠ntsalongBX,we≥t<br>F cos (theta) /(2) = mg cos ( 90^@ - theta)<br>= 2 mg sin (theta)/(2) cos (theta)/(2)<br>or,sin (theta)/(2) = (F)/ (2mg)<br>Now, F = (9xx10 ^9 Nm^2 C^(-2) xx (5.0 xx 10 ^(-7) C)^2 xx (1)/(AB^2)<br>andAB = 2 (OA) sin (theta)/(2).<br>Thus,F = (9 xx 10 ^9 xx 25 xx 10(-14))/(4 xx (30xx10^(-2))^2 xx sin^2. (theta)/(2)) N<br>om(i)and(ii),<br>sin (theta)/(2) = (F )/(2 mg) = (9xx 10^9 xx 25 xx 10 ^(-14) N )/(4xx ( 30 xx 10 ^(-2)^2 xx sin^2 .(theta)/(2)) . (1)/(2mg) or
sin3(θ)2=9×109×25×10−14N4×9×10−2×2×(100×10−3kg)×9.8ms(−2)
=0.0032
or sin (theta)/(2) = 0.15, giving theta =17^@.
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - question for short answer
14 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 1
9 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises
75 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMACHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Exercise
23 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE
98 Videos
Similar Questions
The charge on a proton is +1.6X10(−19)C and that on an
. electron is −1.6X10(−19)C. Does it mean that the electron
. has a charge 3.2X10(−19)c less than the charge of a
. proton?
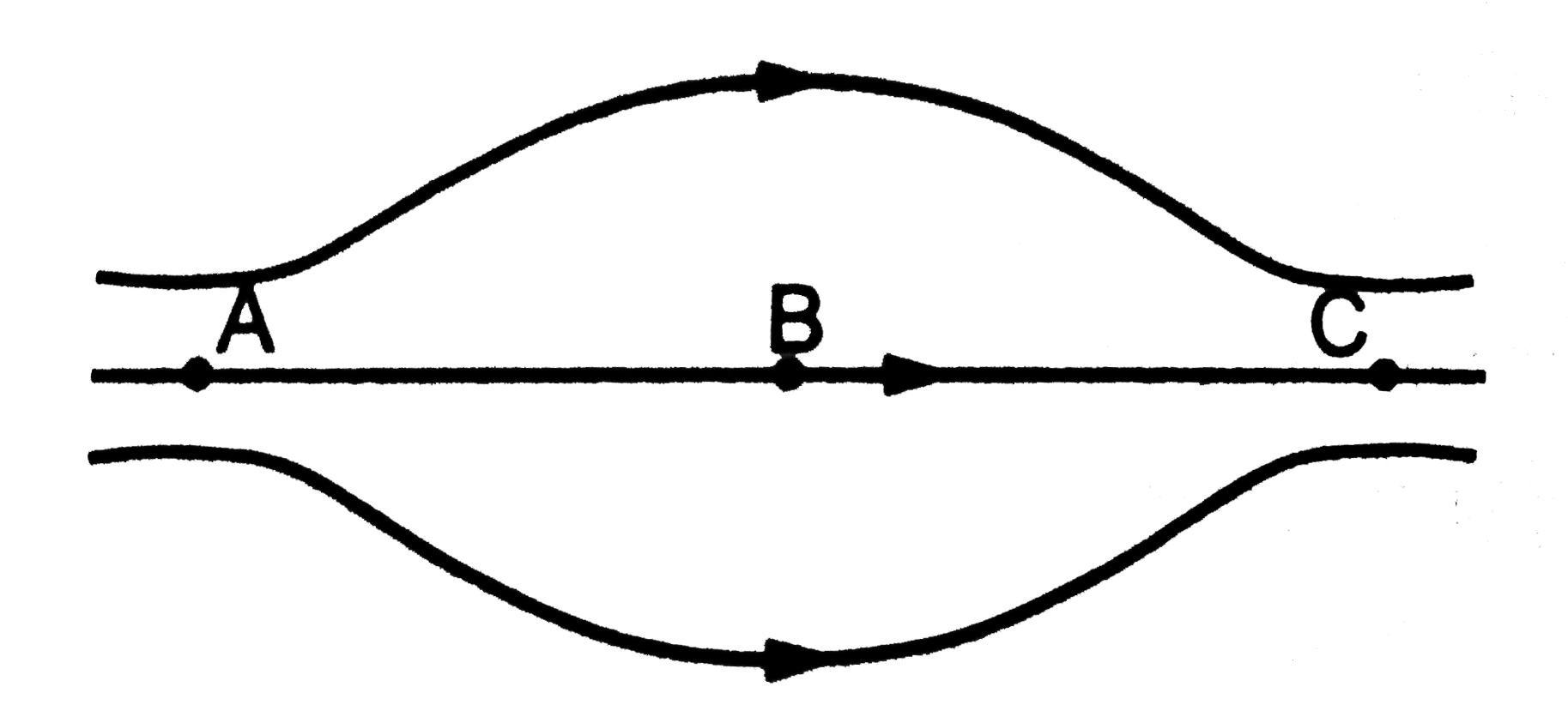
View SolutionFigure shows some of the electric field lines correspoinding to an electric field. The figure suggests that
View SolutionFind the dimensional formula of ε0 .
View SolutionA discharge tube contains helium at a low pressure. A large potential difference is applied across the tube. Consider a helium atom that has just been ionized due to the detachment of an atomic electron. Find the ratio of the distance travelled by the free electron to that by the positive ion in a short time dt after the ionization.
View SolutionCalculate the dimensions of (a) ∫→E.d→l,(b)vBlanddΦ0dt. The symbols have their usual meanings.
View SolutionA Charged particle of mass 1.0 g is suspended through a
. silk thread of length 40 cm in a horizantal electric field
. of 4.0×104NC−1 . If the particle stays aty a distance of
. 24 cm from the wall in equilibrium, find the charge on
. the particle.
View SolutionOne end of a 10 cm long silk thread is fixed to a large vertical surface of a xharged nonconducting plate and the other end is fastened to a small ball having a mass of 10 g and charge of 4.0×10C. In equilibrium, the thread make an angle of 600 with the vertical. Find the surface charge dendity on the plate.
View SolutionA simple pendulum of mass m and charge +q is suspended vertically by a massless thread of length l. At the point of suspension, a point charge +q is also fixed. If the pendulum is displaced slightly from equilibrium position, its time period will be
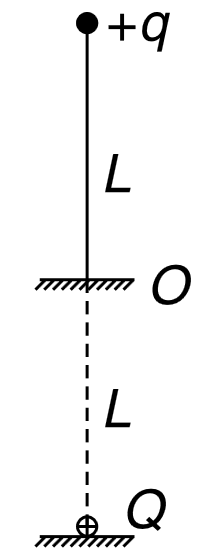
View SolutionA particle of mass m and charge q is attached to a light insulating thread of length L. The other end of the thread is secured at point O. Exactly below point O, there is a small ball having charge Q fixed on an insulating horizontal surface. The particle remains in equilibrium vertically above the ball with the string taut. Distance of the ball from point O is L. Find the minimum value of Q for which the particle will be in a stable equilibrium for any gentle horizontal push given to it.
View SolutionBelow the fixed end O of the insulating horizontal thread OB, there is a fixed charge A of Q = 20muc . At the end B of the thread there is a small mass m carrying charge Q = 20moc . The mass is released from the position shown and it is found to come to rest when the thread becomes vertical. Assume that the thread does not hit the fixed charge at A. [g = 10 m//s^2] (a) Find mass m. (b) Find tension in the thread in the equilibrium position when the thread is vertical. (c) Is the equilibrium mentioned in (b) stable or unstable?
View SolutionA particle of mass m and charge q is suspended from a point A with a silk thread of length l. Another particle of charge -q is fixes at a distance I from the point A such that point A and the charge -q lie in same horizontal plane. If at equilibrium , the thread makes angle 30^(@) with vertical, find the mass m and tension in the thread . ( Take acceleration due to gravity as g).
View SolutionA particle A having a charge of 5.0×10−7C is fixed in a vertical wall. A second particle B of mass 100g and having equal charge is suspended by a silk thread of length 30 cm from the wall. The point of suspension is located 30 cm vertically above the first particle. Find the angle of the thread with the vertical when it stays in equilibrium.
View Solution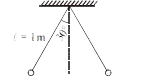
दो गेंदें जिनमें प्रत्येक का द्रव्यमान 1 gm है 1 m लम्बाई के कुचालक धागों की सहायता से निलम्बित किया गया है। संतुलन में धागे तथा ऊर्ध्वाधर इ मध्य कोण 30∘ है। किसी एक गेंद पर आवेश ज्ञात करे -
View SolutionA Charged particle of mass 1.0 g is suspended through a
. silk thread of length 40 cm in a horizantal electric field
. of 4.0×104NC−1 . If the particle stays aty a distance of
. 24 cm from the wall in equilibrium, find the charge on
. the particle.
View SolutionOne end of a 10 cm long silk thread is fixed to a large vertical surface of a charged non conducting plate and the other end is fastened to a small ball having a mass of 10 g and charge of 4.0×10C. In equilibrium, the thread make an angle of 600 with the vertical. Find the surface charge density on the plate.
View SolutionOne end of a 10 cm long silk thread is fixed to a large vertical surface of a charged non-conducting plate and the other end is fastened to a small ball of mass 10 g and charge of 4×10−6C. In equilibrium, thread makes an angle of 60o with the vertical.
(a) Find the tension in the string in equilibrium.
(b) Suppose the ball is slightly pushed aside and released. Find the time period of the small oscillations.
(Use σ=7.5×10−7Cm2)
View Solution
