One end of a 10 cm long silk thread is fixed to a large vertical surface of a charged non-conducting plate and the other end is fastened to a small ball of mass 10 g and charge of 4×10−6C. In equilibrium, thread makes an angle of 60o with the vertical.
(a) Find the tension in the string in equilibrium.
(b) Suppose the ball is slightly pushed aside and released. Find the time period of the small oscillations.
(Use σ=7.5×10−7Cm2)
To solve the problem step by step, we will break it down into two parts as specified in the question.
Part (a): Finding the Tension in the String
1. Identify Given Values:
- Length of the thread (L) = 10 cm = 0.1 m
- Mass of the ball (m) = 10 g = 10 × 10^(-3) kg = 0.01 kg
- Charge of the ball (Q) = 4 × 10^(-6) C
- Angle with the vertical (θ) = 60°
- Surface charge density (σ) = 7.5 × 10^(-7) C/m²
- Acceleration due to gravity (g) = 10 m/s²
2. Draw a Free Body Diagram:
- The forces acting on the ball are:
- Weight (W) acting downwards: W=mg
- Tension (T) in the thread acting at an angle θ with the vertical.
3. Resolve the Tension into Components:
- Vertical component of tension: Tcos(θ)
- Horizontal component of tension: Tsin(θ)
4. Set Up the Equations:
- In equilibrium, the vertical component of tension balances the weight of the ball:
Tcos(60°)=mg
- Substitute cos(60°)=12:
T⋅12=mg
- Rearranging gives:
T=mgcos(60°)=mg12=2mg
5. Calculate the Tension:
- Calculate mg:
mg=0.01kg×10m/s2=0.1N
- Therefore,
T=2×0.1N=0.2N
Part (b): Finding the Time Period of Small Oscillations
1. Identify the Forces:
- The weight of the ball acts downwards.
- The electrostatic force (F_e) acts horizontally due to the charged plate.
2. Calculate the Electrostatic Force:
- The electric field (E) due to the charged plate is given by:
E=σϵ0
- Where ϵ0=8.85×10−12C2/N m2.
- Therefore,
E=7.5×10−78.85×10−12≈8.47×104N/C
3. Calculate the Electrostatic Force:
- The force on the ball due to the electric field is:
Fe=QE=(4×10−6C)(8.47×104N/C)≈0.3388N
4. Determine the Effective Acceleration:
- The net force acting on the ball when displaced is given by:
Fnet=√(mg)2+(Fe)2
- The acceleration (a) can be expressed as:
a=Fnetm
5. Calculate the Time Period:
- The time period T of small oscillations is given by:
T=2π
⎷Lg+Fem
- Substitute the values:
T=2π
⎷0.110+0.33880.01
- Calculate:
T≈2π√0.110+33.88=2π√0.143.88≈0.45s
Final Answers:
- (a) The tension in the string is 0.2 N.
- (b) The time period of small oscillations is approximately 0.45 seconds.
- Length of the thread (L) = 10 cm = 0.1 m
- Mass of the ball (m) = 10 g = 10 × 10^(-3) kg = 0.01 kg
- Charge of the ball (Q) = 4 × 10^(-6) C
- Angle with the vertical (θ) = 60°
- Surface charge density (σ) = 7.5 × 10^(-7) C/m²
- Acceleration due to gravity (g) = 10 m/s²
- The forces acting on the ball are:
- Weight (W) acting downwards: W=mg
- Tension (T) in the thread acting at an angle θ with the vertical.
- Vertical component of tension: Tcos(θ)
- Horizontal component of tension: Tsin(θ)
- In equilibrium, the vertical component of tension balances the weight of the ball:
Tcos(60°)=mg
- Substitute cos(60°)=12:
T⋅12=mg
- Rearranging gives:
T=mgcos(60°)=mg12=2mg
- Calculate mg:
mg=0.01kg×10m/s2=0.1N
- Therefore,
T=2×0.1N=0.2N
- The weight of the ball acts downwards.
- The electrostatic force (F_e) acts horizontally due to the charged plate.
- The electric field (E) due to the charged plate is given by:
E=σϵ0
- Where ϵ0=8.85×10−12C2/N m2.
- Therefore,
E=7.5×10−78.85×10−12≈8.47×104N/C
- The force on the ball due to the electric field is:
Fe=QE=(4×10−6C)(8.47×104N/C)≈0.3388N
- The net force acting on the ball when displaced is given by:
Fnet=√(mg)2+(Fe)2
- The acceleration (a) can be expressed as:
a=Fnetm
- The time period T of small oscillations is given by:
T=2π
⎷Lg+Fem
- Substitute the values:
T=2π
⎷0.110+0.33880.01
- Calculate:
T≈2π√0.110+33.88=2π√0.143.88≈0.45s
- (a) The tension in the string is 0.2 N.
- (b) The time period of small oscillations is approximately 0.45 seconds.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Short Question7videos
GAUSS LAW
- BOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Objective 28videos
GAUSS LAW
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise8videos
ELECTROMAGNETIC WAVES
- BOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer18videos
GEOMETRICAL OPTICS
Similar Questions
One end of a 10 cm long silk thread is fixed to a large vertical surface of a charged non conducting plate and the other end is fastened to a small ball having a mass of 10 g and charge of 4.0×10C. In equilibrium, the thread make an angle of 600 with the vertical. Find the surface charge density on the plate.
View SolutionA particle of mass 200 g , is whirled into a vertical circle of radius 80 cm uisig a massless string The speed of the particle when the string makes an angle of 60∘ with the vertical line is 1.5ms−1. The tension in the string at this position is
View SolutionIf a small sphere of mass m and charge q is hung from a silk thread at an angle θ with the surface of a vertical charged conducting plate, then for equilibrium of sphere, the surface charge density of the plate is
View SolutionIf a small sphere of mass m and charge q is hanged from a silk thread at an angle θ with the surface of a vertical charged conducting plate, then for equilibrium of sphere the surface charge density of the plate -
View SolutionOne end of a string 0.5m long is fixed to a point A and the other end is fastened to a small object of weight 8N. The object is pulled aside by a horizontal force F, until it is0.3m from the vertical through A.Find the magnitude of the tension T in the string and force F.
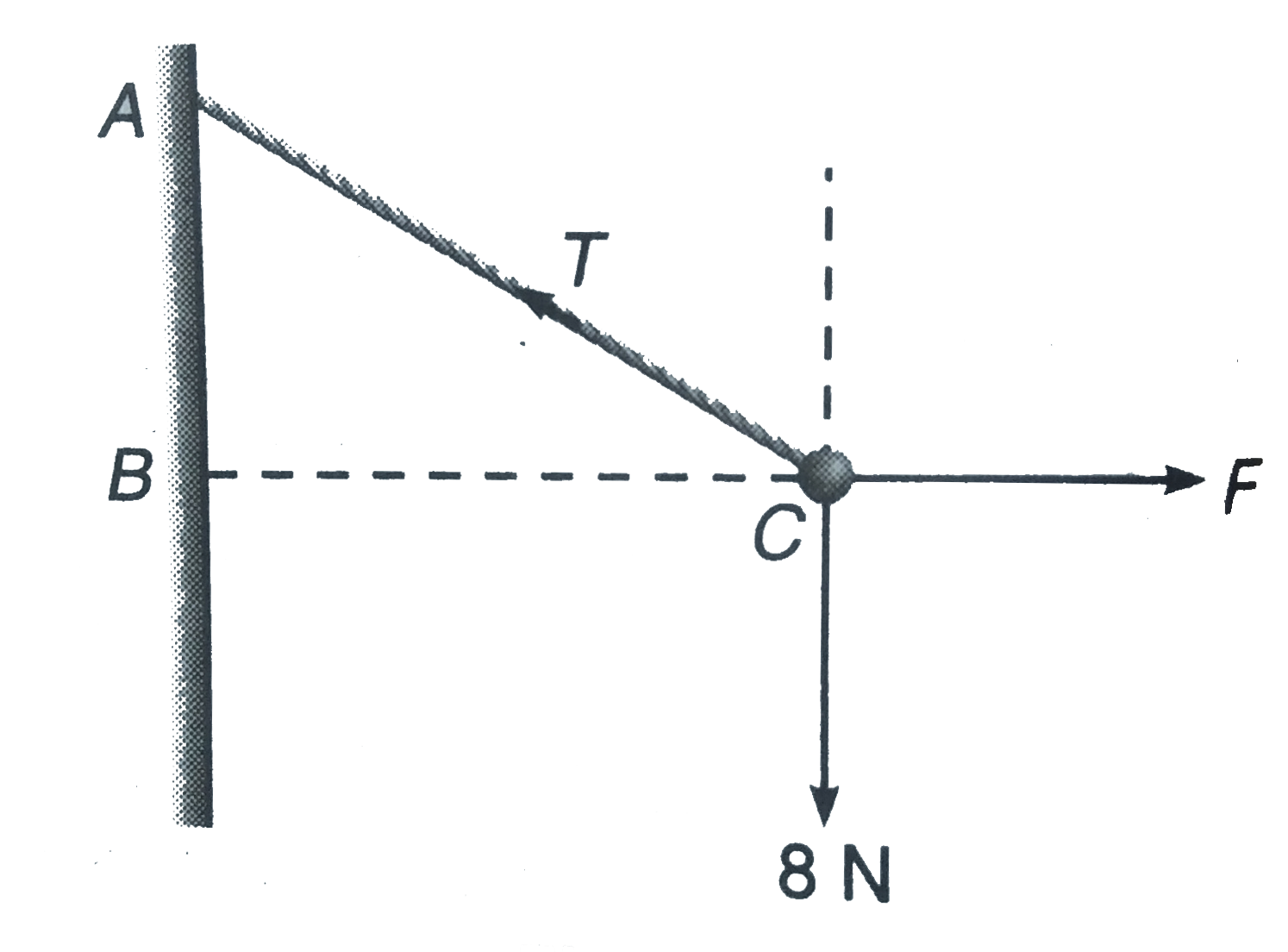 View Solution
View SolutionOne end of a string 0.5m long is fixed to a point A and the other end is fastened to a small object of weight 8N. The object is pulled aside by a horizontal force F, until it is0.3m from the vertical through A.Find the magnitudes of the tension T in the string and force F.
 View Solution
View SolutionA 1kg ball is suspended in a uniform electric field with the help of a string fixed to a point. The ball is given a charge √5 coulomb and the string makes an angle 37∘ with the vertical in equilibrium position. In the equilibrium position the tension is double the weight of the ball. Find the magnitude of the electric field in N/C.
View SolutionA small ball is suspended by a string from the ceiling of a car. As the car accelerates at a rate ‘a’ the string makes an angle '/theta' with the vertical in equilibrium. Then the tension in the string is :
View SolutionA mass M is suspended by a rope from a rigid support at A as shown in figure. Another rupe is tied at the end B, and it is pulled horizontally with a force. If the rope AB makes an angle θ with the vertical in equilibrium then the tension in the string AB is
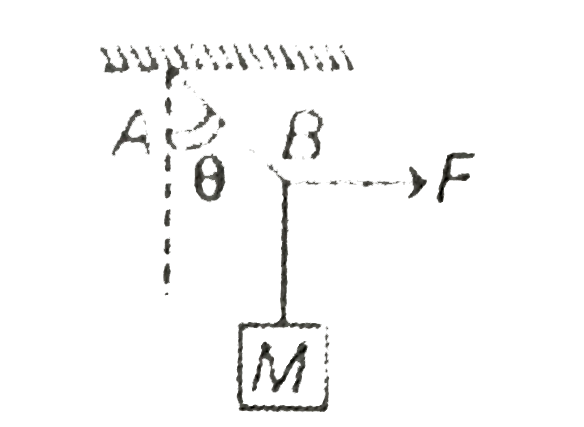 View Solution
View SolutionA particle of mass m and charge q is suspended from a point A with a silk thread of length l. Another particle of charge −q is fixes at a distance I from the point A such that point A and the charge -q lie in same horizontal plane. If at equilibrium , the thread makes angle 30∘ with vertical, find the mass m and tension in the thread . ( Take acceleration due to gravity as g).
View Solution

